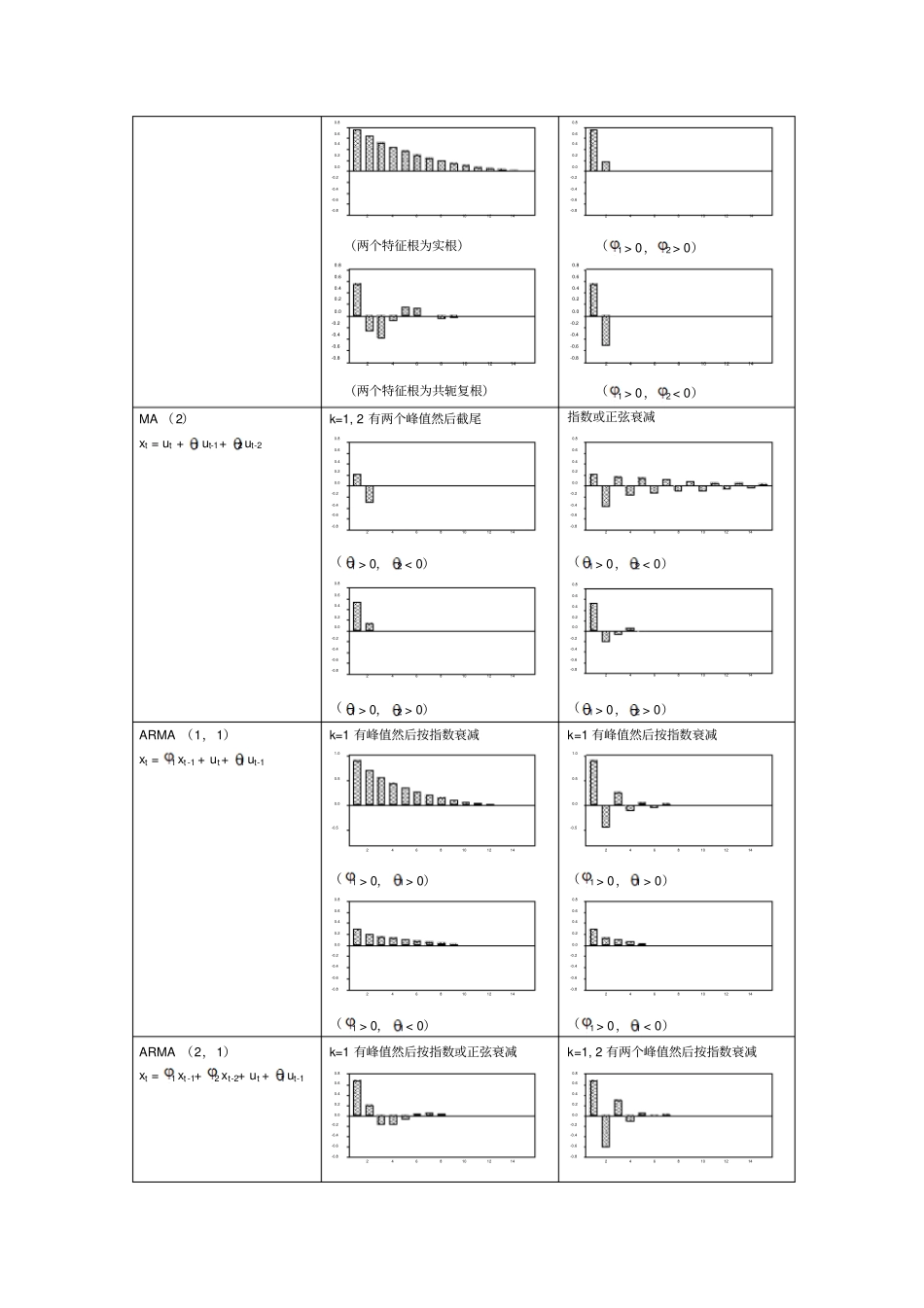
时间序列模型的构建和预测(BoxJenkinsMethodology)步骤1:识别。观察相关图和偏相关图步骤2:估计。估计模型中所包含的自回归系数和移动平均系数,可以用OLS来估计步骤3:诊断检验。选一个最适合数据的模型,检查从这模型中估计到的残差是否白噪声,如果不是的话,我们必须从头来过步骤4:预测。在很多情况下,这种方法得到的预测结果要比其它计量模型得到的要准确识别检查时间序列是否平稳-如果自相关函数衰退的很慢,则序列可能是非平稳-如果时间序列为一非平稳过程,应该运用差分的形式使它变为平稳过程-在检验了一个时间序列的平稳性之后,我们应该用相-0.8-0.6-0.4-0.20.00.20.40.60.82468101214-0.8-0.6-0.4-0.20.00.20.40.60.82468101214关图和偏相关图检验ARMA模型中的阶数p和q模型自相关函数特征偏自相关函数特征ARIMA(1,1,1)xt=1xt-1+ut+1ut-1缓慢地线性衰减AR(1)xt=1xt-1+ut若1>0,平滑地指数衰减若1<0,正负交替地指数衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214若11>0,k=1时有正峰值然后截尾若11<0,k=1时有负峰值然后截尾-0.8-0.6-0.4-0.20.00.20.40.60.82468101214MA(1)xt=ut+1ut-1若1>0,k=1时有正峰值然后截尾-0.8-0.6-0.4-0.20.00.20.40.60.82468101214若1<0,k=1时有负峰值然后截尾-0.8-0.6-0.4-0.20.00.20.40.60.82468101214若1>0,交替式指数衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214若1<0,负的平滑式指数衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214AR(2)xt=1xt-1+2xt-2+ut指数或正弦衰减k=1,2时有两个峰值然后截尾-1.0-0.50.00.51.02468101214-1.0-0.50.00.51.02468101214-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(两个特征根为实根)-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(两个特征根为共轭复根)-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2>0)-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2<0)MA(2)xt=ut+1ut-1+2ut-2k=1,2有两个峰值然后截尾-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2<0)-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2>0)指数或正弦衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2<0)-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2>0)ARMA(1,1)xt=1xt-1+ut+1ut-1k=1有峰值然后按指数衰减-0.50.00.51.02468101214(1>0,1>0)-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,1<0)k=1有峰值然后按指数衰减-0.50.00.51.02468101214(1>0,1>0)-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,1<0)ARMA(2,1)xt=1xt-1+2xt-2+ut+1ut-1k=1有峰值然后按指数或正弦衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214k=1,2有两个峰值然后按指数衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2<0,1>0)(1>0,2<0,1>0)ARMA(1,2)xt=1xt-1+ut+1ut-1+2ut-2k=1,2有两个峰值然后按指数衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,1>0,2<0)-0.8-0.6-0.4-0.20.00.20.40.60.81.02468101214(1>0,1>0,2>0)k=1有峰值然后按指数或正弦衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,1>0,2<0)-0.8-0.6-0.4-0.20.00.20.40.60.81.02468101214(1>0,1>0,2>0)ARMA(2,2)xt=1xt-1+2xt-2+ut+1ut-1+2ut-2k=1,2有两个峰值然后按指数或正弦衰减-0.6-0.4-0.20.00.20.40.62468101214(1>0,2<0,1>0,2<0)-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2<0,1>0,2>0)k=1,2有两个峰值然后按指数或正弦衰减-0.8-0.6-0.4-0.20.00.20.40.60.82468101214(1>0,2<0,1>0,2<0)-0.8-0.40.00.40.82468101214(1>0,2<0,1>0,2>0)●估计OLS方法在时间序列分析中的问题:■考虑下面简单的线性回归模型:ttteXZ■OLS估计量nttntttXZX121?为一致估计且为最优线性无偏估计量的条件为:0)(tteXE■但时间序列模型ttteZZ1中可能无法满足以上条件。它取决于误差项et的性质。■nttntttnttnttttnttntttZeZZeZZZZZ2212122121122121)(?■情形1:ttue■情形2:ttuLe)1(,2111))(()(utttttuuZEeZE极大似然估计法:■假设随机变量xt的概率密度函...