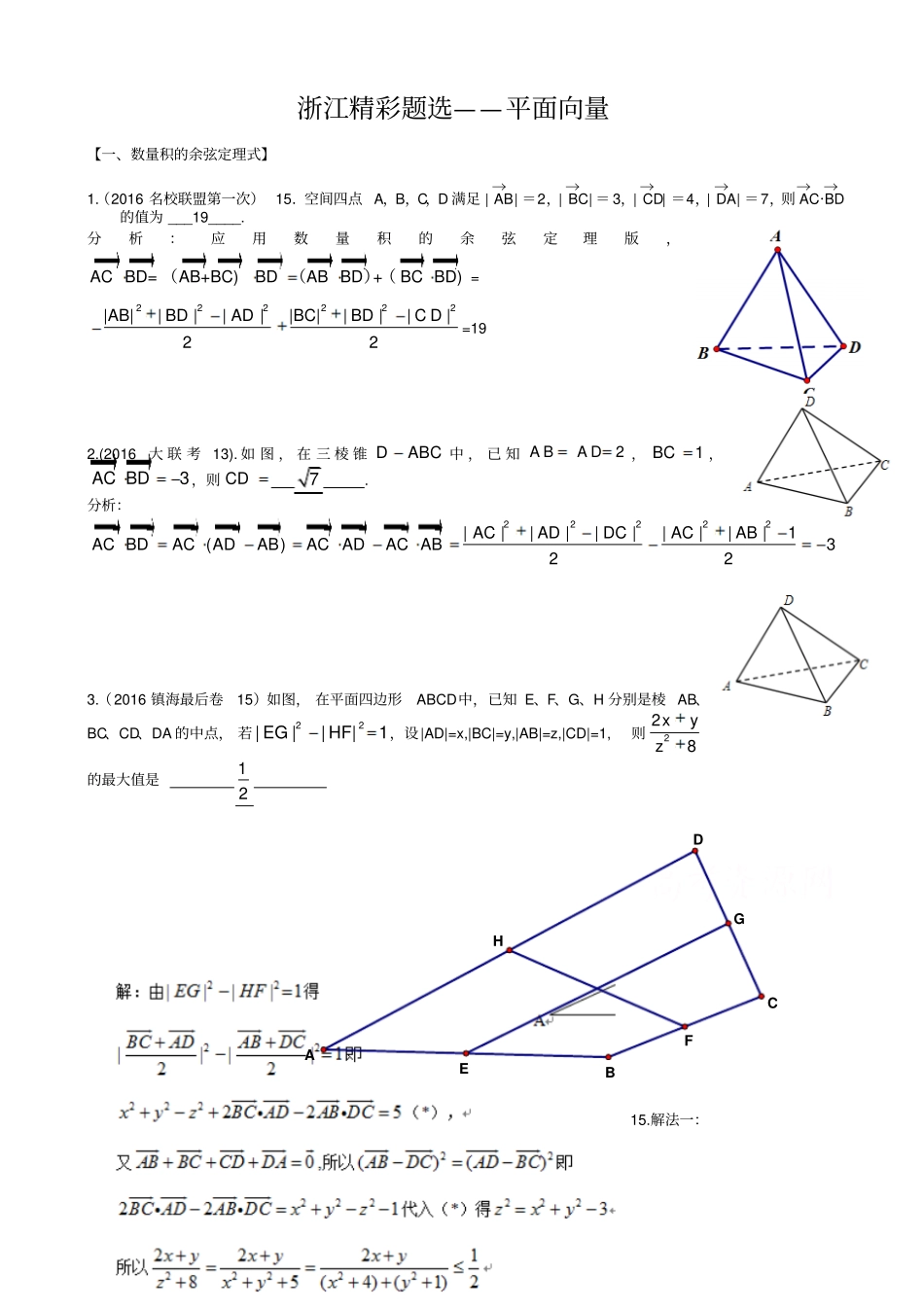
浙江精彩题选——平面向量【一、数量积的余弦定理式】1.(2016名校联盟第一次)15.空间四点A,B,C,D满足|→AB|=2,|→BC|=3,|→CD|=4,|→DA|=7,则→AC·→BD的值为___19____.分析:应用数量积的余弦定理版,ACBD=AB+BC)BDABBD+BCBD)(()(=222222|AB||||||BC||||C|22BDADBDD=192.(2016大联考13).如图,在三棱锥DABC中,已知2ABAD,1BC,3ACBD,则CD7.分析:22222||||||||||1()322ACADDCACABACBDACADABACADACAB3.(2016镇海最后卷15)如图,在平面四边形ABCD中,已知E、F、G、H分别是棱AB、BC、CD、DA的中点,若22|EG||HF|1,设|AD|=x,|BC|=y,|AB|=z,|CD|=1,则228xyz的最大值是1215.解法一:HGFEABCD解法二:设ACBD=O四边形EFGH为平行四边形22EGHF=22()()4EHEFEHEFEHEF()()BDACODOBOCOAODOCODOAOBOCOBOA=222||||||2ODOCDC222|||||A|2ODOAD222||||||2OBOCBC222|||||A|2OBOAB=22221(|DC||||DC||AB|)2AD=2221(y1)12xz2223zxy下同4.(2016杭二最后卷4)ABCΔ中,6,8==ACAB,AD垂直BC于点D,FE,分别为ACAB,的中点,若6=?DFDE,则=BCA.132B.10C.372D.14解:.A。由直角三角形可知,DE=AE,DF=AF,由数量积的余弦定理版可知,2222222||||||||||||169||6222DEDFEFAEAFEFEFDEDF则EF=13,所以BC=213【二、向量】1.(嵊州期末15).已知单位向量a,b的夹角为3,设向量xycab,x,yR,若1cab,则2xy的最大值为5.2.(2016浙江六校联考8)如图,在等腰梯形ABCD中,2AB,4CD,5BC,点E,F分别为AD,BC的中点。如果对于常数,在等腰梯形ABCD的四条边上,有且只有8个不同的点P使得PFPE成立,那么的取值范围是(C)A.(54,920)B.(920,114)C.(920,14)D.(54,114)分析:222||||||9PEPFPGGFPG,即的值为以G为圆心|PG|为半径的圆共与四边有八个交点。3.(2016丽水一模15)设非零向量ba,的夹角为,若存在Rm,使得向量2mab与mab的夹角也为,则cos的最小值是.EFABCDP(第8题图)4.(2016大联考6).P为△ABC内部一点,且满足||2||2PBPA,56APB,且2340PAPBPC,则ABC的面积为(A)A.98B.43C.1D.65分析:用0mPAnPBkPC则三个面积比为::kmn的结论5.(2016台州一模15)已知点C是线段AB上一点,CBAC2,MBMCMBMAMCMA,则2ABMBMA的最小值为29.分析:本题集中了向量中最时尚的元素,角平分线、极化恒等式、阿波罗尼斯圆。6.(2016绍兴二模13)在△ABC中,BC=6,G为△ABC的重心,BC的中垂线交AB于N,且6NGNCNGNB,则BABC36分析:投影,作图,可知A的投影在点C处。7.(2016嘉兴二模15)如图,设正△BCD的外接圆O的半径为)3321(RR,点A在BD下方的圆弧上,则ACADADABABAO)||||(的最小值为.解析:因为||||21)||()||||(2ACACACACACAOACADADABABAO21)1|(|212AC,因为RACR2||3,所以1||AC时,取到最小值21.8(2016温州二模15).如图,矩形ABCD中,3AB,4AD,,MN分别为线段,BCCD上的点,且满足22111CMCN,若ACxAMyAN,则xy的最小值为.分析:222222111CMCNCMCNCMCNMN边上的高|CH|=1;ACAExAMyAN,则xyAEAMAN,由共线定理得1xy即||55||5||4ACxyAECE点评:本题是一道精彩题,发现22111CMCN的内涵是关键,熟练用好爪形图是本质。9.(2016五校联考13题)已知向量,ab满足:2a,向量b与ab夹角为23则ab的取值范围是4343[2,2]33分析:画图,用投影。10.(2016新高考研究联盟二模13)已知ABC中,AB=8,BC=10,AC=6,P在平面ABC内内,且9PBPC,则||PA的取值范围[1,9]分析:2||259PBPCPD,||4PD,P点以D为圆心的圆。