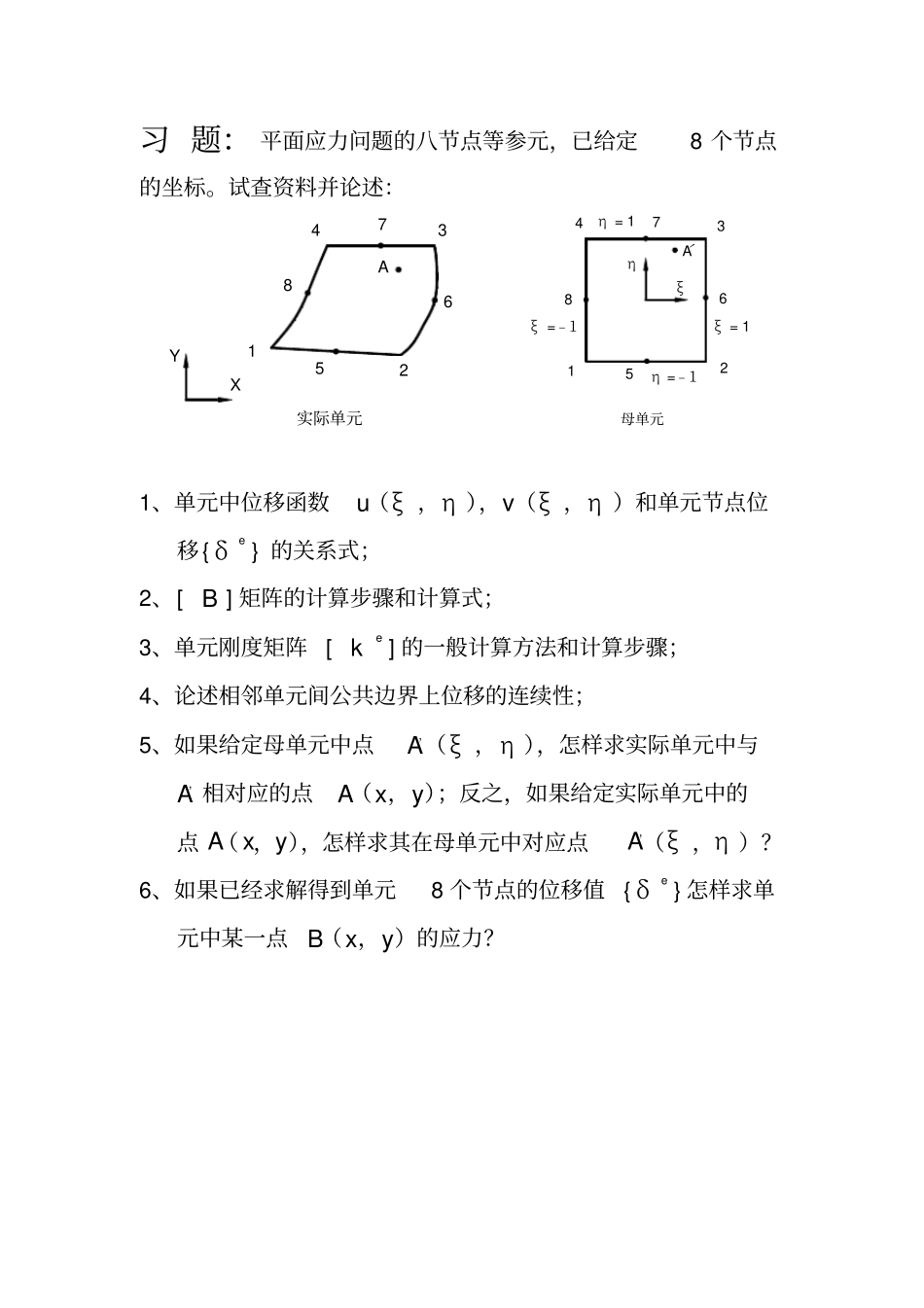
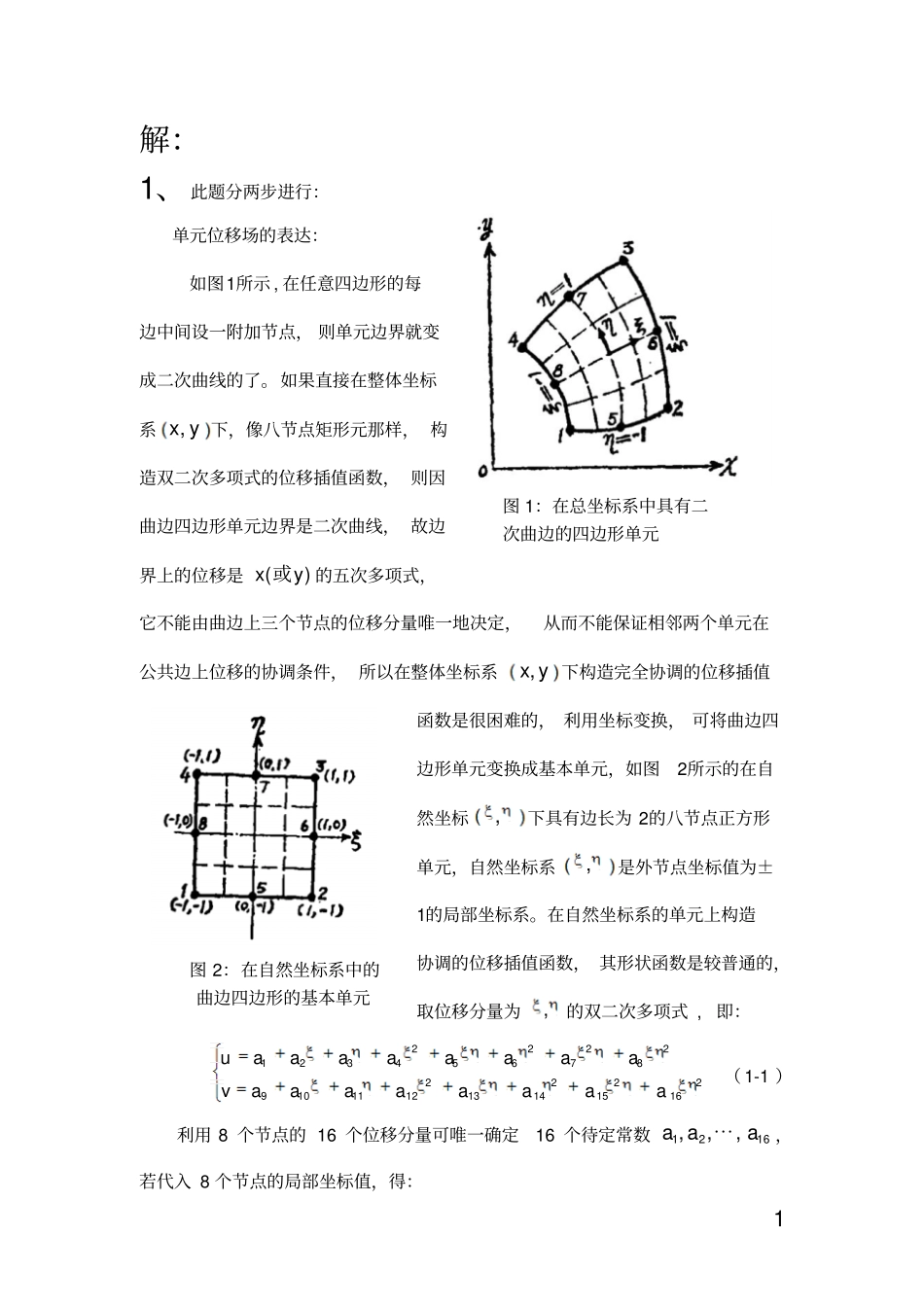
土木工程专业有限元第二次作业姓名:班级:学号:指导教师:二〇一五年6月12日习题:平面应力问题的八节点等参元,已给定8个节点的坐标。试查资料并论述:1、单元中位移函数u(ξ,η),v(ξ,η)和单元节点位移{δe}的关系式;2、[B]矩阵的计算步骤和计算式;3、单元刚度矩阵[ke]的一般计算方法和计算步骤;4、论述相邻单元间公共边界上位移的连续性;5、如果给定母单元中点A,(ξ,η),怎样求实际单元中与A,相对应的点A(x,y);反之,如果给定实际单元中的点A(x,y),怎样求其在母单元中对应点A,(ξ,η)?6、如果已经求解得到单元8个节点的位移值{δe}怎样求单元中某一点B(x,y)的应力?实际单元12435678AYX12435678η=1η=﹣1ηξ母单元ξ=1ξ=﹣1Aˊ1解:1、此题分两步进行:单元位移场的表达:如图1所示,在任意四边形的每边中间设一附加节点,则单元边界就变成二次曲线的了。如果直接在整体坐标系,xy下,像八节点矩形元那样,构造双二次多项式的位移插值函数,则因曲边四边形单元边界是二次曲线,故边界上的位移是()xy或的五次多项式,它不能由曲边上三个节点的位移分量唯一地决定,从而不能保证相邻两个单元在公共边上位移的协调条件,所以在整体坐标系,xy下构造完全协调的位移插值函数是很困难的,利用坐标变换,可将曲边四边形单元变换成基本单元,如图2所示的在自然坐标,下具有边长为2的八节点正方形单元,自然坐标系,是外节点坐标值为±1的局部坐标系。在自然坐标系的单元上构造协调的位移插值函数,其形状函数是较普通的,取位移分量为,的双二次多项式,即:2222123456782222910111213141516uaaaaaaaavaaaaaaaa(1-1)利用8个节点的16个位移分量可唯一确定16个待定常数1216,,aaa⋯,,若代入8个节点的局部坐标值,得:图1:在总坐标系中具有二次曲边的四边形单元图2:在自然坐标系中的曲边四边形的基本单元211523264536774881-1-1111-1-110-10010011-11-11-1-11101000011111111101001001-111-111-11-1010000uauaauuaauauauua(1-2)195102116123137141548161-1-1111-1-110-10010011-11-11-1-11101000011111111101001001-111-111-11-1010000vavavavavavaavva(1-3)将解出的16个待定常数1216,,aaa⋯,代入式(1-1)即得:811552266337744881811552266337744881iiiiiiuNuNuNuNuNuNuNuNuNuvNvNvNvNvNvNvNvNvNv(1-4a)也即:128eeuNNNvuIIIN(1-4b)其中I为二阶单元矩阵,e为等参元节点位移列阵,N为形状函数矩阵。形状函数的建立:按等参元思想,在整体坐标系XY下,任何形状歪斜四边形单元都将变换到局部坐标系下的正方形单元。对8节点等参元,其移模式为:81,iiiuNu(1-5)3式中,iu为歪斜单元8节点的位移,,iN为形状函数。查阅相关资料,得形函数公式公式为:8181,,,kkikiikFNF(1-6)又由形状函数的性质可具体地求出iN的表达式为:123425262728=1114=1114=1114=1114=112=112=112=112NNNNNNNN(1-7)2、根据平面问题的几何方程,单元应变可用节点位移表示如下:128=xeeyxy=BBBB(2-1)其中:0=0iiiiiNxNyNNyxB(2-2)即要求出矩阵iB中的元素iNx,iNy(1,2,,8)i。另根据符合函数求导法则,可知:4=iiiiiiNxyNNxxNNNxyyyJ(2-3)其中,J为二维坐标变化下的Jacobi矩阵,即:xyxyJ(2-4)其元素计算式为:81iiiNxx,81iiiNxx,81iiiNyy,81iiiNyy(2-5)又根据式(2-3),有1iiiiNNxNNyJ(2-6)根据公式(2-2)即可得出iB矩阵,其中iN可由问题1方法求出。3、单元刚度矩阵按普遍公式计算,公式如下:eeeTTkdVhdxdyBDBBDB(3-1)其中e为单元体积域,ek为16×16的方阵(具体形式见下文),D为材料的弹性系数矩阵,各向同性材料的弹性系数矩阵为:5101-1101121-1-2002-E(1)D(3-2)上述积分应在局部坐标系内进行,因此面积元素dxdy需表示成dd.如图3所示为子单元内任一点,axy处的微小正方形,它是由局部坐标系中点,处的微元体dd变换而成的。以,ij表示,xy轴的单位基矢量,,abac分别由,dd变换而成,则:xydab=ijxydac=ij(3-3)上述2个矢量的叉积表示它们所构成的平行四边形面积,故:dVJddabac(3-4)其中,J为矩阵J的行列式,即xyJxy将上式带入式(3-1),并写成分块...