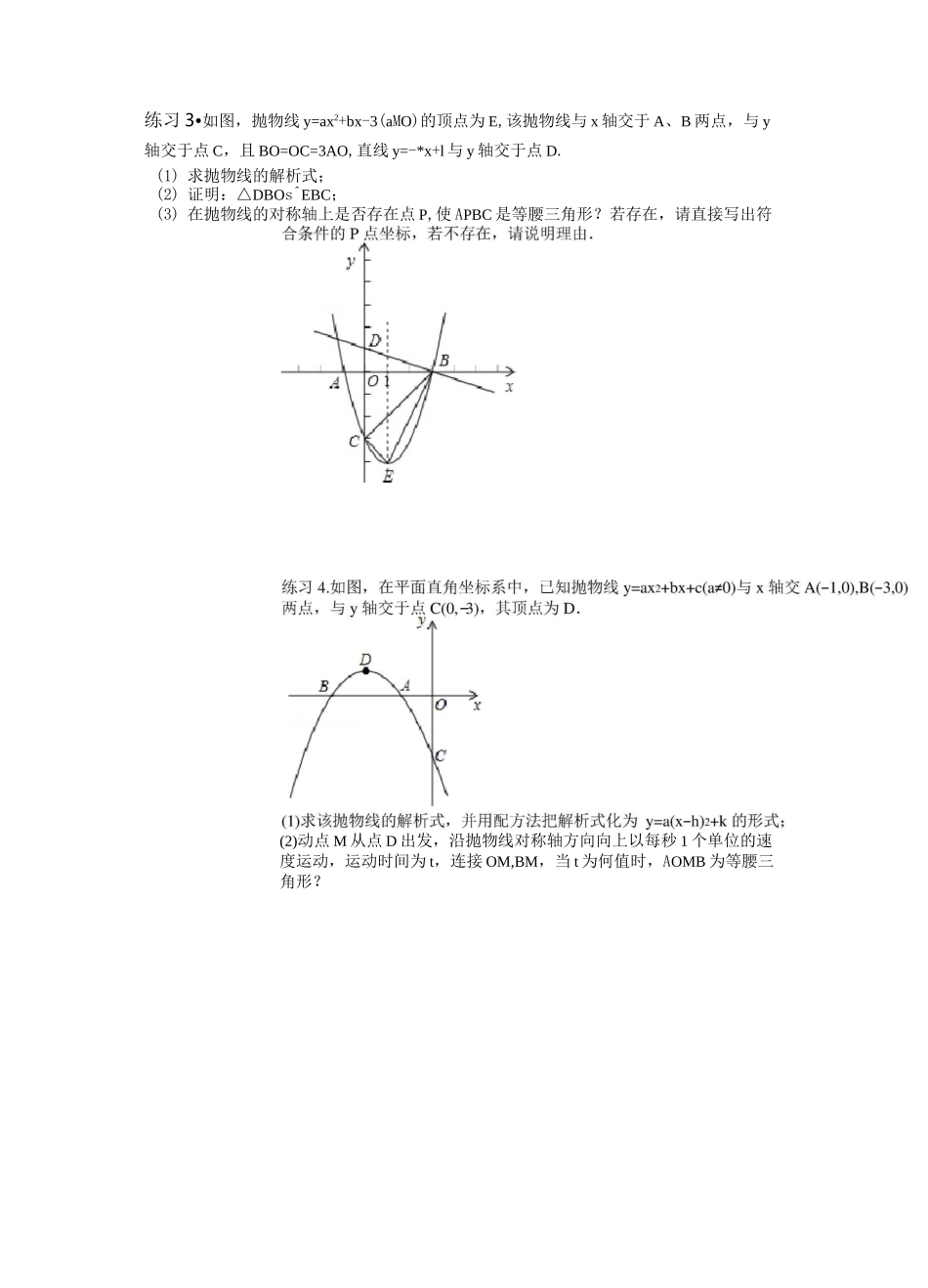
特殊图形存在性问题一、等腰三角形1、情景:平面内有点A、B,要找到点P使得AABP为等腰三角形。2、思想:分类讨论(1)A为顶点:AB=AP(以A为圆心、AB长为半径画圆)(2)B为顶点:AB=BP(以B为圆心、AB长为半径画圆)(3)P为顶点:PA=PB(AB中垂线)【注】:1.利用两圆一线,找到符合要求的点,如P在抛物线对称轴上,在x轴上等;然后将问题转化为,求线段等长。2.求线段等长:两点间距离(最笨的方法);向坐标轴做垂线,构造一线三等角例1•如图,抛物线y=-x2+2x+3y=-x2+2x+3与y轴交于点C,点D(O,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为.练习1.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直(1)求这个二次函数的表达式;⑵在直线BC找一点Q,使得△QOC为等腰三角形,写出Q点坐标.练习2、已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线1是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线1上的一个动点,当APAC的周长最小时,求点P的坐标;(3)在直线1上是否存在点M,使AMAC为等腰三角形?若存在,直接写出所有符合条件练习3•如图,抛物线y=ax2+bx-3(aMO)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=-*x+l与y轴交于点D.(1)求抛物线的解析式;(2)证明:△DBOs^EBC;(3)在抛物线的对称轴上是否存在点P,使APBC是等腰三角形?若存在,请直接写出符(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,AOMB为等腰三角形?练习5•如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,-n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(mVn)分别是方程x2-2x-3=0的两根.(1)求抛物线的解析式;(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.25.(10分)如图,在平面直角坐标系中,抛物线y=*x2+bx+c经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).(I)求抛物线的解析式及它的对称轴;(II)点P(0,n)在线段OB上,点Q在线段BC上,若OP=2BQ,且PA=QA.求n的值;(III)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角19-红桥一模25.(10分)如图,抛物线y=x2+bx+c与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0).(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE〃AC,交BC于E,连接CP,求MCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且AOMD为等腰三角形,求M点的坐标.(17河北一模)25(10分)如图,己知抛物线y=x2+bx+c图象经过点A(-1,0),B(0,-3),抛物线与x轴的另一个交点为C.(1)求这个抛物线的解析式:(2)若抛物线的对称轴上有一动点D,且“BCD为等腰三角形(CB*CD\,试求点D的坐标;二、直角三角形1.情景:平面内有点A、B,要找到点P使得△ABP为直角三角形2.思想:分类讨论(1)A为顶点:ZA(过A做垂线)(2)B为顶点:ZB(过B做垂线)(3)P为顶点:ZC(AB为直径的圆)【注】1.等腰直角三角形,只需在两直线上上下找与AB等长以及过O做AB垂线与圆交点即可(2)在抛物线上是否存在点Q,使AQBF为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.练习1•如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tanZABO=13(1)求抛物线的对称轴和PP的坐标.(2)在抛物线的对称轴上是否存在这样的点D,使△ABD为直角三角形?如果存在,求点D的坐标;如果不存在,请说明理由.例2.如图,抛物线y=-x2+bx+c与x轴相交于AB两点,与y轴相交与点C,且点B与点CC的坐标分别为(3,0),C(0,3),点M是抛物线的顶点.(1)求二次函数的关系式⑵在MB上是否存在点P,过点P作PD丄x轴于点D,OD=m,使△PCD为直角三角形?如练习3•如图,抛物线y=x2+bx+c与直线y詰"X-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC丄x轴...