课件三角函数VIP免费

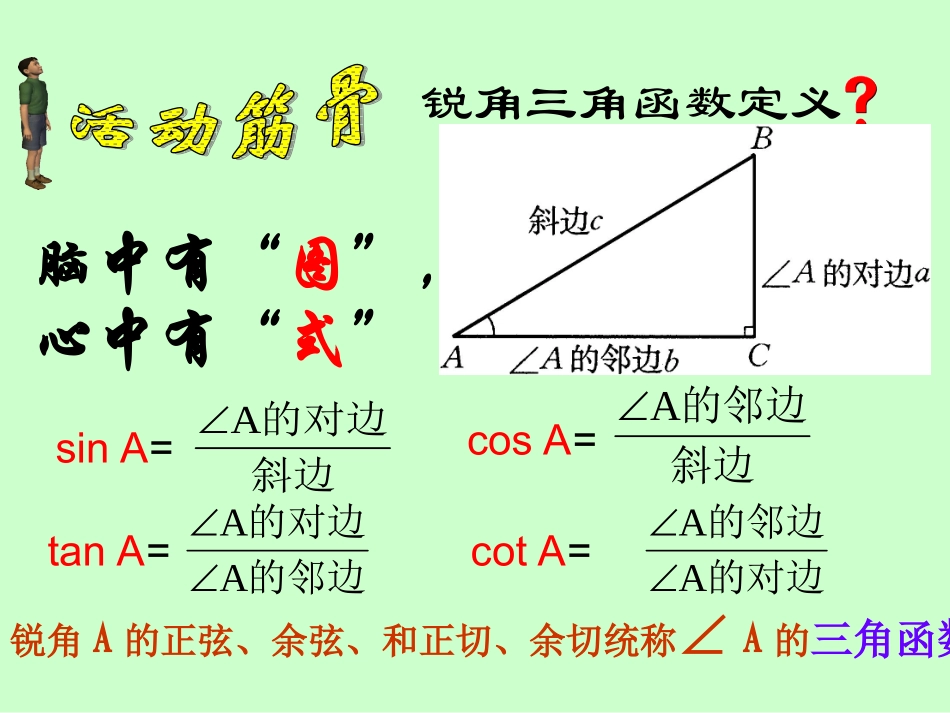
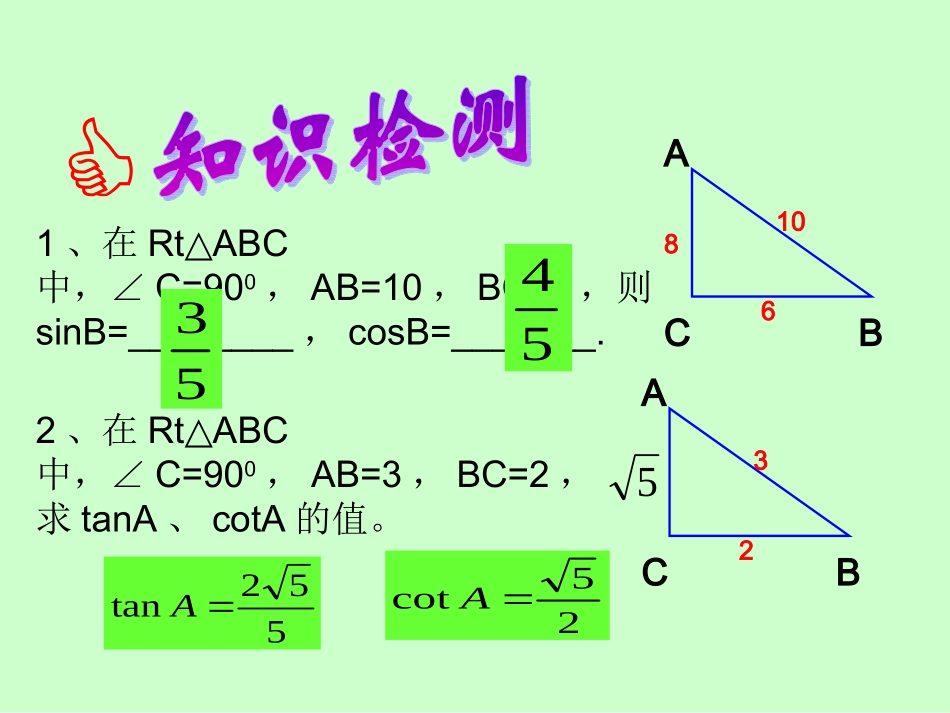
锐角三角函数定义锐角A的正弦、余弦、和正切、余切统称∠A的三角函数sinA=斜边的对边AcosA=斜边的邻边AtanA=的邻边的对边AAcotA=的对边的邻边AA图19.3.1脑中有“图”，心中有“式”1、在RtABC△中，∠C=900，AB=10，BC=6，则sinB=________，cosB=_______.ABC1062、在RtABC△中，∠C=900，AB=3，BC=2，求tanA、cotA的值。ABC32545825cotA552tanA53300,450,600角的三角函数值如图,观察一副三角板:它们其中有几个锐角?分别是多少度?(1)sin300等于多少?┌┌300600450450(2)cos300等于多少?(3)tan300等于多少?(4)cot300等于多少?ABC30°123sin30°=cos30°=tan30°=cot30°=2123333300角的各类三角函数值的探索在直角三角形中，如果一个锐角等于300，那么它所对的直角边等于斜边的一半。(5)sin450,sin600等于多少?(6)cos450,cos600等于多少?(7)tan450,tan600等于多少?(8)cot450,cot600等于多少?┌┌300600450450请同桌之间展开讨论三角函数锐角α正弦sinα余弦cosα正切tanα3004506002123332222123213余切cotα3133例1：计算:(1)sin300+cos450;(2)sin2600+cos2600-tan450.老师提示:Sin2600表示(sin600)2,cos2600表示(cos600)2,其余类推.计算:1、3tan30°+2cot45°+2sin60°2、角为锐1sin1sin2.45cos260sin45sin221000.45cos260cos30sin222020202请在三分钟内完成以下两小题根据条件求锐角：1：已知tanA·cot20°=1求∠A。2：已知：求∠A，∠B的度数。3：已知3cot(A－10°)=求∠A4：已知2cosA－1=0,求∠A,03sin23tan2AB32独立作业.如图,身高1.5m的小丽用一个两锐角分别是300和600的三角尺测量一棵树的高度.已知她与树之间的距离为5m,那么这棵树大约有多高?例题赏析例3如图，在△ABC中，AD是BC边上的高，若tanB=cos∠DAC，（１）AC与BD相等吗？说明理由；（２）若sinC＝，BC=１２，求AD的长。１２１３DCBA解cos∠DAC在Rt△ABD和△ACD中，tanB=，＝ADBDADAC因为tanB=cos∠DAC，所以＝ADBDADAC故BD=AC（１）例题赏析DCBA如图，在△ABC中，AD是BC边上的高，若tanB=cos∠DAC，（１）AC与BD相等吗？说明理由；（２）若sinC＝，BC=１２，求AD的长。１２１３解（２）设AC=13k,AD=12k，所以CD=5k,又AC=BD=13k，所以BC=18k=12,故k=２３在Rt△ACD中，因为sinC＝１２１３所以AD=12×＝８２３1、300,450,600角的三角函数值2、三角函数值的计算与应用当堂训练一1，在Rt△ABC中，如果各边都扩大2倍，则锐角A的正弦值和余弦值（）A，都不变B，都扩大2倍C，都缩小2倍D，不确定。√22sinA=,tanB=√3，则∠C=2，在△ABC中，若3,在Rt△ABC中,∠C=90°,AC=√3,AB=2,tanB24，如果α和β都是锐角，且sinα=cosβ，则α与β的关系是（）A，相等B，互余C，互补D，不确定。5，已知在Rt△ABC中,∠C=90°，sinA=,则cosB=()12√32√2221√3AB，C，D，A75°√33BA3,在Rt△ABC中,∠C=90°,AC=√3,AB=2,tanB24，如果α和β都是锐角，且sinα=cosβ，则α与β的关系是（）A，相等B，互余C，互补D，不确定。例题赏析（1）计算：sin60°·tan60°+cos²45°=（2）如果tanA·tan30°=1,∠A=_________。（3）已知cosα<0.5,那么锐角α的取值范围（）A、60°<α<90°B、0°<α<60°C、30°<α<90°D、0°<α<30°（4）如果√cosA–—+|√3tanB–3|=012那么△ABC是（）A、直角三角形B、锐角三角形C、钝角三角形D、等边三角形。260°AD²当堂训练二