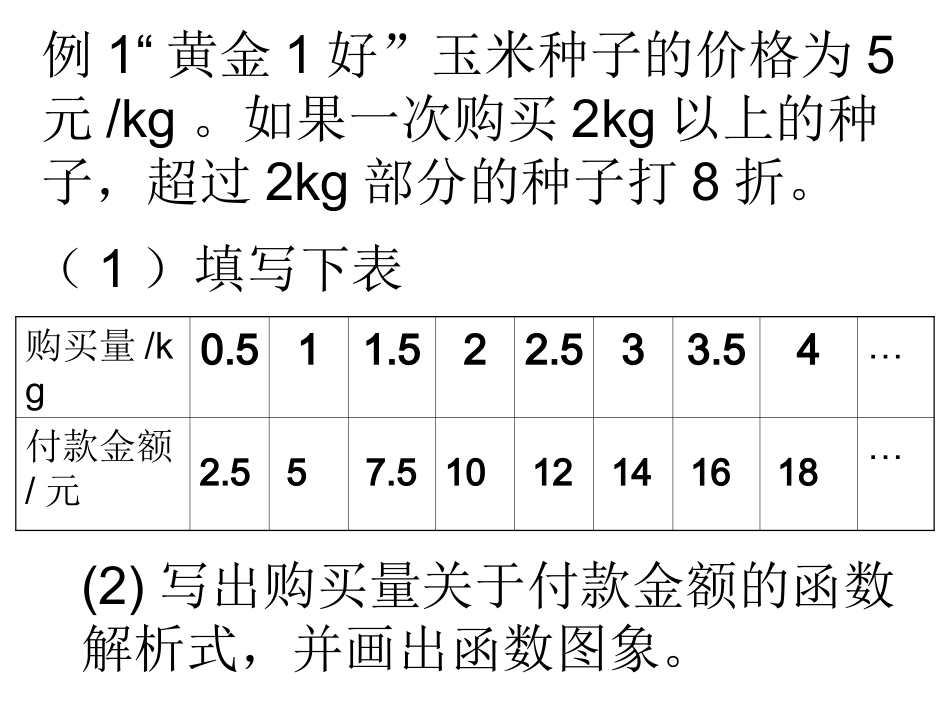
第十九章一次函数第五课时,一次函数的应用我们前面学习了有关一次函数的一些知识及如何确定解析式,如何利用一次函数知识解决相关实践问题呢?这将是我们这节课要解决的主要问题.提出问题,创设情境新课探究例1“黄金1好”玉米种子的价格为5元/kg。如果一次购买2kg以上的种子,超过2kg部分的种子打8折。(1)填写下表购买量/kg0.511.522.533.54…付款金额/元…2.557.51012141618(2)写出购买量关于付款金额的函数解析式,并画出函数图象。分析:付款金额与种子价格相关,问题中种子价格不是固定不变的,它与购买量有关。设购买xkg种子,当0≤x≤2时,种子价格为5元/kg;当x>2时,其中有2kg种子按5元/kg计价,其余的(x-2)kg(即超出2kg部分)种子按4元/kg(即8折)计价。因此,写函数解析式与画函数图象时,应对0≤x≤2和x>2分段讨论。我们把这种函数叫做分段函数.在解决分析函数问题时,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.yx03510(1)填表:如上表。(2)设购买xkg种子,付款金额为y元。当0≤x≤2时,函数解析式为:y=5x当x>2时,函数解析式为:y=4(x-2)+10=4x+2,即y=4x+2函数图象如右图:y=5xy=4x+2解:例3今年入夏以来,全国大部分地区发生严重干旱.某市自来水公司为了鼓励市民节约用水,采取分段收费标准,若某户居民每月应交水费y(元)是用水量x(吨)的函数,当0≤x≤5时,y=0.72x,当x>5时,y=0.9x-0.9.(1)画出函数的图象;(2)观察图象,利用函数解析式,回答自来水公司采取的收费标准.分析:画函数图象时,应就自变量0≤x≤5和x>5分别画出图象,当0≤x≤5时,是正比例函数,当x>5是一次函数,所以这个函数的图象是一条折线.解:(1)函数的图象是:(2)自来水公司的收费标准是:当用水量在5吨以内时,每吨0.72元;当用水量在5吨以上时,每吨0.90元.课堂练习1、小芳以200米/分的速度起跑后,先匀加速跑5分钟,每分提高速度20米/分,又匀速跑10分钟.试写出这段时间里她跑步速度y(米/分)随跑步时间x(分)变化的函数关系式,并画出图象.分析:本题y随x变化的规律分成两段:前5分钟与后10分钟.写y随x变化函数关系式时要分成两部分.画图象时也要分成两段来画,且要注意各自变量的取值范围.解:y=)<()<15530050(20020xxxx2、教材P95,练习,第2题。课堂小结本节课我们学习并掌握了分段函数在实际问题中的应用,特别是学习了解决多个变量的函数问题,为我们以后解决实际问题开辟了一条坦途,使我们进一步认识到学习函数的重要性和必要性.教材P99,习题19.29、10、12题课后作业