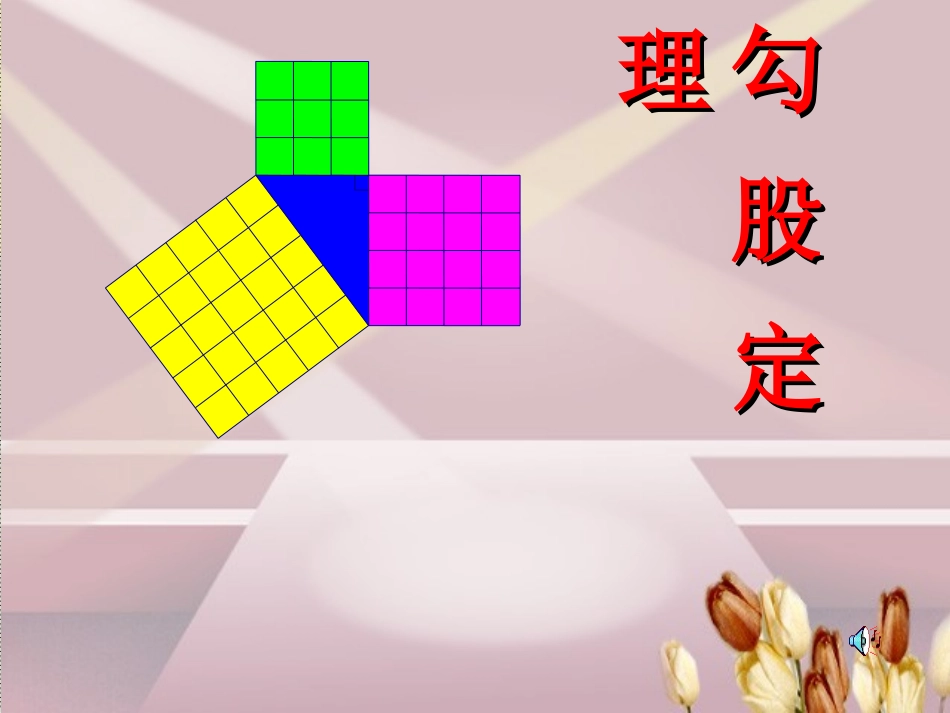
勾股定勾股定理理邮票赏邮票赏析析这是1955年希腊曾经发行的纪念一位数学家的邮票。这就是本届大会会徽的图案.活动1你见过这个图案吗?你听说过勾股定理吗?这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.活动2相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.我们也来观察右图中的地面,看看有什么发现?1.观察图1-1(图中每个小方格代表一个单位面积)ABC图1-1正方形A中含有个小方格,即A的面积是个单位面积.正方形B的面积是个单位面积.正方形C的面积是个单位面积.9918你是怎样得到上面的结果的?与同伴交流交流.1239继续•••••••••••••••••••••••••正方形周边上的格点数a=12正方形内部的格点数b=13利用皮克公式112Sab所以,正方形C的面积为:112131182返回CAB图1-1图1-1CS正方形1433182分割成若干个直角边为整数的三角形返回CABCS正方形216218把C看成边长为6的正方形面积的一半CAB图1-1返回ABC图1-2ABC图1-32.观察右边两个图并填写下表:A的面积B的面积C的面积图1-2图1-3169254913你是怎样得到表中的结果的?与同伴交流交流.做一做ABC图1-2ABC图1-33.三个正方形A,B,C面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.议一议ABC图1-2ABC图1-34.你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流.5.分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.第4题中的关系对这个三角形仍然成立吗?222abc直角三角形两直角边的平方和等于斜边的平方.abc是不是所有的直角三角形都具有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.下面我们就来看一看我国数学家赵爽是怎样证明这个命题的.结论cba(b-a)2中黄实朱实活动3看左边的图案,这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形(黄色).赵爽弦图的证法224()42SSSabcba大正方形小正方形直角三角形化简得:c2=a2+b2.cba(b-a)2中黄实朱实勾股定理如果直角三角形两直角边分别为a、b,斜边为c,那么222abc直角三角形两直角边的平方和等于斜边的平方.abc1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③625576144169比一比看看谁算得快!2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x1、如图,一个高3米,宽4米的大门,需在相对角的顶点间加一个加固木条,则木条的长为()A.3米B.4米C.5米D.6米C342、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为()ABCA.50米B.120米C.100米D.130米130120?A一个门框的尺寸如图,一块长3米,宽2.2米的薄木板能否从门框内通过?为什么?•如图,一个3米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5米,如果梯子的顶端A沿墙下滑0.5米,那么梯子低端B也外移0.5米吗?3、在波平如静的湖面上,有一朵美丽的红莲,它高出水面1米,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为2米,问这里水深多少?x+1BCAH12?┓xx2+22=(x+1)2盛开的水莲盛开的水莲小结:小结:活动活动44布置作业:布置作业:勾股定理从边的角度刻画了直角三角形勾股定理从边的角度刻画了直角三角形的又一个特征.的又一个特征.人类对勾股定理的研究已有近人类对勾股定理的研究已有近30003000年的年的历史,在西方,勾股定理又被称为“毕达哥拉斯历史,在西方,勾股定理又被称为“毕达哥拉斯定理”、“百牛定理”、“驴桥定理”等等.定理”、“百牛定理”、“驴桥定理”等等.