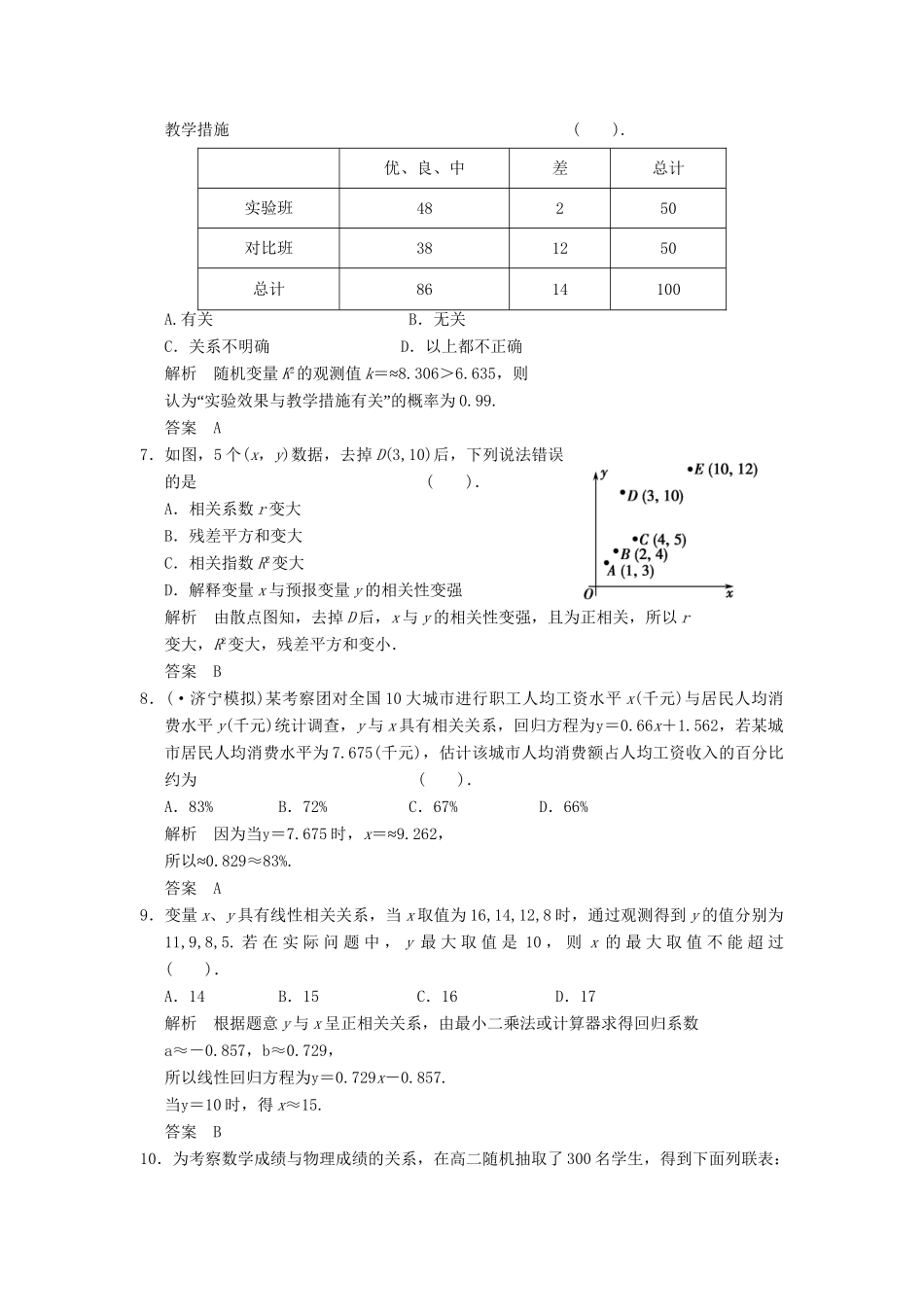
章末质量评估(三)(时间:100分钟满分:120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列有关线性回归的说法不正确的是().A.变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系B.在平面直角坐标系中用描点的方法得到具有相关关系的两个变量的一组数据的图形叫做散点图C.线性回归直线得到具有代表意义的回归直线方程D.任何一组观测值都能得到具有代表意义的回归直线方程解析任何一组观测值并不能都得到具有代表意义的回归直线方程.答案D2.身高与体重有关系可以用________分析来分析().A.残差B.回归C.等高条形图D.独立检验解析因为身高与体重是两个具有相关关系的变量,所以要用回归分析来解决.答案B3.设有一个回归方程为y=3-5x,当变量x增加一个单位时().A.y平均增加3个单位B.y平均减少5个单位C.y平均增加5个单位D.y平均减少3个单位解析-5是斜率的估计值,说明x每增加一个单位,y平均减少5个单位.答案B4.已知一个线性回归方程为y=1.5x+45,其中x的取值依次为1,7,5,13,19,则y=().A.58.5B.46.5C.60D.75解析x==9,因为回归直线方程过点(x,y),所以y=1.5×x+45=1.5×9+45=58.5.答案A5.一位母亲记录了儿子3~9岁的身高,数据略,由此建立的身高与年龄的回归模型为y=7.19x+73.93,用这个模型预测这个孩子10岁时的身高,则正确的叙述是().A.身高一定是145.83cmB.身高在145.83cm以上C.身高在145.83cm左右D.身高在145.83cm以下解析回归模型只能进行预测,应选C.答案C6.在两个学习基础相当的班级实行某种教学措施的实验,测试结果见下表,则实验效果与教学措施().优、良、中差总计实验班48250对比班381250总计8614100A.有关B.无关C.关系不明确D.以上都不正确解析随机变量K2的观测值k≈=8.306>6.635,则“”认为实验效果与教学措施有关的概率为0.99.答案A7.如图,5个(x,y)数据,去掉D(3,10)后,下列说法错误的是().A.相关系数r变大B.残差平方和变大C.相关指数R2变大D.解释变量x与预报变量y的相关性变强解析由散点图知,去掉D后,x与y的相关性变强,且为正相关,所以r变大,R2变大,残差平方和变小.答案B8.(·济宁模拟)某考察团对全国10大城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查,y与x具有相关关系,回归方程为y=0.66x+1.562,若某城市居民人均消费水平为7.675(千元),估计该城市人均消费额占人均工资收入的百分比约为().A.83%B.72%C.67%D.66%解析因为当y=7.675时,x≈=9.262,≈所以0.829≈83%.答案A9.变量x、y具有线性相关关系,当x取值为16,14,12,8时,通过观测得到y的值分别为11,9,8,5.若在实际问题中,y最大取值是10,则x的最大取值不能超过().A.14B.15C.16D.17解析根据题意y与x呈正相关关系,由最小二乘法或计算器求得回归系数a≈-0.857,b≈0.729,所以线性回归方程为y=0.729x-0.857.当y=10时,得x≈15.答案B10.为考察数学成绩与物理成绩的关系,在高二随机抽取了300名学生,得到下面列联表:数学物理85~100分85分以下总计85~100分378512285分以下35143178总计72228300现判断数学成绩与物理成绩有关系,则判断的出错率为().A.0.5%B.1%C.2%D.5%解析代入公式得K2的观测值k≈=4.514>3.841,查表可得.答案D二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)11.从某地区15000位老人中随机抽取500人,其生活能否自理的情况如下表所示:男女能178278不能2321则该地区生活不能自理的老人中男性比女性约多________人.解析由表中数据可知,男性不能自理的频率为,女性不能自理的频率为,故15000×=60(人).答案6012.(·湖南六校联考)甲、乙、丙、丁四位同学各自对A,B两个变量的线性相关性做试验,并用回归分析方法分别求得相关系数r与残差平方和m如下表:甲乙丙丁r0.820.780.690.85m106115124103则这四位同学中,________同学的试验结果体现A,B两个变量有更强的线性相关性.解析由题中表可知,丁同学的相关系数最大且残差平方和最小,故丁同学的...