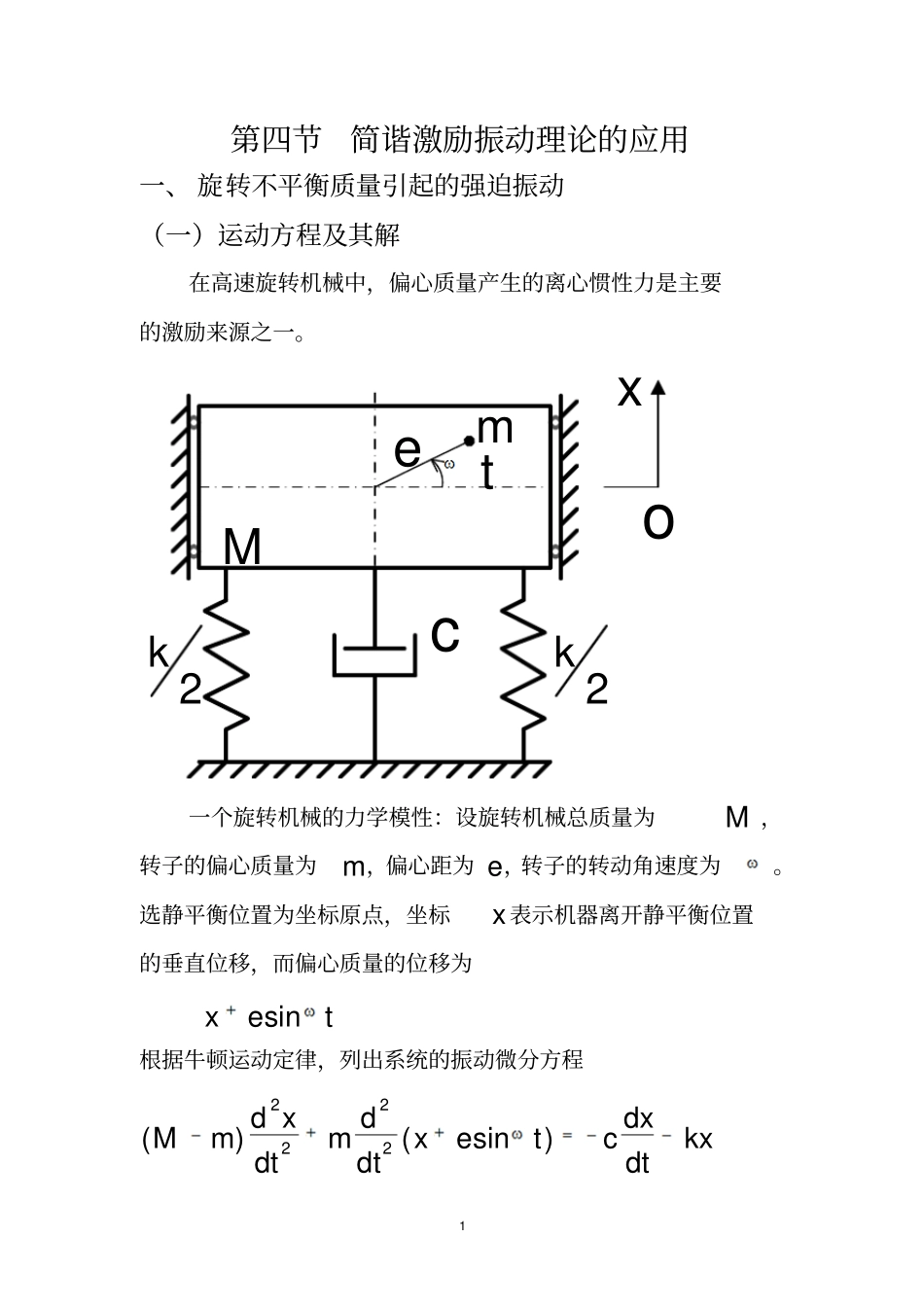
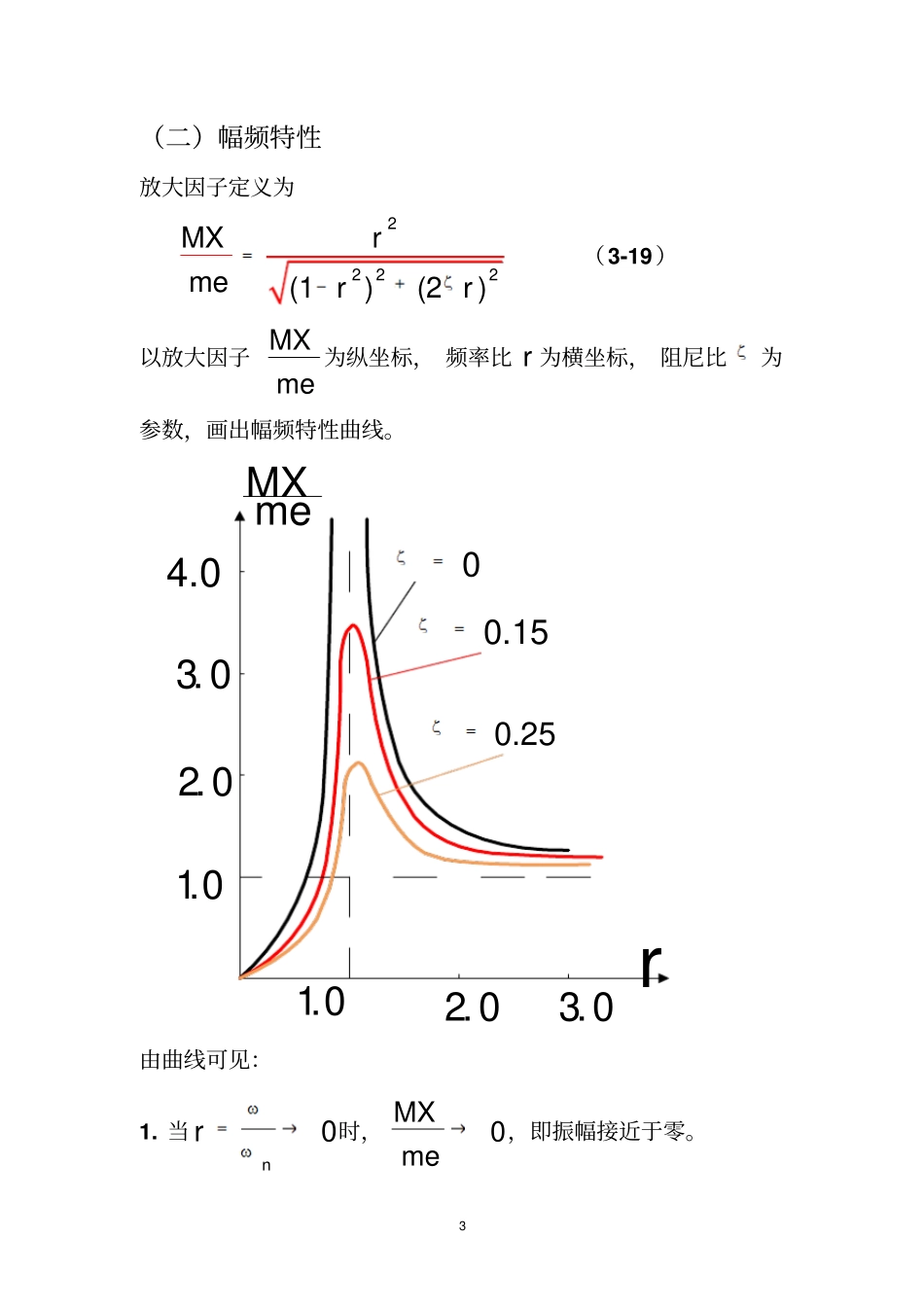
1第四节简谐激励振动理论的应用一、旋转不平衡质量引起的强迫振动(一)运动方程及其解在高速旋转机械中,偏心质量产生的离心惯性力是主要的激励来源之一。Memt2k2kcxo一个旋转机械的力学模性:设旋转机械总质量为M,转子的偏心质量为m,偏心距为e,转子的转动角速度为。选静平衡位置为坐标原点,坐标x表示机器离开静平衡位置的垂直位移,而偏心质量的位移为sinxet根据牛顿运动定律,列出系统的振动微分方程2222()(sin)dxddxMmmxetckxdtdtdt2整理后,得2sinMxcxkxmet(3-18)上式的形式与方程(3-1)相似,只是由2me代替了0F,故前面所有的分析都可适用。设nkM,2ncM,nr则方程(3-18)的稳态响应为()sin()xtXt式中振幅X为222222222222()()1(1)(2)(1)(2)meXkMcmekrrmerMrr显然,相位差为2221crtgkmr可见,偏心质量引起的强迫振动的振幅与不平衡质量me成正比。为了减小振动,旋转机械的转子通常要作平衡试验,使质量分布尽可能均匀。3(二)幅频特性放大因子定义为2222(1)(2)MXrmerr(3-19)以放大因子MXme为纵坐标,频率比r为横坐标,阻尼比为参数,画出幅频特性曲线。1.02.03.04.01.02.03.0MXmer00.150.25由曲线可见:1.当0nr时,0MXme,即振幅接近于零。42.当1nr时,1MXme,即振幅趋近于常数,即meXM而与激励频率及阻尼比基本上无关。3.共振发生在2112r即212n时,位于1r的右边,共振振幅为2121meXM当阻尼很小时(0.2),可以认为当1r即n发生共振,共振振幅为2memeXMc5例题:一台惯性式激振器安放在机器正上方,以测定机器的振动特性。激振器有一对带有偏心质量、等速反向旋转的齿轮组成。当旋转角速度ω为时,偏心质量的离心惯性力在水平方向合力为零,在垂直方向合成激振力meω2sinωt,其中m为总的偏心质量,e为偏心距。通过改变转速,测得共振时的垂直振幅为1.07cm,而超过共振很远时,垂直振幅趋于定值0.32cm。若偏心质量为12.7kg,偏心距为15cm,支承弹簧刚度为k=976.7N/cm。计算(1)支承阻尼器的阻尼比;(2)转速为N=300r/min时机器的垂直振幅。..Mk/2k/2c6解:设机器和激振器的总质量为M。系统的振动微分方程为2sinMxcxkxmet(1)共振时(r=1)的振幅为max1.072meXcmM而r>>1(超过共振很远时)时有0.32meXcmM所以阻尼比max0.320.15221.07XX(2)当转速为N=300r/min时,激励频率为2230031.46060N(rad/s)由nkM和meXM,得97.61000.3212.812.715nkXme(rad/s)频率比31.42.4512.8nr则机器的振幅为22222222.450.320.38()(12.45)(20.(1152.45))(2)merXMrmrc7例3-2:桥式起重机运行机构采用高速空心轴传动,轴的两端由调位轴承支承,轴上无别的零件。空心轴的内径d1为,外径为d2,两支承间距离为l,求轴的临界转速(r/min)。lEI,2m轴的临界转速ncr为:602ncrn。故只要知道梁的固有频率即可求出轴的临界转速ncr。求连续梁第一阶固有频率时,其模型可按如下简化(离散化):将梁离散为三点:两个端点和一个中点,其中梁的两端端点的质量各为总质量的四分之一,即242mm,中点的质量为总质量的二分之一,即22mm。如图所示。这样处理后,可以把梁看作是抗弯刚度为EI、无质量的弹性梁。lEI·/2l/2m··m/2m/2由静变形法,知348ngEIml8式中Δ是梁中点的静变形,由材力知348mglEI9二、基础运动引起的强迫振动在许多情况下,系统受到的激励来自于支承的运动,例如固定在机器上的仪表,汽车在不平的路面行驶时的振动等等,都是支承运动引起的强迫振动。(一)运动方程及其解ckmxyYtm()kxy()cxy如图所示是受基础激励的振动力学模型。以系统静平衡位置为坐标原点建立坐标系:x----质量块的位移y----基础的位移设基础运动规律为sinyYt由牛顿运动定律,得()()mxkxycxy(3-20)即mxcxkxkycy(a)或也可写成:sincosmxcxkxkYtcYt10利用复指数法求解上式。用jtyYe代换sinyYt,所以jtyjYe,代入式(a),得()jtjtjtmxcxkxkYejcYekjcYe(b)假定方程(b)的解为()jtxtXe(c)式中X----复振幅则()jtxtjXe2()jtxtXe带入方程(b),得2[()]()jtjtkmjcXekjcYe∴2()jtkjcXYXekmjc(d)则实振幅为222222222()()()1(2)(1)(2)kcXXYkmcrYrr(e)相位差11322322()()21(2)mctgkkmcrrr(3-27)故方程(b)...