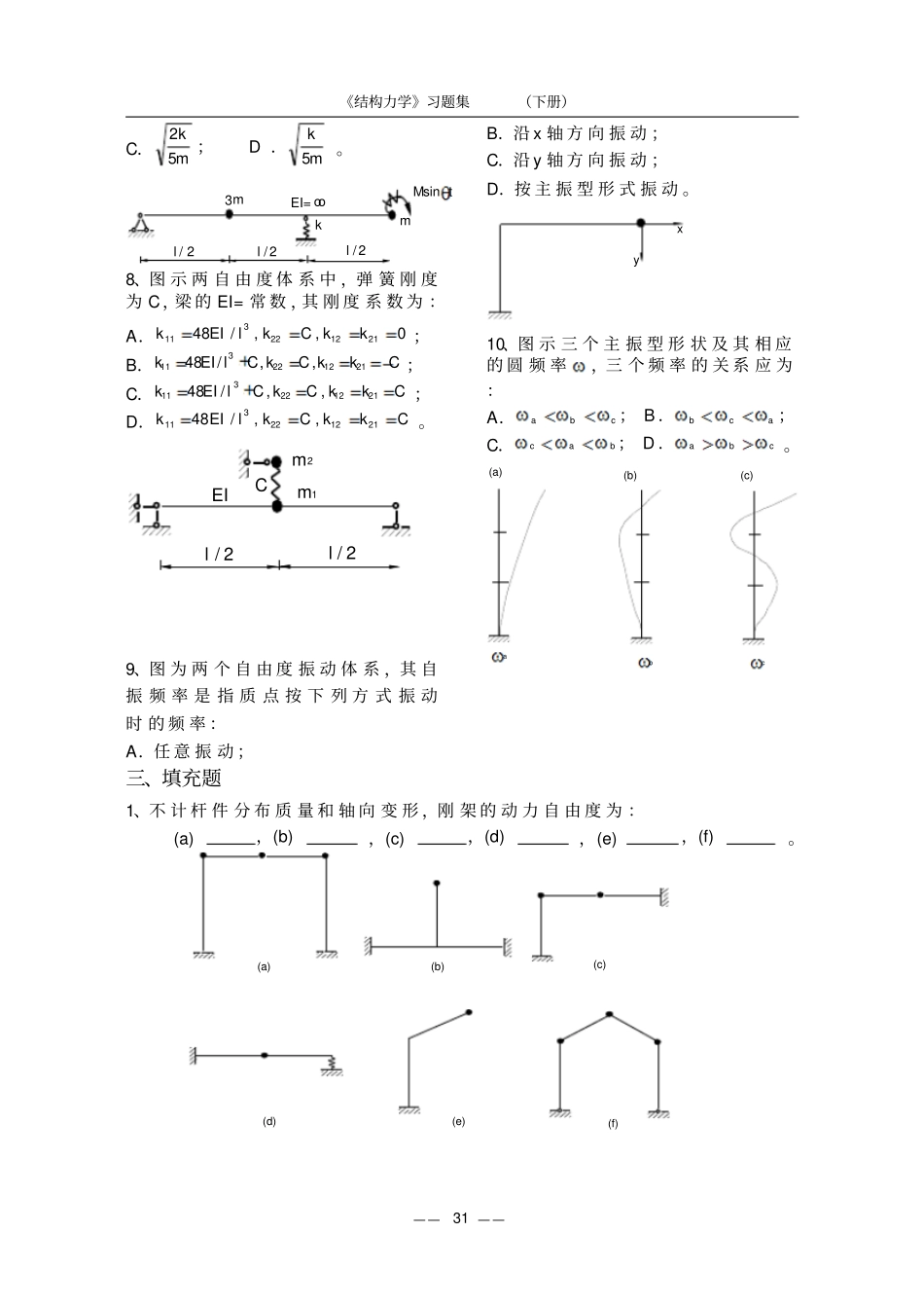
《结构力学》习题集(下册)————28第九章结构动力计算一、是非题1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。2、忽略直杆的轴向变形,图示结构的动力自由度为4个。3、仅在恢复力作用下的振动称为自由振动。4、单自由度体系其它参数不变,只有刚度EI增大到原来的2倍,则周期比原来的周期减小1/2。5、图a体系的自振频率比图b的小。ml/2l/2EIml/2l/2EI(a)(b)6、单自由度体系如图,W98.kN,欲使顶端产生水平位移001.m,需加水平力P16kN,则体系的自振频率40s1。WP7、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。8、由于阻尼的存在,任何振动都不会长期继续下去。9、桁架ABC在C结点处有重物W,杆重不计,EA为常数,在C点的竖向初位移干扰下,W将作竖向自由振动。ABWC10、不计阻尼时,图示体系的运动方程为:mmXXhEIEIEIEIXXPt00148242424012312()二、选择题1、图示体系,质点的运动方程为:oolEIEImEI0mEIEIooEI0P()t12《结构力学》习题集(下册)————30A.ylPsinmyEI77683t/;B.myEIylPsin/19273t;C.myEIylPsin/38473t;D.ylPsinmyEI7963t/。llm0.50.5EIPtsin()2、在图示结构中,若要使其自振频率增大,可以A.增大P;B.增大m;C.增大EI;D.增大l。lEImPtsin()3、单自由度体系自由振动的振幅取决于:A.初位移;B.初速度;C.初位移、初速度与质量;D.初位移、初速度与结构自振频率。4、考虑阻尼比不考虑阻尼时结构的自振频率:A.大;B.小;C.相同;D.不定,取决于阻尼性质。5、已知一单自由度体系的阻尼比12.,则该体系自由振动时的位移时程曲线的形状可能为:ytD.C.B.A.ytytyt6、图a所示梁,梁重不计,其自振频率76873EIml/;今在集中质量处添加弹性支承,如图b所示,则该体系的自振频率为:A.76873EImlkm//;B.76873EImlkm//;C.76873EImlkm//;D.76873EImlkm//。llmEI/2/2llmEI/2/2k(a)(b)7、图示结构,不计阻尼与杆件质量,若要其发生共振,应等于A.23km;B.km3;《结构力学》习题集(下册)————31C.25km;D.km5。Mtsinmool/2EI=l/2l/2m3k8、图示两自由度体系中,弹簧刚度为C,梁的EI=常数,其刚度系数为:A.kEIlkCkk113221221480/,,;B.kEIlCkCkkC11322122148/,,;C.kEIlCkCkkC11322122148/,,;D.kEIlkCkkC11322122148/,,。l/2l/2EIm1C2m9、图为两个自由度振动体系,其自振频率是指质点按下列方式振动时的频率:A.任意振动;B.沿x轴方向振动;C.沿y轴方向振动;D.按主振型形式振动。xy10、图示三个主振型形状及其相应的圆频率,三个频率的关系应为:A.abc;B.bca;C.cab;D.abc。(a)(b)(c)abc三、填充题1、不计杆件分布质量和轴向变形,刚架的动力自由度为:(a),(b),(c),(d),(e),(f)。(a)(b)(c)(e)(f)(d)《结构力学》习题集(下册)————492、图示组合结构,不计杆件的质量,其动力自由度为个。3、图示简支梁的EI=常数,其无阻尼受迫振动的位移方程为。m/3l/3l/3lPtsin4、图示体系的自振频率。llEImlEAEAmEI=1oo5、图示体系中,已知横梁B端侧移刚度为k1,弹簧刚度为k2,则竖向振动频率为。mk1k2BA6、在图示体系中,横梁的质量为m,其EI1;柱高为l,两柱EI=常数,柱重不计。不考虑阻尼时,动力荷载的频率时将发生共振。Psint7、单自由度无阻尼体系受简谐荷载作用,若稳态受迫振动可表为yytstsin,则式中计算公式为,yst是。8、图示体系不计阻尼,2(为自振频率),其动力系数。Ptsin()9、图示体系竖向自振的方程为:yIIyII11111222211222,,其中22等于。m1212mkky10、多自由度体系自由振动时的任何位移曲线,均可看成的线性组合。四、计算题《结构力学》习题集(下册)————321、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k,求自振频率。EIWool/2l/2k2、求图示体系的自振频率。mlEIEIl0.5l0.523、求图示体系的自振频率。EI=常数。mll0.54、求图示结构的自振频率。mllllEI=常数5、求图示体系的自振频率。EI常数,杆长均为l。m6、求图示体系的自振频率。杆长均为l。EA=ooEImEIEI7、图示梁自重不计,WEI2002104kNkNm2,,求自振圆频率。EIWABC2m2m8、求图示单自由度体系的自振...