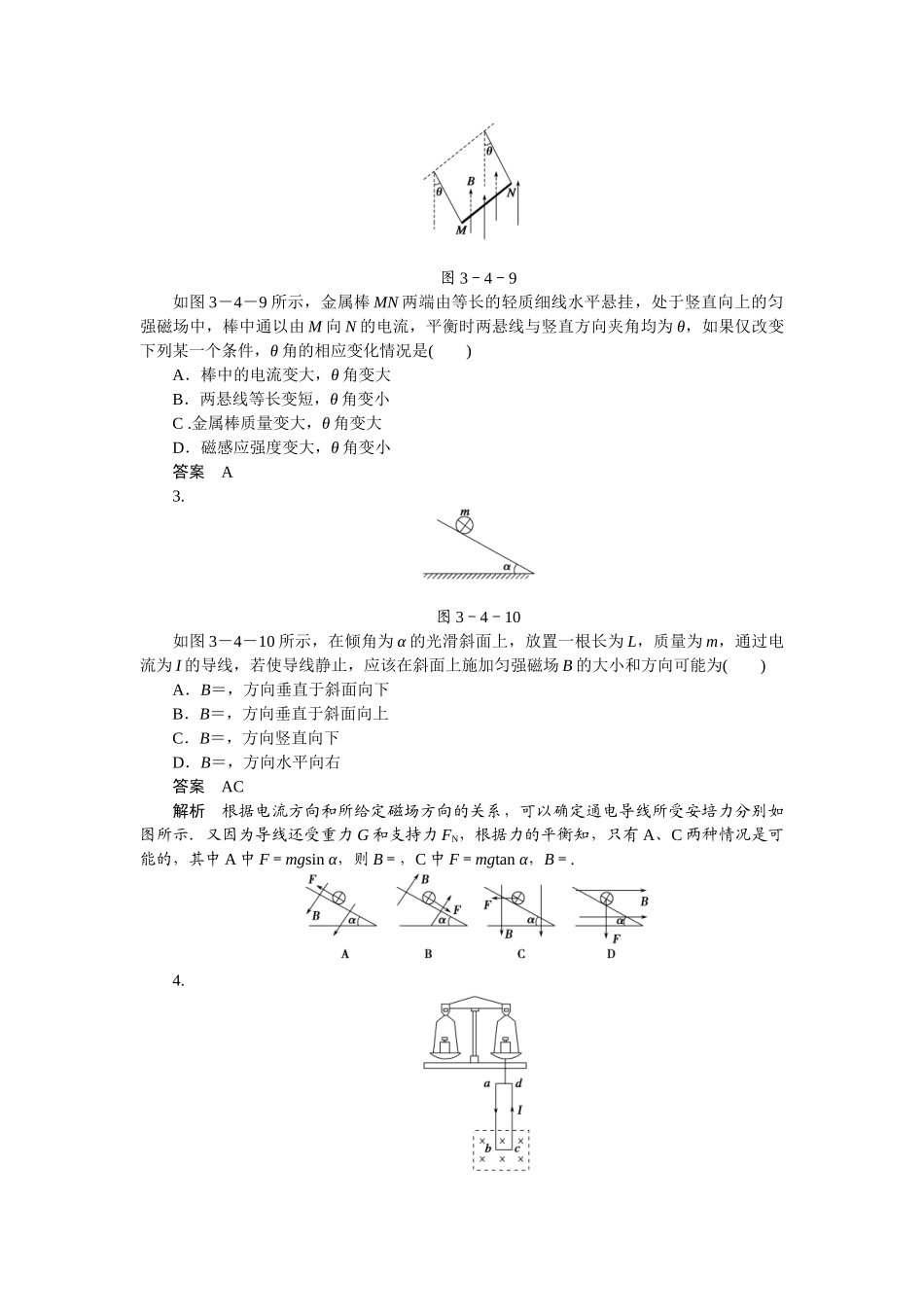
安培力作用下导体的平衡1.图3-4-5如图3-4-5所示,用两根轻细金属丝将质量为m、长为l的金属棒ab悬挂在c、d两处,置于匀强磁场内.当棒中通以从a到b的电流I后,两悬线偏离竖直方向θ角而处于平衡状态.为了使棒平衡在该位置上,所需的磁场的最小磁感应强度的大小、方向为()A.tanθ,竖直向上B.tanθ,竖直向下C.sinθ,平行悬线向下D.sinθ,平行悬线向上答案D解析要求所加磁场的磁感应强度最小,应使棒平衡时所受的安培力有最小值.由于棒的重力恒定,悬线拉力的方向不变,如图所示,由画出的力的三角形可知,安培力的最小值为Fmin=mgsinθ,即IlBmin=mgsinθ,得Bmin=sinθ,方向应平行于悬线向上.故选D.2.图3-4-6如图3-4-6所示,在倾角为θ的斜面上,有一质量为m的通电长直导线,电流方向如图,当导线处于垂直于斜面向上的匀强磁场中,磁感应强度大小分别为B1和B2时,斜面对长直导线的静摩擦力均达到最大值,已知B1∶B2=3∶1,求斜面对长直导线的最大静摩擦力的大小.答案mgsinθ解析假设最大静摩擦力为fm,B1IL=mgsinθ+fm①mgsinθ=B2IL+fm②联立可得:fm=mgsinθ.安培力和牛顿第二定律的结合3.图3-4-7据报道,最近已研制出一种可投入使用的电磁轨道炮,其原理如图3-4-7所示.炮弹(可视为长方形导体)置于两固定的平行导轨之间,并与轨道壁密接.开始时炮弹在导轨的一端,通以电流后炮弹会被磁力加速,最后从位于导轨另一端的出口高速射出.设两导轨之间的距离W=0.10m,导轨长L=5.0m,炮弹质量m=0.30kg.导轨上的电流I的方向如图中箭头所示.可以认为,炮弹在轨道内运动时,它所在处磁场的磁感应强度始终为B=2.0T,方向垂直于纸面向里.若炮弹出口速度为v=2.0×103m/s,求通过导轨的电流I.忽略摩擦力与重力的影响.答案6×104A解析在导轨通有电流I时,炮弹作为导体受到磁场施加的安培力为F=IBW①设炮弹的加速度的大小为a,则有F=ma②炮弹在两导轨间做匀加速运动,因而v2=2aL③联立①②③代入题给数据得:I=0.6×105A故通过导轨的电流I=6×104A.(时间:60分钟)题组一通电导线在磁场中的平衡1.图3-4-8如图3-4-8所示条形磁铁放在水平面上,在它的上方偏右处有一根固定的垂直纸面的直导线,当直导线中通以图示方向的电流时,磁铁仍保持静止.下列结论正确的是()A.磁铁对水平面的压力减小B.磁铁对水平面的压力增大C.磁铁对水平面施加向左的静摩擦力D.磁铁所受的合外力增加答案BC2.图3-4-9如图3-4-9所示,金属棒MN两端由等长的轻质细线水平悬挂,处于竖直向上的匀强磁场中,棒中通以由M向N的电流,平衡时两悬线与竖直方向夹角均为θ,如果仅改变下列某一个条件,θ角的相应变化情况是()A.棒中的电流变大,θ角变大B.两悬线等长变短,θ角变小C.金属棒质量变大,θ角变大D.磁感应强度变大,θ角变小答案A3.图3-4-10如图3-4-10所示,在倾角为α的光滑斜面上,放置一根长为L,质量为m,通过电流为I的导线,若使导线静止,应该在斜面上施加匀强磁场B的大小和方向可能为()A.B=,方向垂直于斜面向下B.B=,方向垂直于斜面向上C.B=,方向竖直向下D.B=,方向水平向右答案AC解析根据电流方向和所给定磁场方向的关系,可以确定通电导线所受安培力分别如图所示.又因为导线还受重力G和支持力FN,根据力的平衡知,只有A、C两种情况是可能的,其中A中F=mgsinα,则B=,C中F=mgtanα,B=.4.图3-4-11如图3-4-11所示,挂在天平底部的矩形线圈abcd的一部分悬在匀强磁场中,当给矩形线圈通入如图所示的电流I时,调节两盘中的砝码,使天平平衡.然后使电流I反向,这时要在天平的左盘上加质量为2×10-2kg的砝码,才能使天平重新平衡.求磁场对bc边作用力的大小.若已知矩形线圈共10匝,通入的电流I=0.1A,bc边长度为10cm,求该磁场的磁感应强度.(g取10m/s2)答案0.1N1T解析根据F=BIL可知,电流反向前后,磁场对bc边的作用力大小相等,设为F,但由左手定则可知它们的方向是相反的.电流反向前,磁场对bc边的作用力向上,电流反向后,磁场对bc边的作用力向下.因而有2F=2×10-2×10N=0.2N,所以F=0.1N,即磁场对bc边的作用力大小是0...