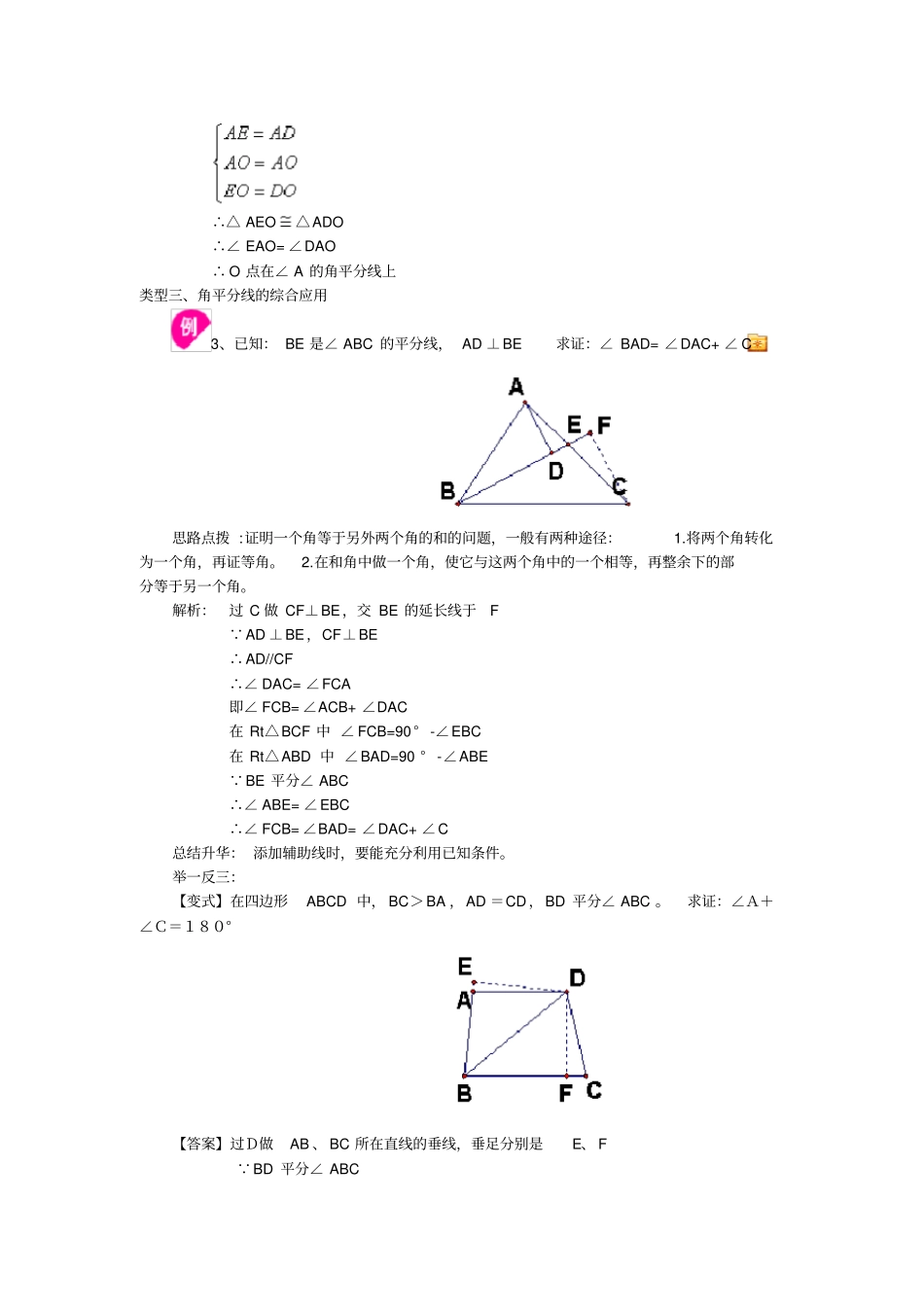
经典例题透析类型一:角平分线性质的应用1、如图,△ABC中∠C=90°,AD平分∠BAC,点D在BC上,且BC=24,CD:DB=3:5求:D到AB的距离。思路点拨:点到直线的距离是经过该点做直线的垂线,该点与垂足之间线段的长度。解析:过D作DE⊥AB于E。∵AD平分∠BAC,DE⊥AB,DC⊥AC∴DE=CD∵BC=24,CD:DB=3:5∴CD=24×=9=DE即点D到AB的距离是9。总结升华:角平分线上的点到角两边的距离相等。举一反三:【变式】如图,∠ACB=90°,BD平分∠ABC交AC于D,DE⊥AB于E,ED的延长线交BC的延长线于F.求证:AE=CF【答案】∵BD平分∠ABC,DE⊥AB,DC⊥BF∴DE=DC在△ADE和△FCD中∴△ADE△FCD(ASA)∴AE=CF类型二:角平分线的判定2、已知,如图,CE⊥AB,BD⊥AC,∠B=∠C,BF=CF。求证:AF为∠BAC的平分线。思路点拨:由已知条件与待求证的结论,应想到角平分线的判定定理。解析:∵CE⊥AB,BD⊥AC(已知)∴∠CDF=∠BEF=90°∵∠DFC=∠BFE(对顶角相等)BF=CF(已知)∴△DFC≌△EFB(AAS)∴DF=EF(全等三角形对应边相等)∵FE⊥AB,FD⊥AC(已知)∴点F在∠BAC的平分线上(到一个角的两边距离相等的点在这个角的平分线上)即AF为∠BAC的平分线总结升华:应用角平分线定理及逆定理时不要遗漏了“垂直”的条件。如果遗漏了说明没有认识到“垂直”条件在证明结论的必要性。举一反三:【变式】如图,已知AB=AC,AD=AE,DB与CE相交于O(1)若DB⊥AC,CE⊥AB,D,E为垂足,试判断点O的位置及OE与OD的大小关系,并证明你的结论。(2)若D,E不是垂足,是否有着同样的结论?并证明你的结论。【答案】(1)∵AB=AC,AD=AE∴BE=CD∵DB⊥AC,CE⊥AB,∴∠BEO=∠CDO=90°在△BEO和△CDO中∴△BEO△CDO∴EO=DO∵EO⊥AB,DO⊥AC∴点O在∠A的平分线上(2)点D,E不是垂足时,(1)的结论仍然成立,连接AO在△ABD和△ACE中∴△ABD△ACE∴∠B=∠C∵AB=AC,AD=AE∴EB=CD在△BEO和△CDO中∴△BEO△CDO∴EO=DO在△AEO和△ADO中∴△AEO△ADO∴∠EAO=∠DAO∴O点在∠A的角平分线上类型三、角平分线的综合应用3、已知:BE是∠ABC的平分线,AD⊥BE求证:∠BAD=∠DAC+∠C思路点拨:证明一个角等于另外两个角的和的问题,一般有两种途径:1.将两个角转化为一个角,再证等角。2.在和角中做一个角,使它与这两个角中的一个相等,再整余下的部分等于另一个角。解析:过C做CF⊥BE,交BE的延长线于F∵AD⊥BE,CF⊥BE∴AD//CF∴∠DAC=∠FCA即∠FCB=∠ACB+∠DAC在Rt△BCF中∠FCB=90°-∠EBC在Rt△ABD中∠BAD=90°-∠ABE∵BE平分∠ABC∴∠ABE=∠EBC∴∠FCB=∠BAD=∠DAC+∠C总结升华:添加辅助线时,要能充分利用已知条件。举一反三:【变式】在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC。求证:∠A+∠C=180°【答案】过D做AB、BC所在直线的垂线,垂足分别是E、F∵BD平分∠ABC∴DE=DF又∵AD=CD∴△AED△CDF(HL)∴∠C=∠DAE又∵∠BAD+∠DAE=180°∴∠C+∠BAD=180°