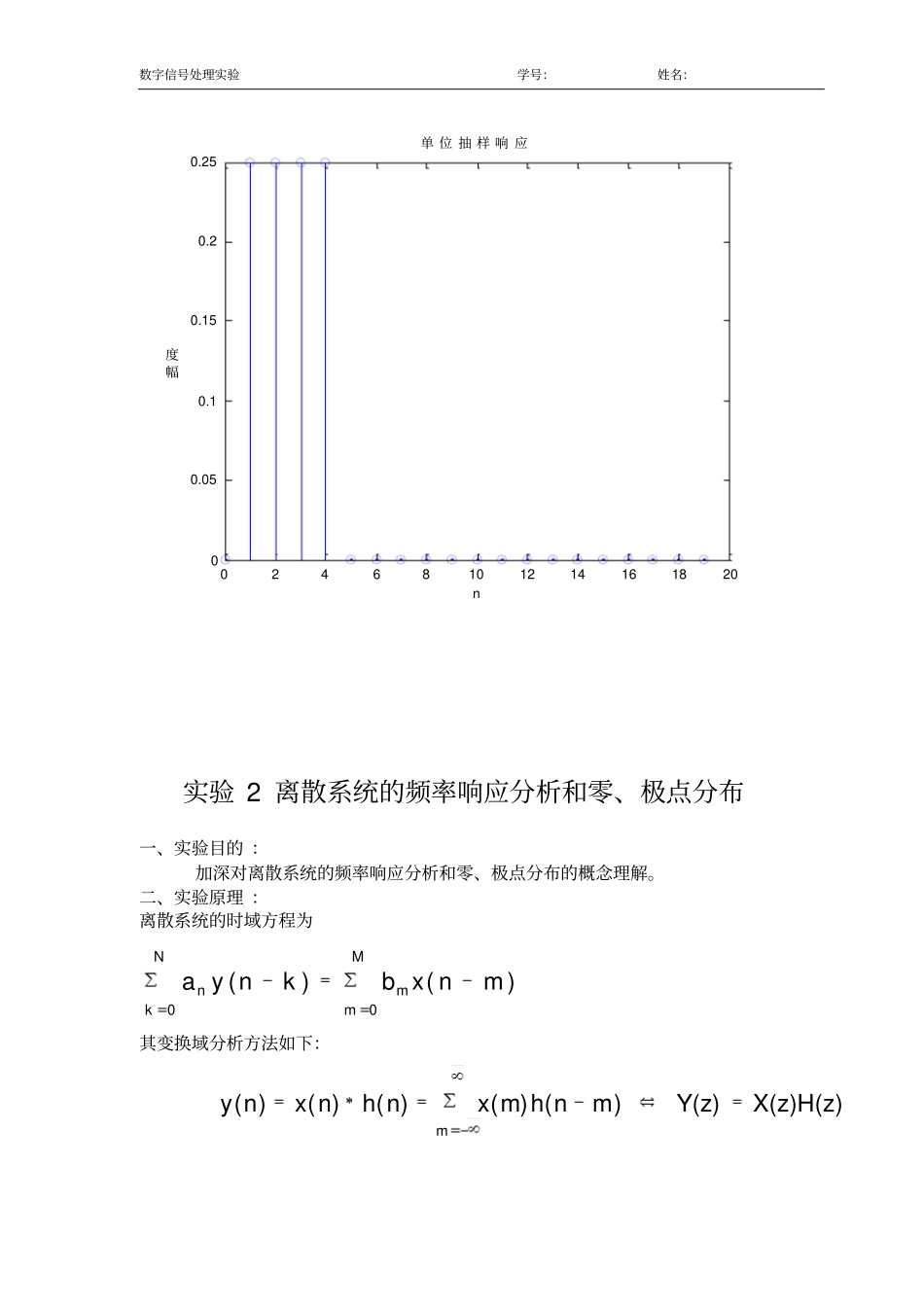
数字信号处理实验学号:姓名:实验1离散系统的时域分析一、实验目的:加深对离散系统的差分方程、单位抽样响应和卷积分析方法的理解。二、实验原理:离散系统其输入、输出关系可用以下差分方程描述:MmmNknmnxbknya00)()(输入信号分解为冲激信号,mmnmxnx)()()(系统单位抽样序列h(n),则系统响应为如下的卷积计算式:mmnhmxnhnxny)()()()()(当00aNkak,...2,1,0时,h(n)是有限长度的(n:[0,M]),称系统为FIR系统;反之,称系统为IIR系统。三、实验内容编制程序求解下列两个系统的单位抽样响应,并绘出其图形。(1))1()()2(125.0)1(75.0)(nxnxnynyny(2))4()3()2()1([25.0)(nxnxnxnxny(1)源程序:N=21;b=[1-1];a=[10.750.125];Discrete-timesystmex(n)y(n)数字信号处理实验学号:姓名:x=[1zeros(1,N-1)];n=0:1:N-1;y=filter(b,a,x);stem(n,y);xlabel('n');ylabel('幅度');title('单位抽样响应');图形:02468101214161820-2-1.5-1-0.500.511.5n幅度单位抽样响应(2)源程序:N=20;d=[00.250.250.250.25];c=[1];x=[1zeros(1,N-1)];n=0:1:N-1;y=filter(d,c,x);stem(n,y);xlabel('n');ylabel('幅度');title('单位抽样响应');图形如下:数字信号处理实验学号:姓名:0246810121416182000.050.10.150.20.25n幅度单位抽样响应实验2离散系统的频率响应分析和零、极点分布一、实验目的:加深对离散系统的频率响应分析和零、极点分布的概念理解。二、实验原理:离散系统的时域方程为MmmNknmnxbknya00)()(其变换域分析方法如下:X(z)H(z)Y(z))()()()()(mmnhmxnhnxny数字信号处理实验学号:姓名:系统函数为NNMMzazaazbzbbzXzYzH......)()()(110110分解因式NkkMmmNkkkMmmmzdzcKzazbzH111100)1()1()(,其中mc和kd称为零、极点。在MATLAB中,可以用函数[z,p,K]=tf2zp(num,den)求得有理分式形式的系统函数的零、极点,用函数zplane(z,p)绘出零、极点分布图;也可以用函数zplane(num,den)直接绘出有理分式形式的系统函数的零、极点分布图。使h=freqz(num,den,w)函数可求系统的频率响应,w是频率的计算点,如w=0:pi/255:pi,h是复数,abs(h)为幅度响应,angle(h)为相位响应。另外,在MATLAB中,可以用函数[r,p,k]=residuez(num,den)完成部分分式展开计算;可以用函数sos=zp2sos(z,p,K)完成将高阶系统分解为2阶系统的串联。三、实验内容练习1求下列直接型系统函数的零、极点,并将它转换成二阶节形式解用MATLAB计算程序如下:num=[1-0.1-0.3-0.3-0.2];den=[10.10.20.20.5];[z,p,k]=tf2zp(num,den);disp('零点');disp(z);disp('极点');disp(p);disp('增益系数');disp(k);sos=zp2sos(z,p,k);disp('二阶节');disp(real(sos));zplane(num,den)输入到“num”和“den”的分别为分子和分母多项式的系数。计算求得零、极点增益系数和二阶节的系数:零点0.9615-0.5730-0.1443+0.5850i数字信号处理实验学号:姓名:-0.1443-0.5850i极点0.5276+0.6997i0.5276-0.6997i-0.5776+0.5635i-0.5776-0.5635i增益系数1二阶节1.0000-0.3885-0.55091.00001.15520.65111.00000.28850.36301.0000-1.05520.7679系统函数的二阶节形式为:极点图如右图。2差分方程)3(02.0)2(36.0)1(44.0)(8.0)3(6.0)2(45.0)1(7.0)(nxnxnxnxnynynyny所对应的系统的频率响应。解:差分方程所对应的系统函数为3213216.045.07.0102.036.044.08.0)(zzzzzzzH用MATLAB计算的程序如下:数字信号处理实验学号:姓名:k=256;num=[0.8-0.440.360.02];den=[10.7-0.45-0.6];w=0:pi/k:pi;h=freqz(num,den,w);subplot(2,2,1);plot(w/pi,real(h));gridtitle('实部')xlabel('\omega/\pi');ylabel('幅度')subplot(2,2,2);plot(w/pi,imag(h));gridtitle('虚部')xlabel('\omega/\pi');ylabel('Amplitude')subplot(2,2,3);plot(w/pi,abs(h));gridtitle('幅度谱')xlabel('\omega/\pi');ylabel('幅值')subplot(2,2,4);plot(w/pi,angle(h));gridtitle('相位谱')xlabel('\omega/\pi');ylabel('弧度')数字信号处理实验学号:姓名:3求系统12345123450.05280.07970.12950.12950.07970.0528()11.81072.49471.88010.95370.2336zzzzzHzzzzzz的零、极...