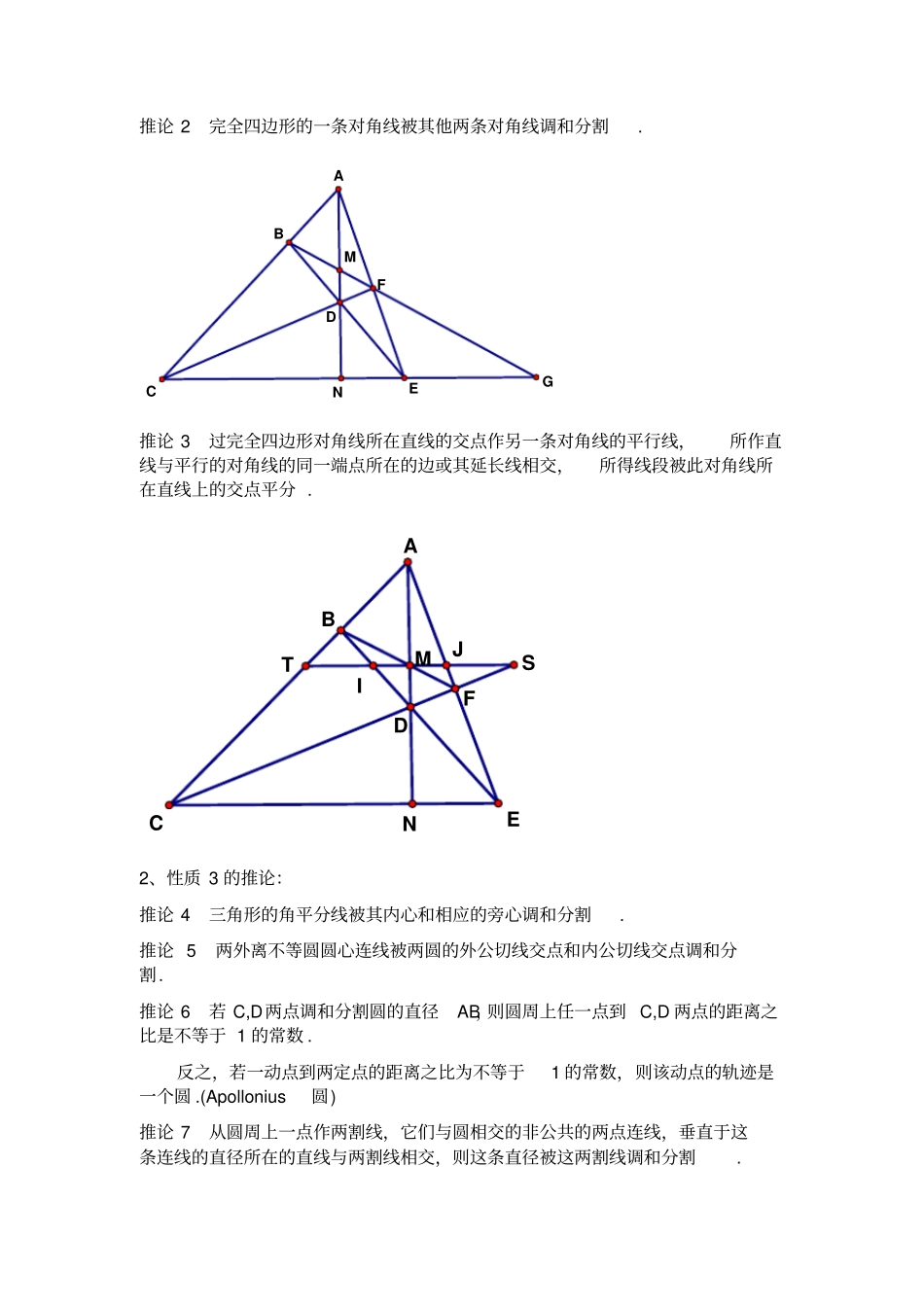
调和点列(一)一、线段调和分割的基本概念如果线段AB被两点C,D内分与外分成同一比例,则称线段AB被点C和D调和分割.亦称点列A,B;C,D为调和点列.显然,当C,D调和分割AB时,也可称A、B两点调和分割CD.有时也称点C和D是线段AB的调和共轭点.若从共点直线外任一点P作射线PA,PC,PB,PD,则可称射线束为调和线束,且PA与PB共轭,PC与PD共轭.二、调和点列的性质调和点列联系了众多的图形,因而它有一系列有趣的性质.性质1设A,C,B,D是共线四点,点M为AB中点,则C,D调和分割线段AB的充要条件是满足下述六个条件之一.(1)点AB调和分割CD.(2)112ACADAB.(3)22ABCDADBCACDB.(4)CACBCMCD.(5)DADBDMDC.(6)22MAMBMCMD.CDMAB性质2设A,C,B,D是共线四点,过共点直线外一点P引射线PA,PC,PB,PD,则C,D调和分割线段AB的充要条件是满足下述两个条件之一.(1)线束PA,PC,PB,PD,其中一射线的任意平行线被其他三条射线截出相等的两线段.(2)另一直线l分别交射线PA,PC,PB,PD于点A’,C’,B’,D’时,点C’,D’调和分割线段A’B’.lA'C'B'D'DCABP性质3对线段AB的内分点C和外分点D,以及直线AB外一点P,给出如下四个论断:①PC是∠APB的平分线.②PD是∠APB的外角平分线.③C,D调和分割线段AB.④PC⊥PD.以上四个论断中,任选两个作题设,另两个作结论组成的六个命题均为真命题.DCABP性质4三角形的一边被其边上的内(旁)切圆的切点和另一点调和分割的充要条件是,另一点与其余两边上的两个切点三点共线.性质5从圆O外一点A引圆的割线交圆O于C,D,若割线ACD与点A的切点弦交于点B,则弦CD被A,B调和分割.三、几个推论1、性质2的推论:推论1梯形的两腰延长线的交点和两对角线的交点调和分割两底中点的连线.MDFNACEB推论2完全四边形的一条对角线被其他两条对角线调和分割.MGFDACENB推论3过完全四边形对角线所在直线的交点作另一条对角线的平行线,所作直线与平行的对角线的同一端点所在的边或其延长线相交,所得线段被此对角线所在直线上的交点平分.SJITMFDACENB2、性质3的推论:推论4三角形的角平分线被其内心和相应的旁心调和分割.推论5两外离不等圆圆心连线被两圆的外公切线交点和内公切线交点调和分割.推论6若C,D两点调和分割圆的直径AB,则圆周上任一点到C,D两点的距离之比是不等于1的常数.反之,若一动点到两定点的距离之比为不等于1的常数,则该动点的轨迹是一个圆.(Apollonius圆)推论7从圆周上一点作两割线,它们与圆相交的非公共的两点连线,垂直于这条连线的直径所在的直线与两割线相交,则这条直径被这两割线调和分割.推论8一已知圆的直径被另一圆周调和分割的充要条件是,已知直径的圆周与过两分割点的圆周正交(即交点处切线相互垂直).FODCABO1推论9设点C是△AEF的内心,角平分线AC交边EF于点B,射线AB交△AEF的外接圆圆O2于点O,则射线AB上的点D为△AEF的旁心的充要条件是ACDOCBOB.推论10设△AEF的角平分线AB交EF于点B,交△AEF的外接圆于点O,则22OEOFOAOB.3、性质4的推论:推论11若凸四边形有内切圆,则相对边上的两切点所在直线与凸四边形一边延长线的交点和这一边上的内切圆切点调和分割这一边.4、性质5的推论:推论12从圆O外一点A引圆的两条割线交圆于四点,以这四点为顶点的四边形的对角线相交于点B,设直线AB交圆O于C,D,则A,B调和分割CD弦.CDBFGOAHE四、调和点列的性质应用例1如图,过圆外一点P作圆的两条切线PA,PB,A,B为切点,再过点P作圆的一条割线分别交圆于C,D两点,过切点B作PA的平行线分别交直线AC,AD于E,F,求证:BE=BF.(2005年第5届中国西部数学奥林匹克题)FECBAPD例2如图,在△ABC中,AD⊥BC,H为AD上任意一点,CH,BH分别与AB,AC交于点E,F,求证:∠EDA=∠FDA.(第18届普特南B.1)(1987年友谊杯国际竞赛)(第14届爱尔兰奥林匹克)(第26届加拿大奥林匹克)EFDABCH例3如图,在△PBC中,∠PBC=60°,过点P作△PBC的外接圆圆O的切线,与CB的延长线交于点A.点D,E分别在线段PA和圆O上,使得∠DBE=90°,PD=PE,连接BE与PC相交于点F.已知AF,BP,CD三线共点.(1)求证:BF是∠PBC的平分线.(2)求tan∠PCB的值.(2006年西部数学奥林匹克题)FDEAOPBC例4如图,已知A为圆O外一点,过A引圆O的割线交圆O于点B,C,且点B在线段...