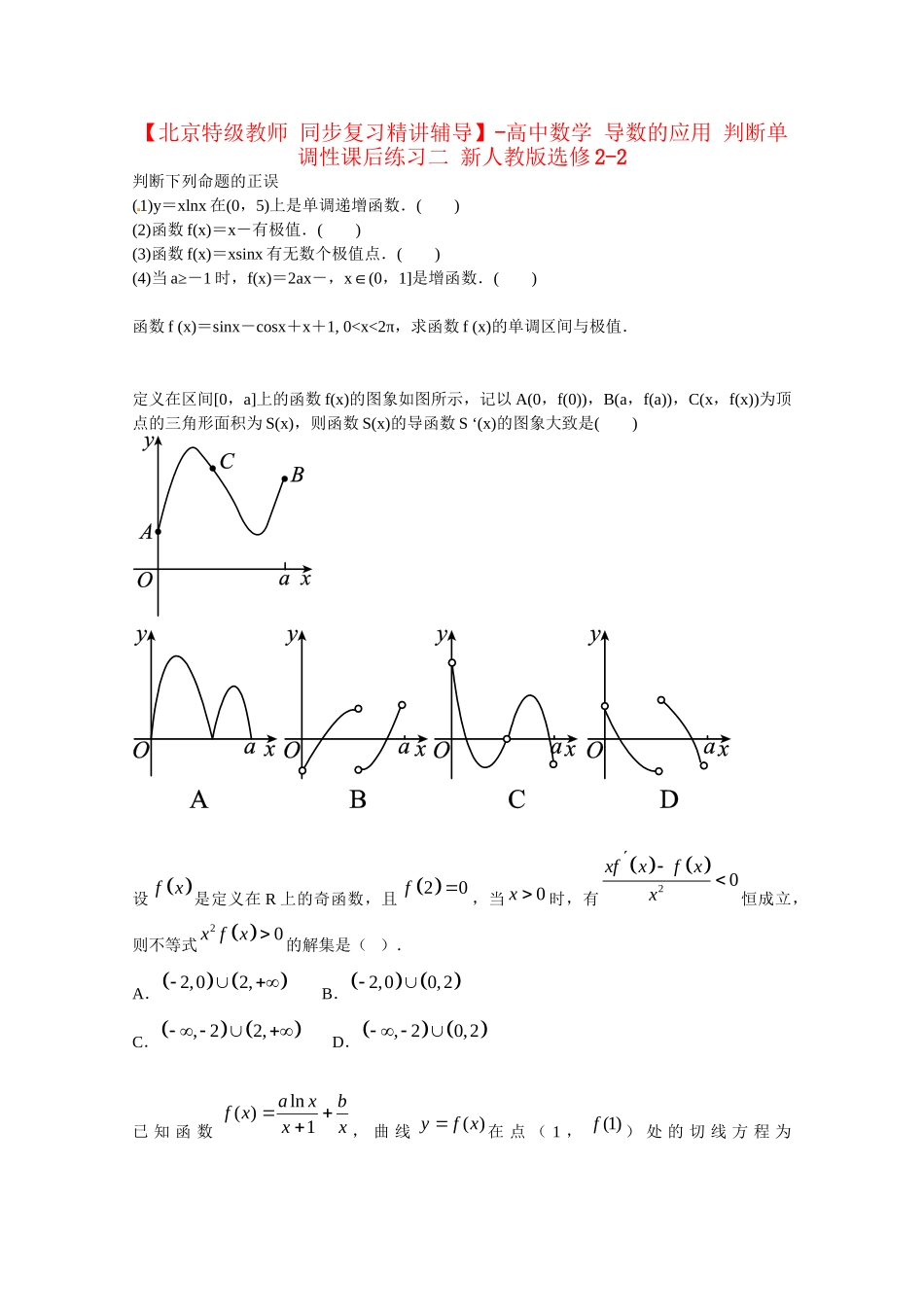
【北京特级教师同步复习精讲辅导】-高中数学导数的应用判断单调性课后练习二新人教版选修2-2判断下列命题的正误(1)y=xlnx在(0,5)上是单调递增函数.()(2)函数f(x)=x-有极值.()(3)函数f(x)=xsinx有无数个极值点.()(4)当a≥-1时,f(x)=2ax-,x∈(0,1]是增函数.()函数f(x)=sinx-cosx+x+1,00).(1)若m=1,求曲线y=f(x)在点(2,f(2))处的切线方程;(2)若函数f(x)在区间(2m-1,m+1)上单调递增,求实数m的取值范围.课后练习详解答案:错误;错误;正确;正确.详解:(1)要特别注意函数的定义域,函数的定义域为(0∞,+).因为y‘=lnx+1,令y‘>0,得x>;令y‘<0,得01,所以f(x)在(∞-,0)和(0∞,+)上是单调递增函数,没有极值.(3)f‘(x)=sinx+xcosx,令f‘(x)=0,当cosx≠0时,有tanx=-x,作出函数y=tanx与y=-x的图象(图略),可知方程tanx=-x有无数个解,所以函数f(x)=xsinx有无数个极值点.(4)f‘(x)=2a+,因为y=在(0,1]上是减函数,所以≥2,又a≥-1,所以f‘(x)≥-2+2=0,所以f(x)在(0,1]上是增函数.答案:单调区间f(x)的单调递增区间是(0,π)和,单调递减区间是;极小值为f=,极大值为f(π)=π+2.详解:由f(x)=sinx-cosx+x+1,0