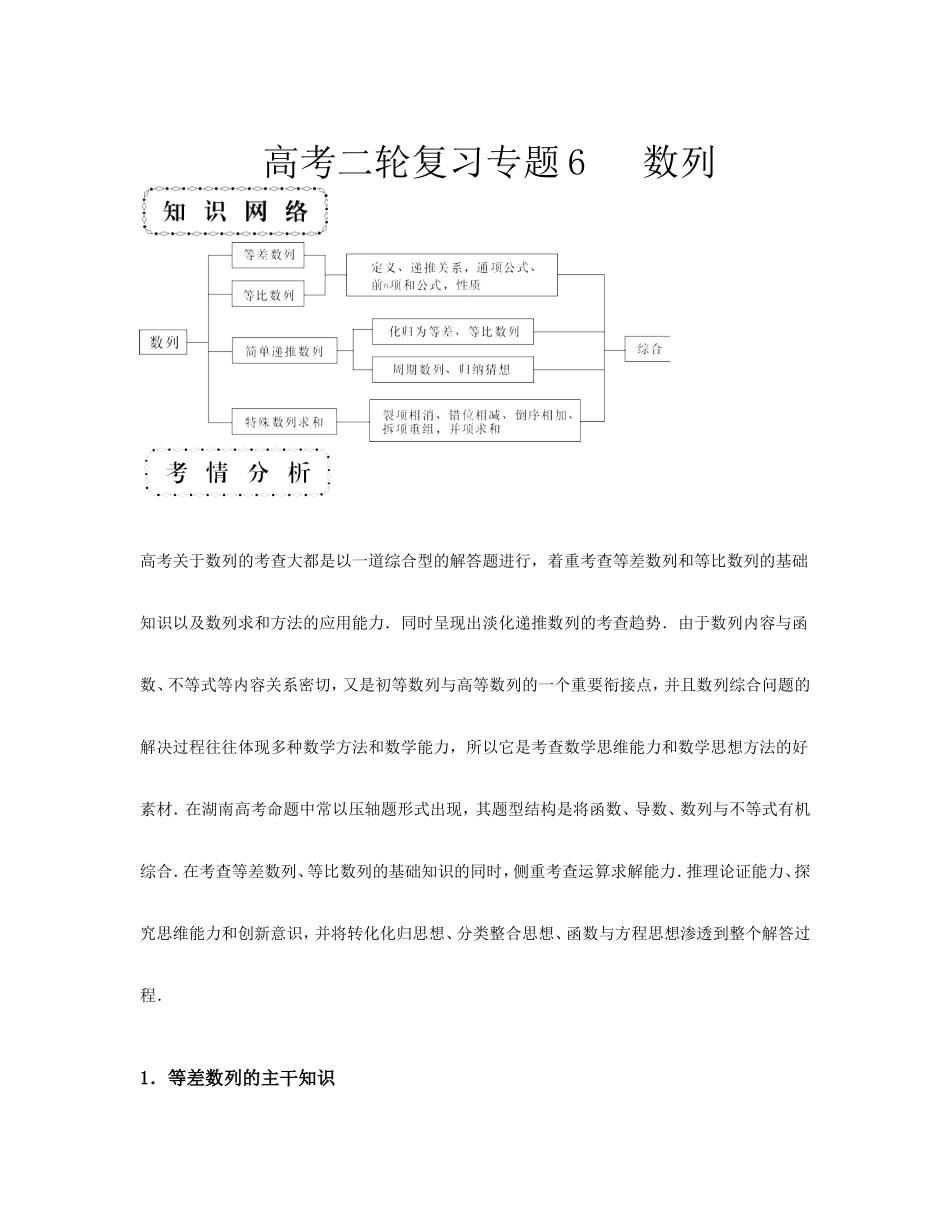
高考二轮复习专题6数列高考关于数列的考查大都是以一道综合型的解答题进行,着重考查等差数列和等比数列的基础知识以及数列求和方法的应用能力.同时呈现出淡化递推数列的考查趋势.由于数列内容与函数、不等式等内容关系密切,又是初等数列与高等数列的一个重要衔接点,并且数列综合问题的解决过程往往体现多种数学方法和数学能力,所以它是考查数学思维能力和数学思想方法的好素材.在湖南高考命题中常以压轴题形式出现,其题型结构是将函数、导数、数列与不等式有机综合.在考查等差数列、等比数列的基础知识的同时,侧重考查运算求解能力.推理论证能力、探究思维能力和创新意识,并将转化化归思想、分类整合思想、函数与方程思想渗透到整个解答过程.1.等差数列的主干知识(1)等差数列的通项公式an=a1+(n-1)d和an=am+(n-m)d.(2)等差数列的公差d=和d=.(3)等差数列的前n项和公式:①Sn===…;②Sn=na1+d;③Sn=An2+Bn(A、B为常数).(4)等差数列的性质①m、n、p、q∈N*,若m+n=p+k,则am、an、ap、ak的关系为am+an=ap+ak,特别地a1+an=a2+an-1=….②an=pn+k(p,k是常数)是{an}成等差数列的充要条件,(n,an)是某直线上的一群孤立的点.③数列{an}的前n项和Sn=An2+Bn是{an}成等差数列的充要条件.④若{an}和{bn}均是等差数列,则{man+kbn}仍为等差数列,其中m,k为常数.⑤等差数列中依次k项和成等差数列,即Sk、S2k-Sk、S3k-S2k、…,成等差数列,公差为k2d.2.等比数列的主干知识(1)等比数列的通项公式为an=a1qn-1和an=amqn-m,(2)等比数列的前n项和公式Sn=(3)等比数列的性质①m、n、p、q∈N*,若m+n=p+k,则am、an、ap、ak的关系为aman=apak,特别地a1an=a2an-1=….②若{an}和{bn}均是等比数列,则{manbn}仍为等比数列,其中m为非零常数.③等比数列中依次k项和成等比数列,即Sk、S2k-Sk、S3k-S2k、…,成等比数列,其公比为qk.④等比数列中依次k项积成等比数列,记Tn为前n项积,则Tk、、、…成等比数列,其公比为1.求数列通项的常见方法:(1)累加(乘)法:形如an+1-an=f(n)或=f(n);(2)构造等差或等比数列:如:①an+1=pan+q(p,q为常数,p≠0,p≠1,q≠0),变形为an+1+=p(an+);②an+1=pan+f(n)(p为常数,p≠0),转化为an+1+g(n+1)=p(an+g(n)).③a1=a,a2=b,an+2=pan+1+qan,转化为an+2-Aan+1=B(an+1-Aan),用待定系数法求A、B,从而转化为等比数列求解.2.2.求数列前n项和的常用方法(1)公式法:直接由等差数列、等比数列求和公式;(2)错位相减法:数列{anbn}中,一个为等差数列,一个为等比数列,则其前n项和Sn可用错位相减法;(3)裂项相消法:将数列中的通项拆成两项之差,使和式中部分项可相互抵消,从而化简和式;(4)除上述较常用的方法之外,还有①分组求和法;②并项求和法;③倒序相加法等.一、【高考真题--热身感悟】1.(2011·北京)在等比数列{an}中,若a1=,a4=-4,则公比q=________;|a1|+|a2|+…+|an|=________.2.(2014江苏)在各项均为正数的等比数列中,,则的值是_______.3.(2011·课标全国)等比数列{an}的各项均为正数,且2a1+3a2=1,a=9a2a6.(1)求数列{an}的通项公式;(2)设bn=log3a1+log3a2+…+log3an,求数列的前n项和.4.已知当x=5时,二次函数f(x)=ax2+bx取得最小值,等差数列{an}的前n项和Sn=f(n),a2=-7.(1)求数列{an}的通项公式;(2)数列{bn}的前n项和为Tn,且bn=,求Tn.典例精析:1、等差、等比数列的基本公式及应用:例1.1){an}为等差数列,Sn为其前n项和,a7=5,S7=21,则S10=()A40B35C30D282)(2014辽宁卷)设等差数列{an}的公差为d,若数列{}为递减数列,则()Ad<0Bd>0Ca1d<0Da1d>03)已知{an}是首项为1的等比数列,Sn是{an}的前n项和,且9S3=S6,则数列的前5项和为()2、等差、等比数列的基本性质及应用:例21)(2014北京)若等差数列满足,,则当________时的前项和最大。2)已知等差数列{an},{bn}的前n项和分别为Sn和Tn,若,且是整数,则n的值为___________.3)各项均为正数的等比数列{an}满足a1a7=4,a6=8,若函数f(x)=a1x+a2x2+a3x3+...+a10x10的导数为f`(x),则f`()=3、等差、等比数列的综合应用:例4(2014上海)已知数列满足.(1)若,求的取值范围;(2)若是公比为等比数列,,求的取值范围;(3)若成等差数列,且,求正整数的最大值,以及取最大值时相应数列的公差.