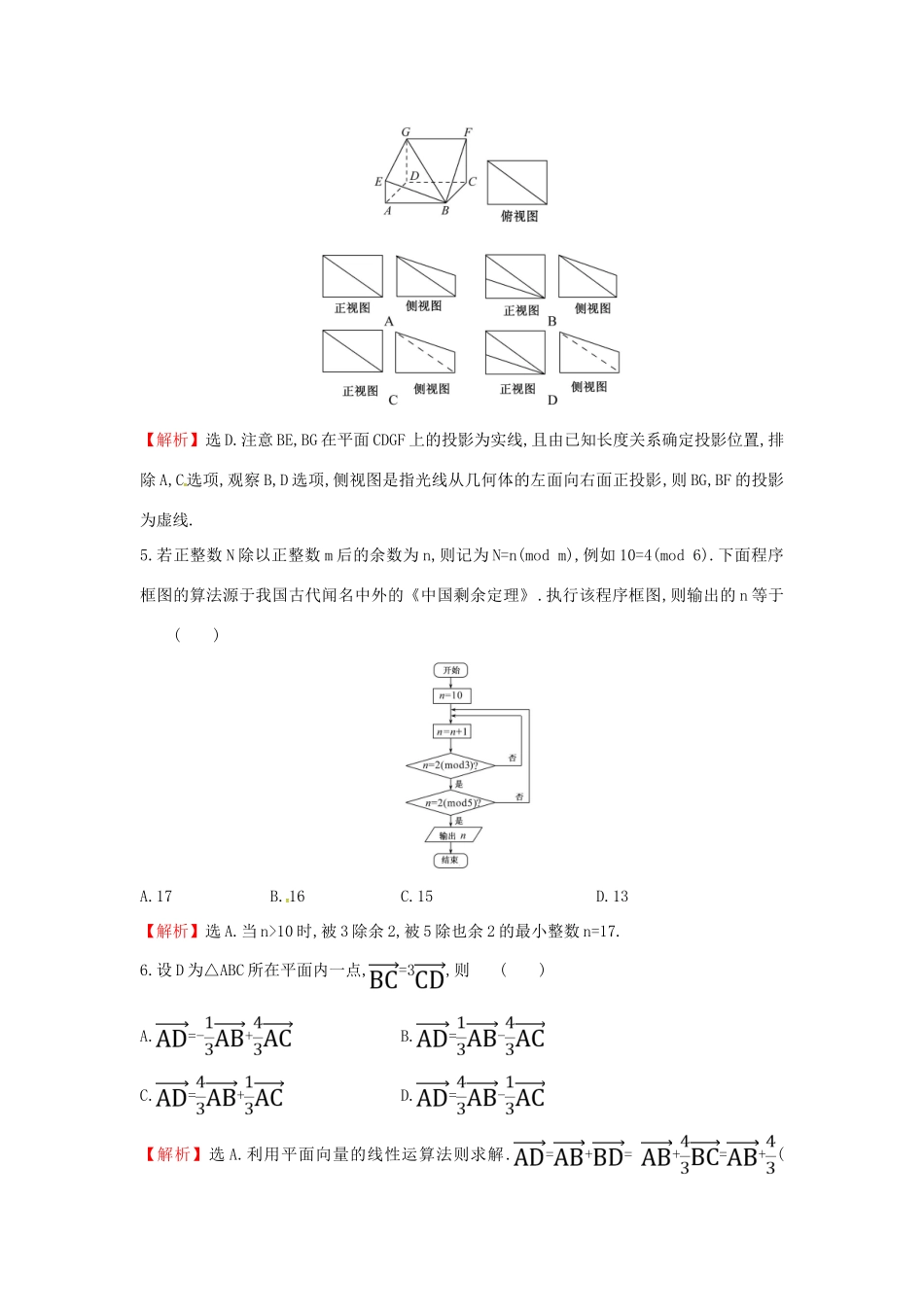
标准仿真模拟练(二)(120分钟150分)第Ⅰ卷一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合要求的)1.已知集合A={x|y=ln(x+3)},B={x|x≥2},则下列结论正确的是()A.A=BB.A∩B=C.A⊆BD.B⊆A【解析】选D.由题意得A={x|x>-3},B={x|x≥2},结合数轴可得:B⊆A.2.当-10,1+m>0,所以z对应的点位于第一象限.3.设m,n是不同的直线,α,β是不同的平面,下列说法中正确的是()A.若m∥α,n⊥β,m⊥n,则α⊥βB.若m∥α,n⊥β,m∥n,则α⊥βC.若m∥α,n⊥β,m⊥n,则α∥βD.若m∥α,n⊥β,m∥n,则α∥β【解析】选B.若m∥α,n⊥β,m⊥n,则α与β可能平行,也可能相交,选项A,C错;由条件n⊥β,m∥n推出m⊥β,又m∥α,则α⊥β,选项B正确,选项D错.4.如图,多面体ABCD-EFG的底面ABCD为正方形,FC=GD=2EA,其俯视图如下,则其正视图和侧视图正确的是()【解析】选D.注意BE,BG在平面CDGF上的投影为实线,且由已知长度关系确定投影位置,排除A,C选项,观察B,D选项,侧视图是指光线从几何体的左面向右面正投影,则BG,BF的投影为虚线.5.若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如10=4(mod6).下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于()A.17B.16C.15D.13【解析】选A.当n>10时,被3除余2,被5除也余2的最小整数n=17.6.设D为△ABC所在平面内一点,=3,则()A.=-+B.=-C.=+D.=-【解析】选A.利用平面向量的线性运算法则求解.=+=+=+(-)=-+.7.已知sinα+cosα=,则tanα=()A.B.C.-D.-【解析】选A.因为sinα+cosα=,所以(sinα+cosα)2=3,所以sin2α+2sinαcosα+2cos2α=3,所以=3,所以=3.所以2tan2α-2tanα+1=0,即(tanα-1)2=0,所以tanα=.8.给定四条曲线:①x2+y2=,②+=1,③x2+=1,④+y2=1,其中与直线x+y-=0仅有一个交点的曲线是()A.①②③B.②③④C.①②④D.①③④【解析】选D.分析选项可知,四条曲线中有且只有一条曲线不符合要求,故可考虑找不符合条件的曲线从而筛选,而在四条曲线中②是一个面积最大的椭圆,故可先看②,显然直线和曲线+=1是相交的,因为直线上的点(,0)在椭圆内,故②不符合条件.9.若曲线y=x2上存在点(x,y)满足约束条件则实数m的取值范围是()A.[-2,1]B.[1,+∞)C.(0,+∞)D.(-∞,1]【解析】选D.作出不等式组表示的平面区域(如阴影部分),作出抛物线y=x2,解方程组得或即直线x+y-2=0与抛物线y=x2的交点坐标为(1,1)和(-2,4).若曲线y=x2上存在点(x,y)在平面区域内,则m≤1.10.函数f(x)=ln|x|+|sinx|(-π≤x≤π且x≠0)的图象大致是()【解析】选D.函数f(x)为偶函数,排除A;当x>0时,f(x)=lnx+sinx,f′(x)=+cosx,当x∈时,f′(x)>0,函数f(x)在递增,排除C;f″(x)=--sinx<0,所以,f′(x)在(0,π)内单调递减,所以,函数f(x)在(0,π)内先增后减.11.平面直角坐标系xOy中,双曲线C1:-=1(a>0,b>0)的渐近线与抛物线C2:x2=2py(p>0)交于点O,A,B.若△OAB的垂心为C2的焦点,则C1的离心率为()A.B.C.2D.【解析】选A.由题意,不妨设直线OA的方程为y=x,直线OB的方程为y=-x.由得x2=2p·x,所以x=,y=,所以A.设抛物线C2的焦点为F,则F,所以kAF=.因为△OAB的垂心为F,所以AF⊥OB,所以kAF·kOB=-1,所以·=-1,所以=.设C1的离心率为e,则e2===1+=.所以e=.12.若方程|x2-2x-1|-t=0有四个不同的实数根x1,x2,x3,x4,且x1