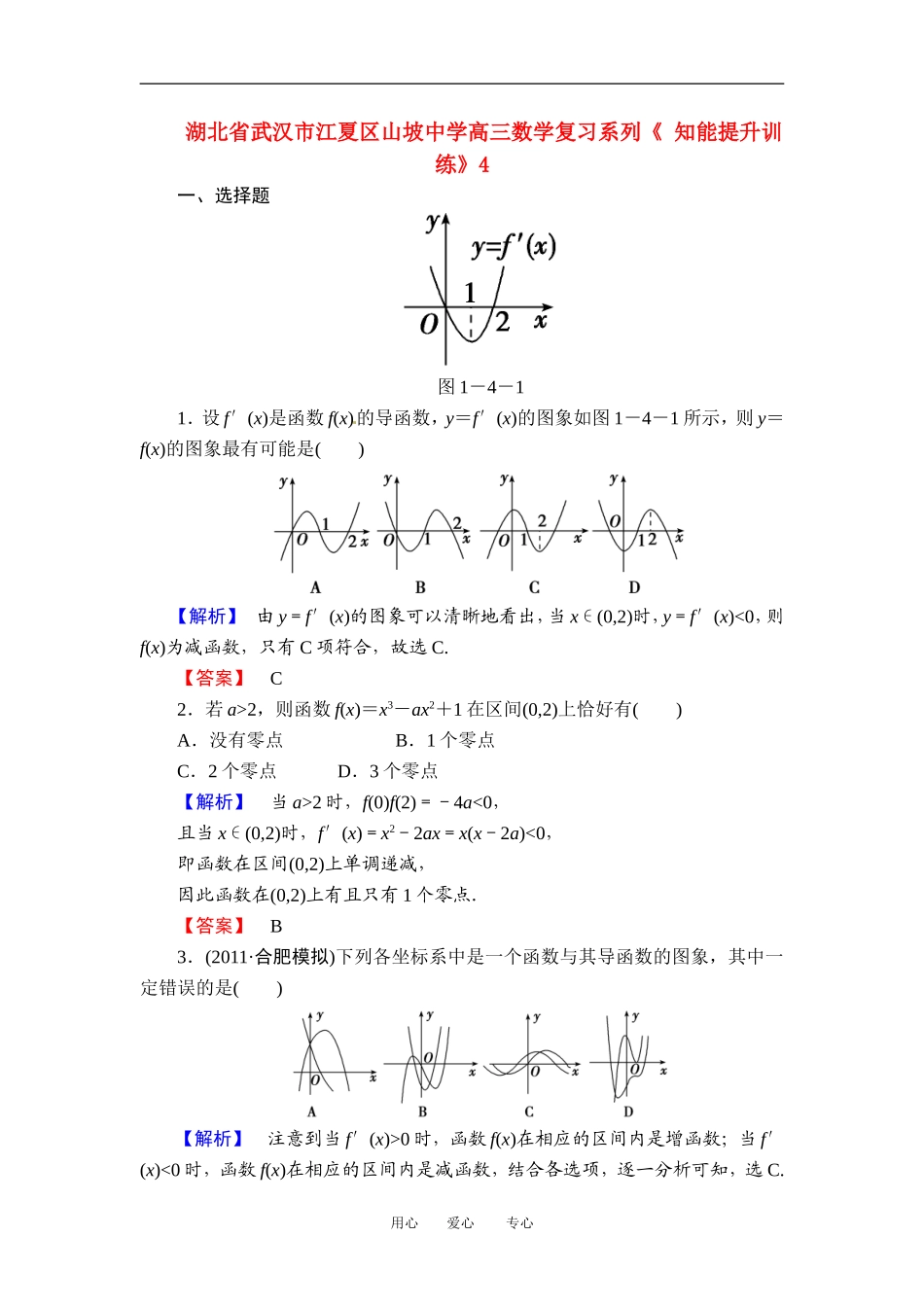
湖北省武汉市江夏区山坡中学高三数学复习系列《知能提升训练》4一、选择题图1-4-11.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图1-4-1所示,则y=f(x)的图象最有可能是()【解析】由y=f′(x)的图象可以清晰地看出,当x∈(0,2)时,y=f′(x)<0,则f(x)为减函数,只有C项符合,故选C.【答案】C2.若a>2,则函数f(x)=x3-ax2+1在区间(0,2)上恰好有()A.没有零点B.1个零点C.2个零点D.3个零点【解析】当a>2时,f(0)f(2)=-4a<0,且当x∈(0,2)时,f′(x)=x2-2ax=x(x-2a)<0,即函数在区间(0,2)上单调递减,因此函数在(0,2)上有且只有1个零点.【答案】B3.(2011·合肥模拟)下列各坐标系中是一个函数与其导函数的图象,其中一定错误的是()【解析】注意到当f′(x)>0时,函数f(x)在相应的区间内是增函数;当f′(x)<0时,函数f(x)在相应的区间内是减函数,结合各选项,逐一分析可知,选C.用心爱心专心【答案】C4.函数f(x)=的最大值为()A.eB.C.2eD.【解析】函数f(x)的定义域为(0,+∞),又f′(x)==.令f′(x)=0得x=,且当00,当x>时,f′(x)<0,所以f(x)在x=处取得极大值,也就是函数在定义域上的最大值f()=.【答案】D5.(2011·福建高考)若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于()A.2B.3C.6D.9【解析】f′(x)=12x2-2ax-2b,∵f(x)在x=1处有极值,∴f′(1)=12-2a-2b=0,∴a+b=6.又a>0,b>0,∴a+b≥2,∴2≤6,∴ab≤9,当且仅当a=b=3时等号成立,∴ab的最大值为9.【答案】D二、填空题6.函数f(x)=x+2cosx在区间[0,]上的单调递减区间是__________.【解析】f′(x)=1-2sinx,令f′(x)≤0,即1-2sinx≤0,所以sinx≥.又∵x∈[0,],所以≤x≤,即减区间是[,].【答案】[,]7.设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为__________.【解析】∵f′(x)=g′(x)+2x,∴f′(1)=g′(1)+2,又由已知得g′(1)=2,用心爱心专心∴f′(1)=2+2=4.【答案】48.(2011·南京模拟)若直线y=kx-3与曲线y=2lnx相切,则实数k=__________.【解析】依题意,设切点坐标是(x0,y0),则有由此得2-3=2lnx0,x0=e-,k===2.【答案】2三、解答题9.设函数y=f(x)在(a,b)上的导数为f′(x),f′(x)在(a,b)上的导数为f″(x),若在(a,b)上,f″(x)<0恒成立,则称函数f(x)在(a,b)上为“凸函数”,若函数f(x)=x4-mx3-x2为区间(-1,3)上的“凸函数”,试确定实数m的值.【解】∵f(x)=x4-mx3-x2,∴f′(x)=x3-mx2-3x,∴f″(x)=x2-mx-3.依题意x2-mx-3<0在(-1,3)上恒成立.令g(x)=x2-mx-3,则有,即解得于是m=2,即实数m的值等于2.10.(2011·北京高考)已知函数f(x)=(x-k)ex.(1)求f(x)的单调区间;(2)求f(x)在区间[0,1]上的最小值.【解】(1)f′(x)=(x-k+1)ex.令f′(x)=0,得x=k-1.f(x)与f′(x)的变化情况如下:所以,f(x)的单调递减区间是(-∞,k-1);单调递增区间是(k-1,+∞).(2)当k-1≤0,即k≤1时,函数f(x)在[0,1]上单调递增,所以f(x)在区间[0,1]上的最小值为f(0)=-k;用心爱心专心当0