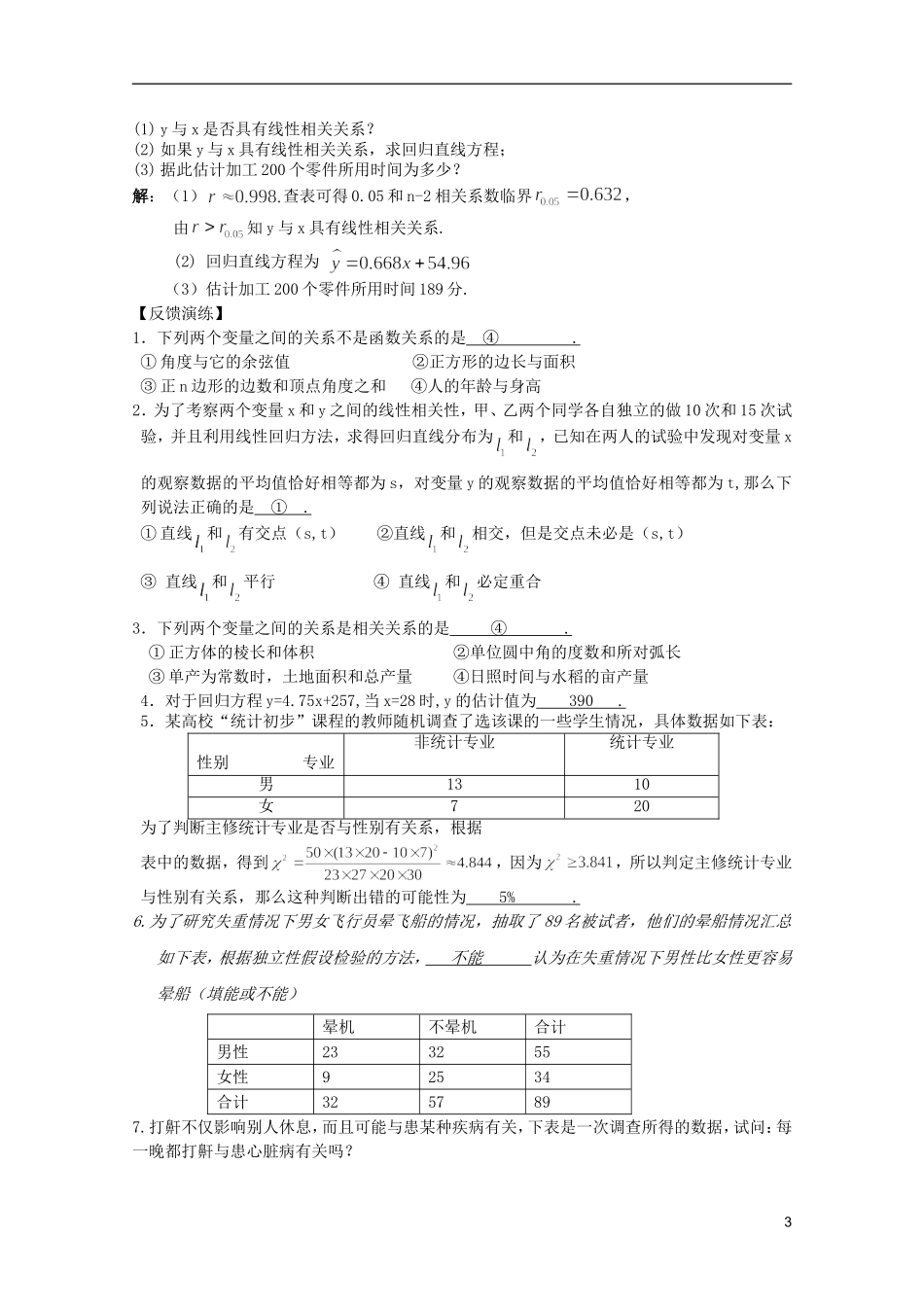
第4课案例分析【考点导读】1.会作两个有关联变量数据的散点图,并利用散点图直观认识变量间的相关关系.2.知道最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.3.了解独立性检验的基本思想、方法及其初步应用,了解回归与分析的基本思想、方法及其初步应用.【基础练习】1.根据下表中的数据:可求出与的线性回归方程是2.线性回归方程表示的直线必经过的一个定点是3.设有一个直线回归方程为,则变量x增加一个单位时③.①y平均增加1.5个单位②y平均增加2个单位③y平均减少1.5个单位④y平均减少2个单位4.对于给定的两个变量的统计数据,下列说法正确的是③.①都可以分析出两个变量的关系②都可以用一条直线近似地表示两者的关系③都可以作出散点图④都可以用确定的表达式表示两者的关系5.对于两个变量之间的相关系数,下列说法中正确的是③.①|r|越大,相关程度越大②|r|,|r|越大,相关程度越小,|r|越小,相关程度越大③|r|1且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小④以上说法都不对【范例解析】例1.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.(1)根据以上数据建立一个2×2的列联表;(2)判断性别与休闲方式是否有关系.解:(1)2×2的列联表性别休闲方式看电视运动总计女432770男213354总计6460124(2)假设“休闲方式与性别无关”计算因为,所以有理由认为假设“休闲方式与性别无关”是不合理的,即有97.5%的把握认为“休闲方式与性别有关”.x-1012y-10111点评对两个变量相关性的研究,可先计算的值,并根据临界表进行估计与判断.例2.以下是某地搜集到的新房屋的销售价格和房屋的面积的数据:(1)画出数据对应的散点图;(2)求线性回归方程,并在散点图中加上回归直线;(3)据(2)的结果估计当房屋面积为时的销售价格解:(1)数据对应的散点图如图所示:(2),,设所求回归直线方程为,则故所求回归直线方程为(3)据(2),当时,销售价格的估计值为:(万元)点评因为y对x呈线性相关关系,所以可以一元线性相关的方法解决问题.例3.一个车间为了为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次实验,测得如下数据:零件数x(个)102030405060708090100加工时间y(分)6268758189951021081151222(1)y与x是否具有线性相关关系?(2)如果y与x具有线性相关关系,求回归直线方程;(3)据此估计加工200个零件所用时间为多少?解:(1)查表可得0.05和n-2相关系数临界,由知y与x具有线性相关关系.(2)回归直线方程为(3)估计加工200个零件所用时间189分.【反馈演练】1.下列两个变量之间的关系不是函数关系的是④.①角度与它的余弦值②正方形的边长与面积③正n边形的边数和顶点角度之和④人的年龄与身高2.为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立的做10次和15次试验,并且利用线性回归方法,求得回归直线分布为和,已知在两人的试验中发现对变量x的观察数据的平均值恰好相等都为s,对变量y的观察数据的平均值恰好相等都为t,那么下列说法正确的是①.①直线和有交点(s,t)②直线和相交,但是交点未必是(s,t)③直线和平行④直线和必定重合3.下列两个变量之间的关系是相关关系的是④.①正方体的棱长和体积②单位圆中角的度数和所对弧长③单产为常数时,土地面积和总产量④日照时间与水稻的亩产量4.对于回归方程y=4.75x+257,当x=28时,y的估计值为390.5.某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:性别专业非统计专业统计专业男1310女720为了判断主修统计专业是否与性别有关系,根据表中的数据,得到,因为,所以判定主修统计专业与性别有关系,那么这种判断出错的可能性为5%.6.为了研究失重情况下男女飞行员晕飞船的情况,抽取了89名被试者,他们的晕船情况汇总如下表,根据独立性假设检验的方法,不能认为在失重情况下男性比女性更容易晕船(填能或不能)晕机不晕机合计男性233255...