高中数学 第二章 点、直线、平面之间的位置关系 2.2 直线、平面平行的判定及其性质 2.2.4 平面与平面平行的性质课时作业（含解析）新人教A版必修2-新人教A版高一必修2数学试题VIP免费

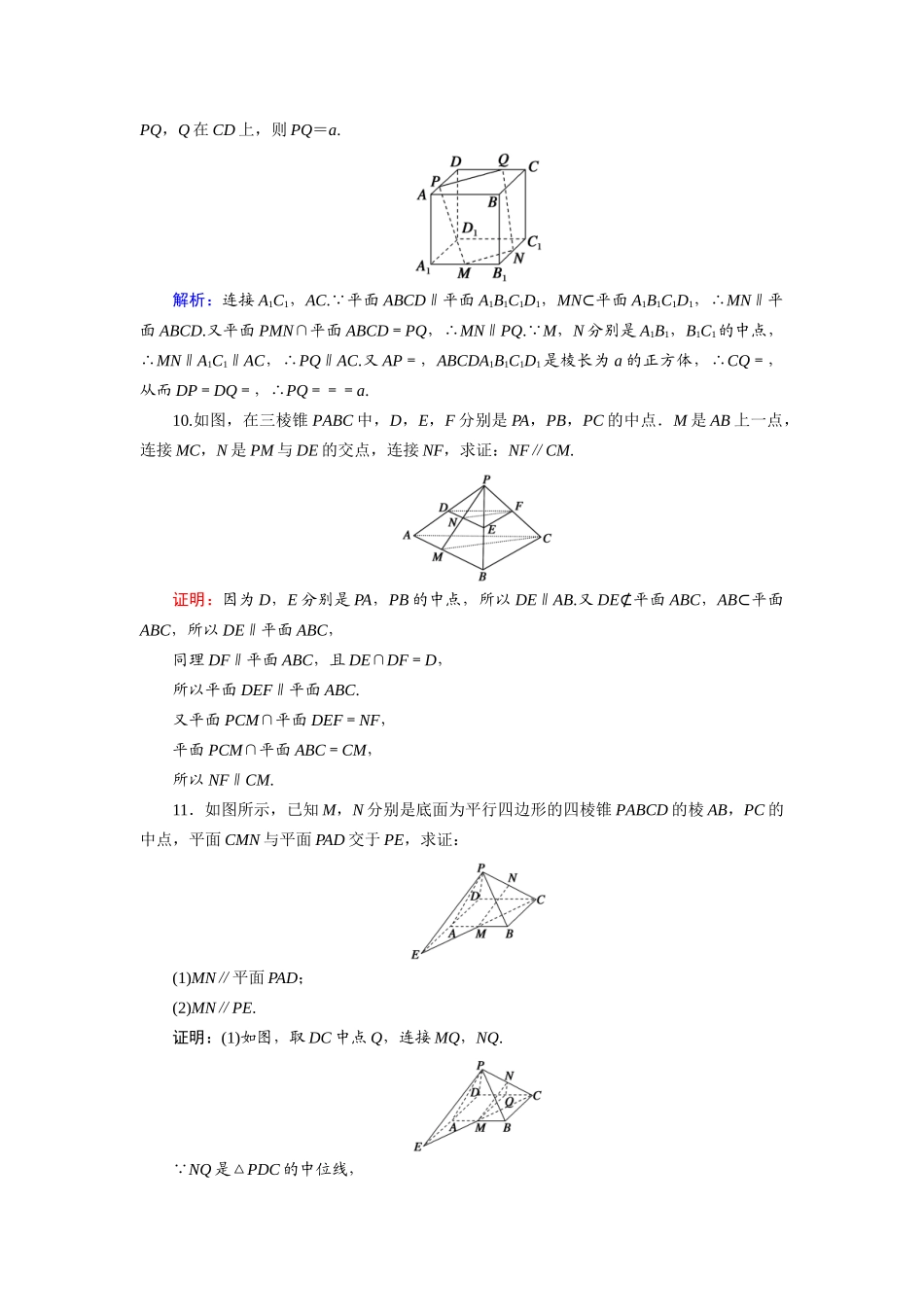
课时作业14平面与平面平行的性质——基础巩固类——1．下列命题中，真命题的个数是(B)①若平面α∥平面β，a⊂α，b⊂β，则a∥b②若平面α∥平面β，a⊂α，b⊂β，则a与b异面③若平面α∥平面β，a⊂α，b⊂β，则a与b一定不相交④若平面α∥平面β，a⊂α，b⊂β，则a与b平行或异面A．1B．2C．3D．4解析：由α∥β，a⊂α，b⊂β知，a与b没有公共点，所以a，b的位置关系为平行或异面，③④正确，故选B.2．如果平面α∥平面β，夹在α和β间的两条线段相等，那么这两条线段所在直线的位置关系是(D)A．平行B．相交C．异面D．平行、相交或异面解析：如图，在正方体ABCDA1B1C1D1中，易知平面ABCD∥平面A1B1C1D1.对于AA1＝BB1，此时AA1∥BB1；对于A1D＝A1B，此时A1D∩A1B＝A1；对于AD1＝A1B，此时AD1与A1B是异面直线．故选D.3．已知长方体ABCDA′B′C′D′，平面α∩平面AC＝EF，平面α∩平面A′C′＝E′F′，则EF与E′F′的位置关系是(A)A．平行B．相交C．异面D．不确定解析：由于平面AC∥平面A′C′，所以EF∥E′F′.4．如图所示，P是三角形ABC所在平面外一点，平面α∥平面ABC，α分别交线段PA，PB，PC于A′，B′，C′，若PA′AA′＝23，则S△A′B′C′S△ABC＝(B)A．225B．425C．25D．45解析：由题意知A′B′∥AB，B′C′∥BC，C′A′∥CA，且PA′AA′＝23，∴＝＝＝.∴S△A′B′C′S△ABC＝425.5.一正方体木块如图所示，点P在平面A′B′C′D′内，经过点P和棱BC将木料锯开，锯开的面必须平整，共有N种锯法，则N为(B)A．0B．1C．2D．无数解析：在平面A′B′C′D′上，过点P作EF∥B′C′，则EF∥BC，所以沿EF，BC所确定的平面锯开即可．由于此平面唯一确定，所以只有一种方法，故选B.6．如图所示，已知正方体ABCDA1B1C1D1的棱长为3，点E在A1B1上，且B1E＝1，记图中阴影平面为平面α，且平面α∥平面BC1E.若平面α∩平面AA1B1B＝A1F，则AF的长为(A)A．1B．1.5C．2D．3解析：因为平面α∥平面BC1E，平面α∩平面AA1B1B＝A1F，平面BC1E∩平面AA1B1B＝BE，所以A1F∥BE.又A1E∥BF，所以四边形A1EBF是平行四边形，所以A1E＝BF＝2，所以AF＝1.7．已知平面α∥平面β，直线a，b分别与平面α，β所成角相等，则直线a，b的位置关系是平行、相交或异面．8．已知平面α∥平面β∥平面γ，两条直线l，m分别与平面α，β，γ相交于点A，B，C和D，E，F，若AB＝6，＝，则AC＝15.解析： α∥β∥γ，∴＝.由＝，得＝，∴＝.而AB＝6，∴BC＝9，∴AC＝AB＋BC＝15.9.如图所示，ABCDA1B1C1D1是棱长为a的正方体，M，N分别是下底面的棱A1B1，B1C1的中点，P是上底面的棱AD上的一点，AP＝，过P，M，N的平面交上底面于PQ，Q在CD上，则PQ＝a.解析：连接A1C1，AC. 平面ABCD∥平面A1B1C1D1，MN⊂平面A1B1C1D1，∴MN∥平面ABCD.又平面PMN∩平面ABCD＝PQ，∴MN∥PQ. M，N分别是A1B1，B1C1的中点，∴MN∥A1C1∥AC，∴PQ∥AC.又AP＝，ABCDA1B1C1D1是棱长为a的正方体，∴CQ＝，从而DP＝DQ＝，∴PQ＝＝＝a.10.如图，在三棱锥PABC中，D，E，F分别是PA，PB，PC的中点．M是AB上一点，连接MC，N是PM与DE的交点，连接NF，求证：NF∥CM.证明：因为D，E分别是PA，PB的中点，所以DE∥AB.又DE⊄平面ABC，AB⊂平面ABC，所以DE∥平面ABC，同理DF∥平面ABC，且DE∩DF＝D，所以平面DEF∥平面ABC.又平面PCM∩平面DEF＝NF，平面PCM∩平面ABC＝CM，所以NF∥CM.11．如图所示，已知M，N分别是底面为平行四边形的四棱锥PABCD的棱AB，PC的中点，平面CMN与平面PAD交于PE，求证：(1)MN∥平面PAD；(2)MN∥PE.证明：(1)如图，取DC中点Q，连接MQ，NQ. NQ是△PDC的中位线，∴NQ∥PD. NQ⊄平面PAD，PD⊂平面PAD，∴NQ∥平面PAD. M，Q分别是AB，DC的中点，且四边形ABCD是平行四边形，∴MQ∥AD. MQ⊄平面PAD，AD⊂平面PAD，∴MQ∥平面PAD. MQ∩NQ＝Q，∴平面MNQ∥平面PAD. MN⊂平面MNQ，∴MN∥平面PAD.(2) 平面MNQ∥平面PAD，平面PEC∩平面MNQ＝MN，平面PEC∩平面PAD＝PE.∴MN∥PE.——能力提升类——12．平面α截一个三棱锥，如果截面是梯形，那么平面α必定和这个三棱锥的(C)A．一个侧面平行B．底面平行C．仅一条...