课时作业64几何概型一、选择题1.某市地铁2号线到站的时间间隔为5分钟,某人在地铁2号线站台等待时间超过4分钟的概率为p1,2路车到站的时间相隔为8分钟,某人在2路车站牌处等待时间超过6分钟的概率为p2,则p1与p2的大小关系为()A.p1=p2B.p1>p2C.p1
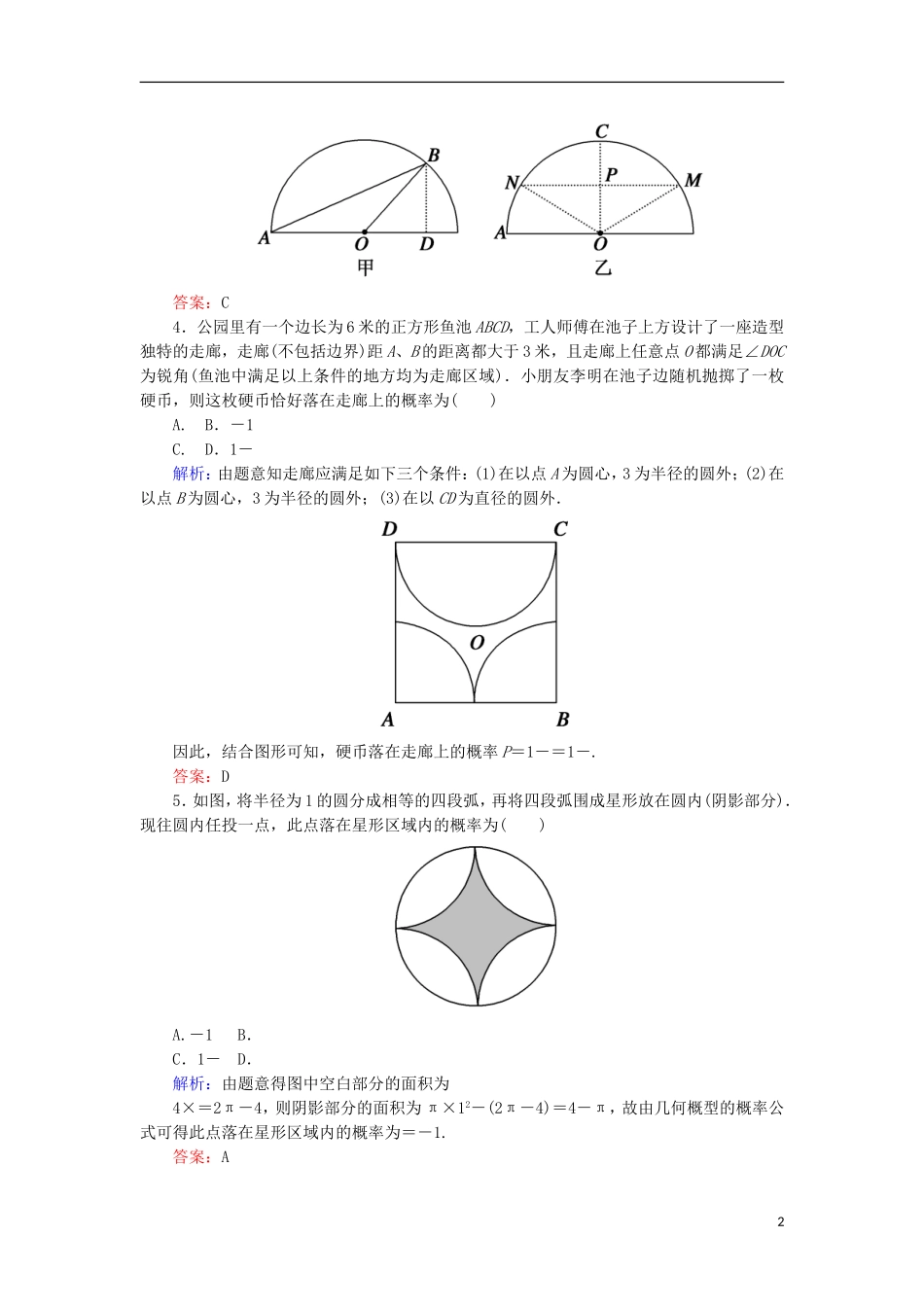
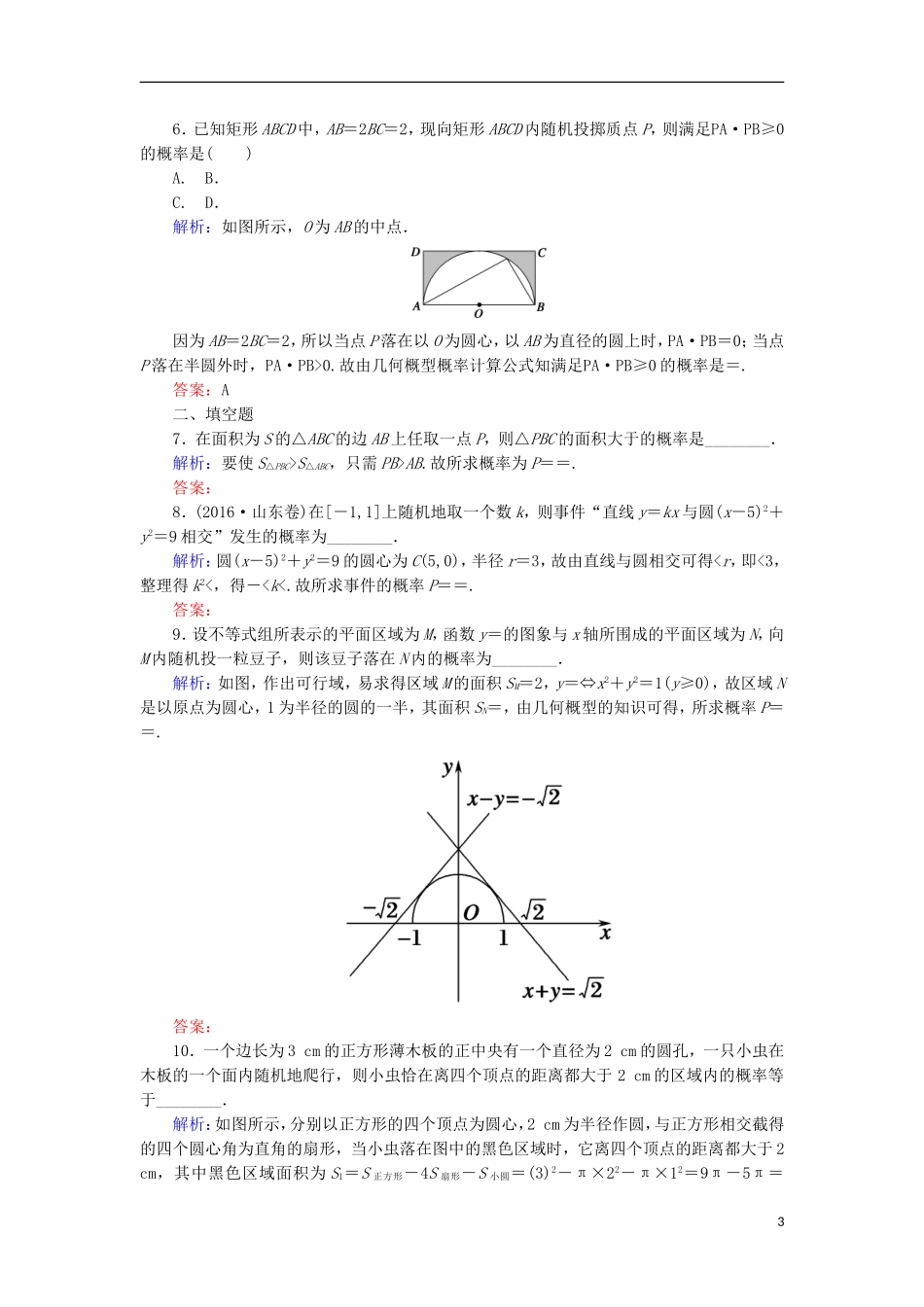
,即|BD|>.如图乙所示,作CO⊥OA,取P为CO的中点,过P作MN⊥OC,连接OM,ON,则当点B在上运动(不包括点M,N)时,|BD|>,故所求概率P==.故选C.1答案:C4.公园里有一个边长为6米的正方形鱼池ABCD,工人师傅在池子上方设计了一座造型独特的走廊,走廊(不包括边界)距A、B的距离都大于3米,且走廊上任意点O都满足∠DOC为锐角(鱼池中满足以上条件的地方均为走廊区域).小朋友李明在池子边随机抛掷了一枚硬币,则这枚硬币恰好落在走廊上的概率为()A.B.-1C.D.1-解析:由题意知走廊应满足如下三个条件:(1)在以点A为圆心,3为半径的圆外;(2)在以点B为圆心,3为半径的圆外;(3)在以CD为直径的圆外.因此,结合图形可知,硬币落在走廊上的概率P=1-=1-.答案:D5.如图,将半径为1的圆分成相等的四段弧,再将四段弧围成星形放在圆内(阴影部分).现往圆内任投一点,此点落在星形区域内的概率为()A.-1B.C.1-D.解析:由题意得图中空白部分的面积为4×=2π-4,则阴影部分的面积为π×12-(2π-4)=4-π,故由几何概型的概率公式可得此点落在星形区域内的概率为=-1.答案:A26.已知矩形ABCD中,AB=2BC=2,现向矩形ABCD内随机投掷质点P,则满足PA·PB≥0的概率是()A.B.C.D.解析:如图所示,O为AB的中点.因为AB=2BC=2,所以当点P落在以O为圆心,以AB为直径的圆上时,PA·PB=0;当点P落在半圆外时,PA·PB>0.故由几何概型概率计算公式知满足PA·PB≥0的概率是=.答案:A二、填空题7.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是________.解析:要使S△PBC>S△ABC,只需PB>AB.故所求概率为P==.答案:8.(2016·山东卷)在[-1,1]上随机地取一个数k,则事件“直线y=kx与圆(x-5)2+y2=9相交”发生的概率为________.解析:圆(x-5)2+y2=9的圆心为C(5,0),半径r=3,故由直线与圆相交可得