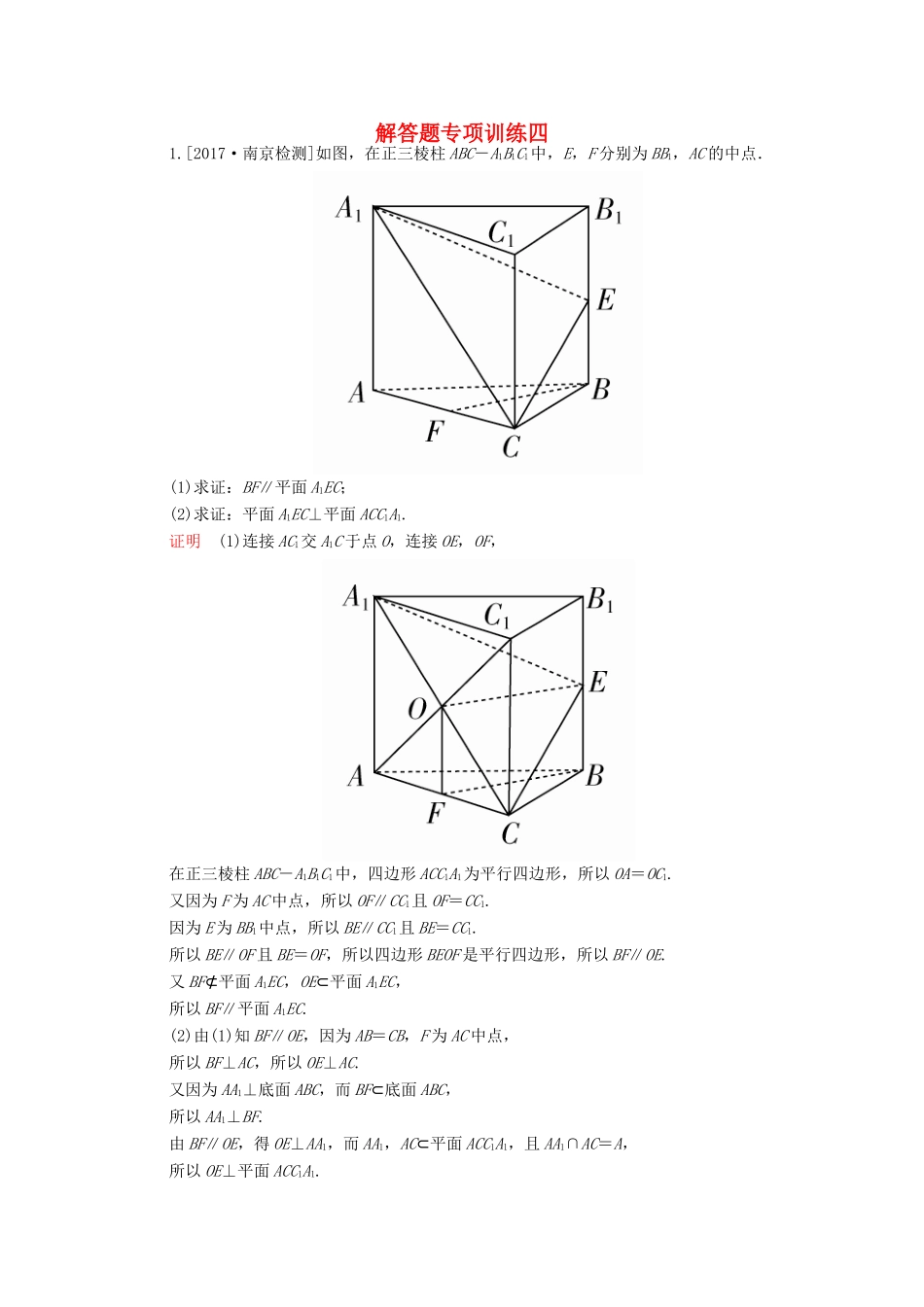
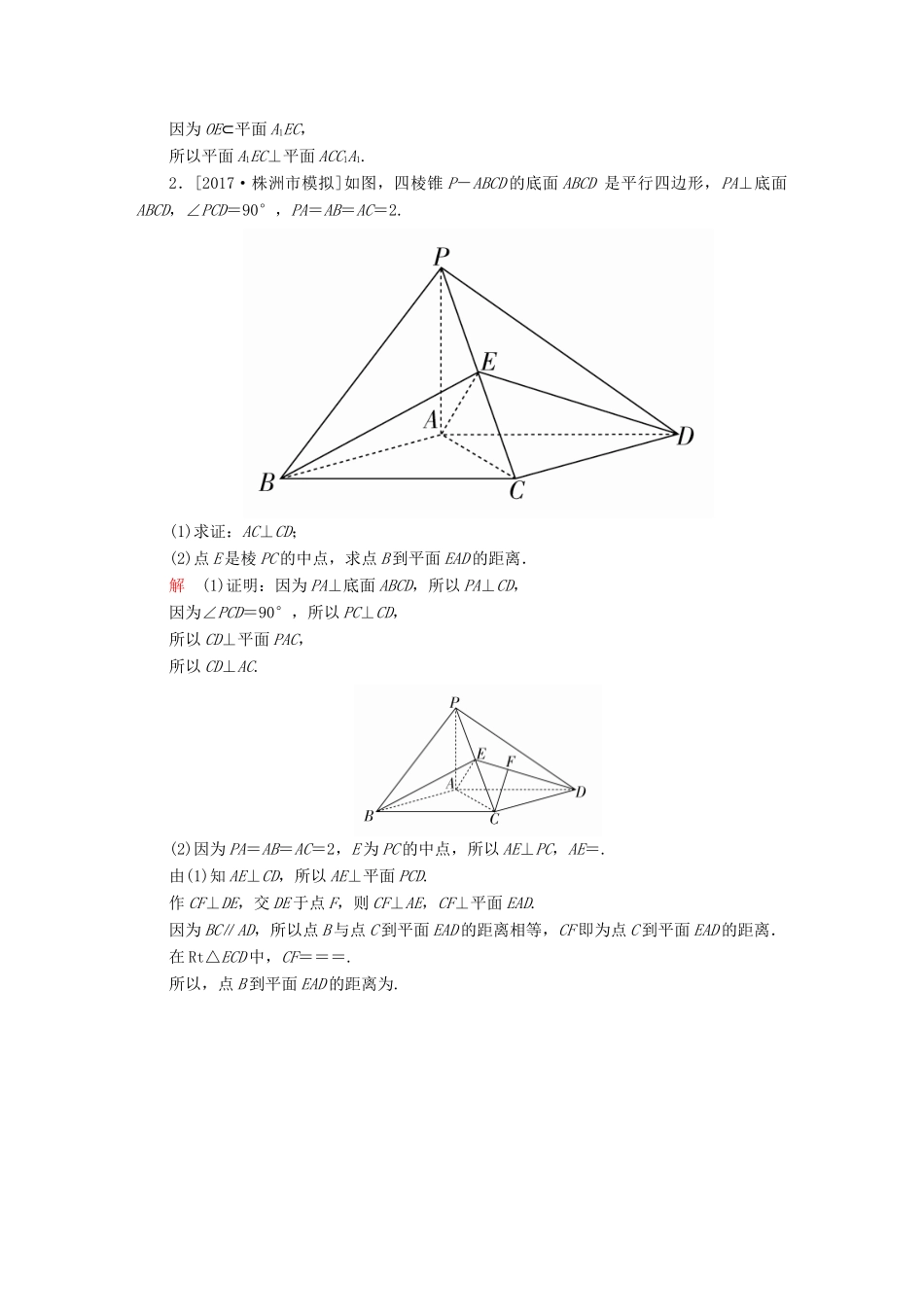
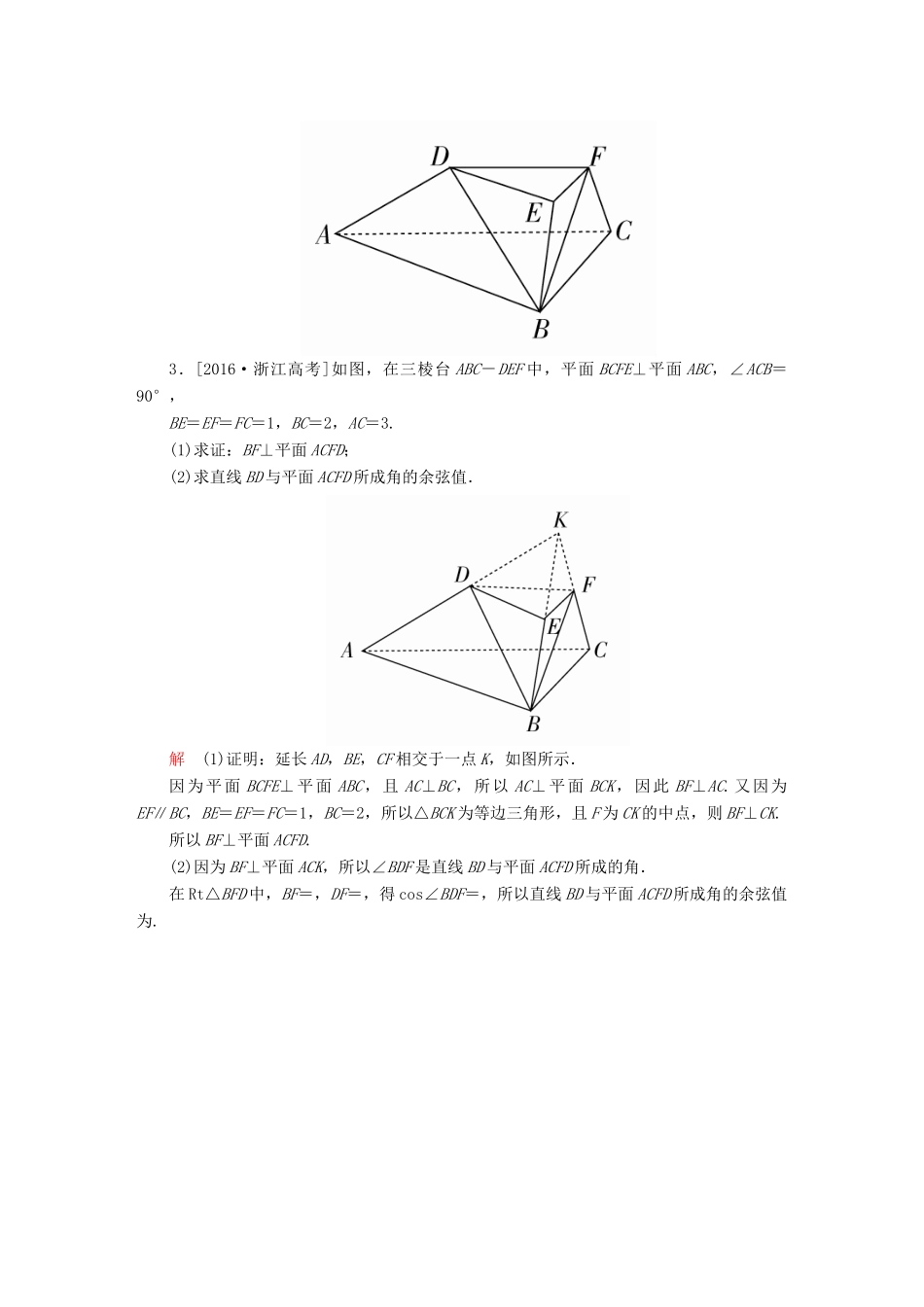
解答题专项训练四1.[2017·南京检测]如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.(1)求证:BF∥平面A1EC;(2)求证:平面A1EC⊥平面ACC1A1.证明(1)连接AC1交A1C于点O,连接OE,OF,在正三棱柱ABC-A1B1C1中,四边形ACC1A1为平行四边形,所以OA=OC1.又因为F为AC中点,所以OF∥CC1且OF=CC1.因为E为BB1中点,所以BE∥CC1且BE=CC1.所以BE∥OF且BE=OF,所以四边形BEOF是平行四边形,所以BF∥OE.又BF⊄平面A1EC,OE⊂平面A1EC,所以BF∥平面A1EC.(2)由(1)知BF∥OE,因为AB=CB,F为AC中点,所以BF⊥AC,所以OE⊥AC.又因为AA1⊥底面ABC,而BF⊂底面ABC,所以AA1⊥BF.由BF∥OE,得OE⊥AA1,而AA1,AC⊂平面ACC1A1,且AA1∩AC=A,所以OE⊥平面ACC1A1.因为OE⊂平面A1EC,所以平面A1EC⊥平面ACC1A1.2.[2017·株洲市模拟]如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC=2.(1)求证:AC⊥CD;(2)点E是棱PC的中点,求点B到平面EAD的距离.解(1)证明:因为PA⊥底面ABCD,所以PA⊥CD,因为∠PCD=90°,所以PC⊥CD,所以CD⊥平面PAC,所以CD⊥AC.(2)因为PA=AB=AC=2,E为PC的中点,所以AE⊥PC,AE=.由(1)知AE⊥CD,所以AE⊥平面PCD.作CF⊥DE,交DE于点F,则CF⊥AE,CF⊥平面EAD.因为BC∥AD,所以点B与点C到平面EAD的距离相等,CF即为点C到平面EAD的距离.在Rt△ECD中,CF===.所以,点B到平面EAD的距离为.3.[2016·浙江高考]如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.(1)求证:BF⊥平面ACFD;(2)求直线BD与平面ACFD所成角的余弦值.解(1)证明:延长AD,BE,CF相交于一点K,如图所示.因为平面BCFE⊥平面ABC,且AC⊥BC,所以AC⊥平面BCK,因此BF⊥AC.又因为EF∥BC,BE=EF=FC=1,BC=2,所以△BCK为等边三角形,且F为CK的中点,则BF⊥CK.所以BF⊥平面ACFD.(2)因为BF⊥平面ACK,所以∠BDF是直线BD与平面ACFD所成的角.在Rt△BFD中,BF=,DF=,得cos∠BDF=,所以直线BD与平面ACFD所成角的余弦值为.4.[2017·抚州市模拟]如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=30°,PD⊥平面ABCD,AD=2,点E为AB上一点,且=m,点F为PD的中点.(1)若m=,证明:直线AF∥平面PEC;(2)是否存在一个常数m,使得平面PED⊥平面PAB?若存在,求出m的值;若不存在,请说明理由.解(1)证明:作FM∥CD交PC于点M,连接ME. 点F为PD的中点,∴FM=CD. m=,∴AE=AB=FM,又FM∥CD∥AE,∴四边形AEMF为平行四边形,∴AF∥EM. AF⊄平面PEC,EM⊂平面PEC,∴直线AF∥平面PEC.(2)存在常数m=,使得平面PED⊥平面PAB.要使平面PED⊥平面PAB,只需AB⊥DE.此时AB=AD=2,∠DAB=30°,∴AE=ADcos30°=.又 PD⊥平面ABCD,∴PD⊥AB. PD∩DE=D,∴AB⊥平面PDE. AB⊂平面PAB,∴平面PDE⊥平面PAB,因此m==.5.[2015·陕西高考]如图1,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图2中△A1BE的位置,得到四棱锥A1-BCDE.(1)证明:CD⊥平面A1OC;(2)当平面A1BE⊥平面BCDE时,四棱锥A1-BCDE的体积为36,求a的值.解(1)证明:在图1中,因为AB=BC=AD=a,E是AD的中点,∠BAD=,所以BE⊥AC,即在图2中,BE⊥A1O,BE⊥OC,从而BE⊥平面A1OC,又CD∥BE,所以CD⊥平面A1OC.(2)由已知,平面A1BE⊥平面BCDE,且平面A1BE∩平面BCDE=BE,又由(1),A1O⊥BE,所以A1O⊥平面BCDE,即A1O是四棱锥A1-BCDE的高.由图1知,A1O=AB=a,平行四边形BCDE的面积S=BC·AB=a2.从而四棱锥A1-BCDE的体积为V=S·A1O=×a2×a=a3,由a3=36,得a=6.6.如图,三棱柱ABC-A1B1C1中,平面AA1B1B⊥平面ABC,D是AC的中点.(1)求证:B1C∥平面A1BD;(2)若∠A1AB=∠ACB=60°,AB=BB1,AC=2,BC=1,求三棱锥A1-ABD的体积.解(1)证明:连接AB1交A1B于点O,则O为AB1的中点,连接DO. D是AC的中点,∴DO为△ACB1的中位线,∴OD∥B1C.又OD⊂平面A1BD,B1C⊄平面A1BD,∴B1C∥平面A1BD.(2) AC=2,BC=1,∠ACB=60°,∴AB2=AC2+BC2-2AC·BC·cos∠ACB=3,...