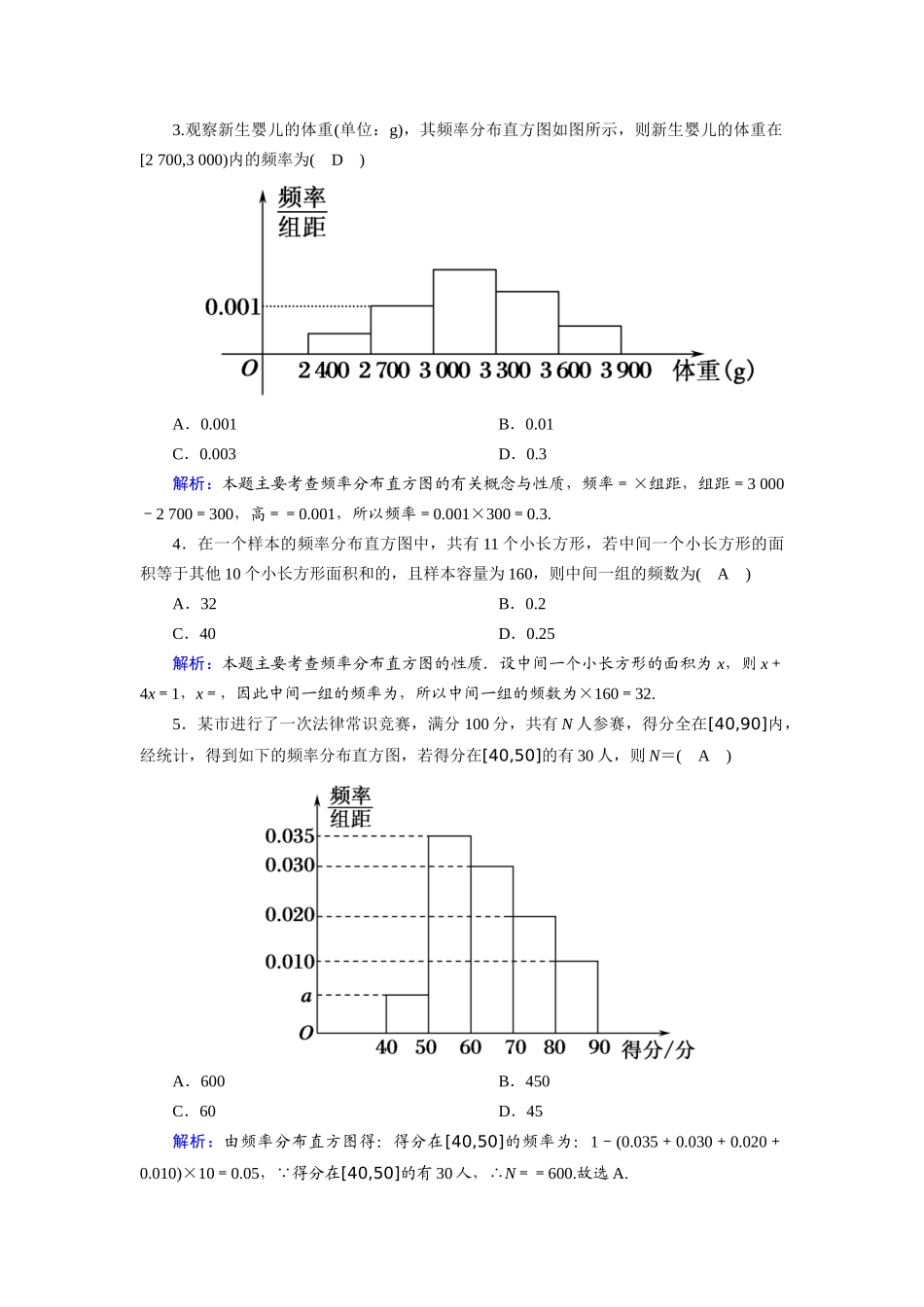
课时作业13用样本的频率分布估计总体分布——基础巩固类——1.一个容量为n的样本,已知某组的频率为0.25,频数为5,则n=(C)A.50B.40C.20D.10解析: 频率=,∴0.25=,n=20.2.如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的频率为(B)A.0.2B.0.4C.0.5D.0.6解析:由茎叶图知落在区间[22,30)内的数据有22,22,27,29,共4个,因为共有10个数据,所以数据落在区间[22,30)内的频率为=0.4.3.观察新生婴儿的体重(单位:g),其频率分布直方图如图所示,则新生婴儿的体重在[2700,3000)内的频率为(D)A.0.001B.0.01C.0.003D.0.3解析:本题主要考查频率分布直方图的有关概念与性质,频率=×组距,组距=3000-2700=300,高==0.001,所以频率=0.001×300=0.3.4.在一个样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形面积和的,且样本容量为160,则中间一组的频数为(A)A.32B.0.2C.40D.0.25解析:本题主要考查频率分布直方图的性质.设中间一个小长方形的面积为x,则x+4x=1,x=,因此中间一组的频率为,所以中间一组的频数为×160=32.5.某市进行了一次法律常识竞赛,满分100分,共有N人参赛,得分全在[40,90]内,经统计,得到如下的频率分布直方图,若得分在[40,50]的有30人,则N=(A)A.600B.450C.60D.45解析:由频率分布直方图得:得分在[40,50]的频率为:1-(0.035+0.030+0.020+0.010)×10=0.05, 得分在[40,50]的有30人,∴N==600.故选A.6.下列关于样本频率分布折线图与总体密度曲线的关系的说法中,正确的是(D)A.频率分布折线图与总体密度曲线无关B.频率分布折线图就是总体密度曲线C.样本容量很大的频率分布折线图就是总体密度曲线D.如果样本容量无限增大,分组的组距无限减小,那么频率分布折线图就会无限接近于总体密度曲线解析:选项正误理由A×当总体个数较多时,随着样本容量的增加,组数增加,组距减小,频率分布折线图趋向于总体密度曲线,所以两者有关B×只有当样本容量很大时,频率分布折线图趋向于总体密度曲线C×总体密度曲线是由频率分布折线图估计的,样本容量越大就越准确D√频率分布折线图在样本容量无限增大,分组的组距无限减小的情况下会无限接近于一条光滑曲线,这条光滑曲线就是总体密度曲线7.一个频数分布表(样本容量为30)不小心被损坏了一部分,若样本中数据在[20,60)上的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数共为(A)A.15B.16C.17D.19解析:由题意得样本在[40,50),[50,60)内的数据个数共为30×0.8-4-5=15.8.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为(B)A.588B.480C.450D.120解析: 少于60分的学生人数为600×(0.05+0.15)=120,∴不少于60分的学生人数为480.9.为了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高,单位:cm)分组情况如下:分组151.5~158.5158.5~165.5165.5~172.5172.5~179.5频数621m频率a0.1则表中的m=6,a=0.45.解析:由频率的计算公式得0.1=,m=6,所以落在165.5~172.5的男生的频数为60-(6+21+6)=27,所以a==0.45.10.如图是将高三某班60名学生参加某次数学模拟考试所得的成绩(成绩均为整数)整理后画出的频率分布直方图,则此班的优秀(120分及以上为优秀)率为30%.解析:由频率分布直方图知数据落在120~150的频率为10×(0.0225+0.005+0.0025)=0.3=30%,即优秀率为30%.11.在样本的频率分布直方图中,一共有m(m≥3)个小矩形,第3个小矩形的面积等于其余m-1个小矩形面积和的,且样本容量为100,则第3组的频数是20.解析:由s=(1-s),解得s=0.2,∴100×0.2=20.12.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(单位:分):[40,50),[50,60),…,[90,100],然后画出如图所示...