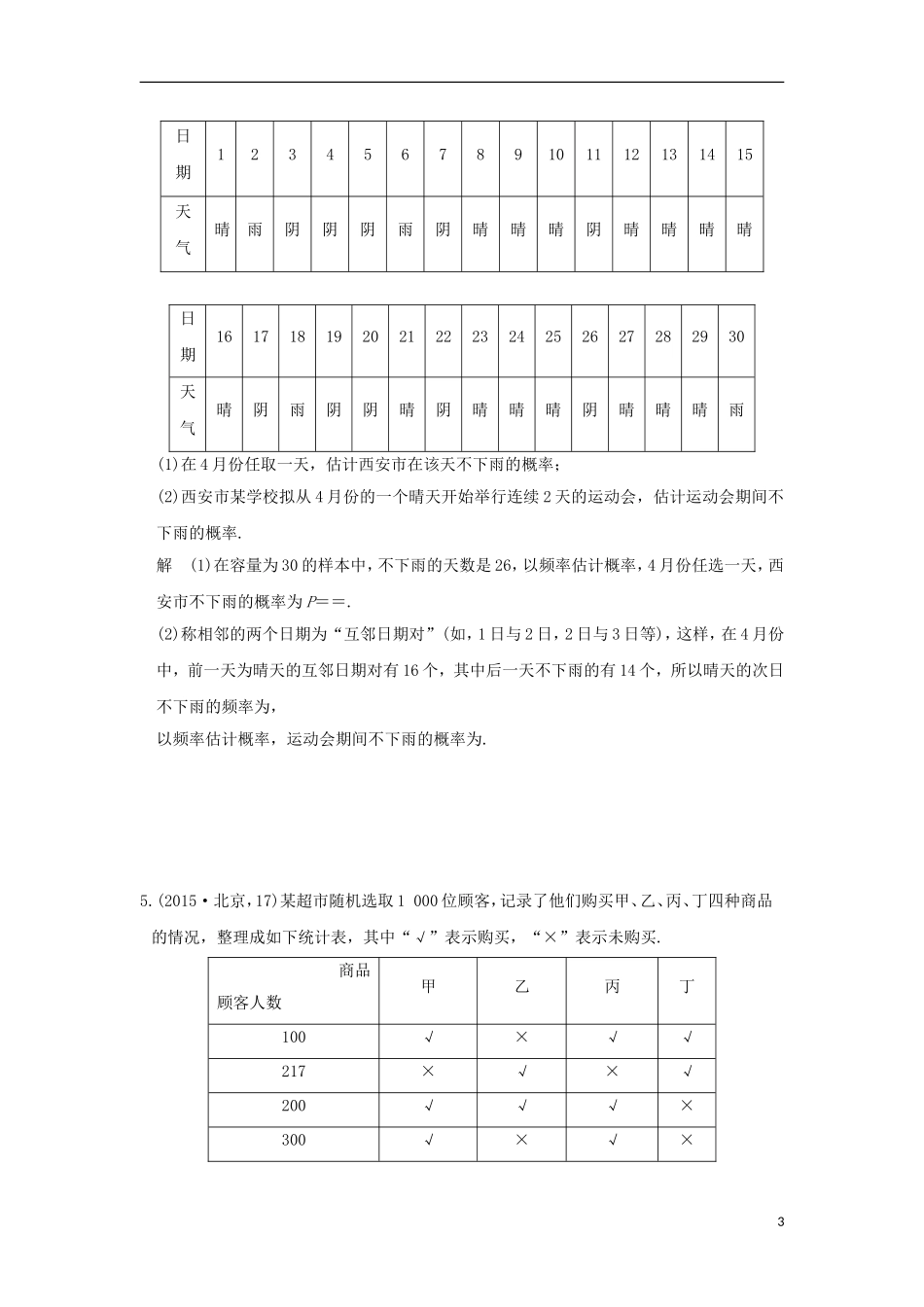
【大高考】2017版高考数学一轮总复习第10章概率与统计第一节随机事件及其概率AB卷文新人教A版1.(2013·新课标全国Ⅰ,3)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是()A.B.C.D.解析4个取2个有6种方法,差为2的只有1和3,2和4.故P==.答案B2.(2016·新课标全国Ⅱ,18)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:上年度出险次数01234≥5保费0.85aa1.25a1.5a1.75a2a随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:出险次数01234≥5频数605030302010(1)记A为事件:“一续保人本年度的保费不高于基本保费”.求P(A)的估计值;(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;(3)求续保人本年度的平均保费的估计值.解(1)事件A发生当且仅当一年内出险次数小于2,由所给数据知,一年内出险次数小于2的频率为=0.55,故P(A)的估计值为0.55.(2)事件B发生当且仅当一年内出险次数大于1且小于4,由所给数据知,一年内出险次数大于1且小于4的频率为=0.3,故P(B)的估计值为0.3.(3)由所给数据得保费0.85aa1.25a1.5a1.75a2a频率0.300.250.150.150.100.051调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.1925a.因此,续保人本年度平均保费的估计值为1.1925a.1.(2015·广东,7)已知5件产品中有2件次品,其余为合格品.现从这5件产品中任取2件,恰有一件次品的概率为()A.0.4B.0.6C.0.8D.1解析5件产品中有2件次品,记为a,b,有3件合格品,记为c,d,e,从这5件产品中任取2件,结果有(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e)共10种.恰有一件次品的结果有6种,则其概率为p==0.6.答案B2.(2015·江苏,5)袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为________.解析这两只球颜色相同的概率为,故两只球颜色不同的概率为1-=.答案3.(2015·湖南,16)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖方法是:从装有2个红球A1,A2和1个白球B的甲箱与装有2个红球a1,a2和2个白球b1、b2的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖.(1)用球的标号列出所有可能的摸出结果;(2)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由.解(1)所有可能结果为:(A1,a1),(A1,a2),(A1,b1),(A1,b2),(A2,a1),(A2,a2),(A2,b1),(A2,b2);(B,a1),(B,a2),(B,b1),(B,b2)共计12种结果.(2)不正确,理由如下:设“中奖”为事件A,则P(A)==,P(A)=1-=,P(A)<P(A),故此种说法不正确.4.(2015·陕西,19)随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:2日期123456789101112131415天气晴雨阴阴阴雨阴晴晴晴阴晴晴晴晴日期161718192021222324252627282930天气晴阴雨阴阴晴阴晴晴晴阴晴晴晴雨(1)在4月份任取一天,估计西安市在该天不下雨的概率;(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.解(1)在容量为30的样本中,不下雨的天数是26,以频率估计概率,4月份任选一天,西安市不下雨的概率为P==.(2)称相邻的两个日期为“互邻日期对”(如,1日与2日,2日与3日等),这样,在4月份中,前一天为晴天的互邻日期对有16个,其中后一天不下雨的有14个,所以晴天的次日不下雨的频率为,以频率估计概率,运动会期间不下雨的概率为.5.(2015·北京,17)某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.商品顾客人数甲乙丙丁100√×√√217×√×√200√√√×300√×√×385√×××98×√××(1)估计顾客同时购买乙和丙的概率;(2)估计顾客在甲、乙、丙、丁中同时购买3种商品的概率;(3)如果顾客购买了甲,则该顾客同时购买乙、...