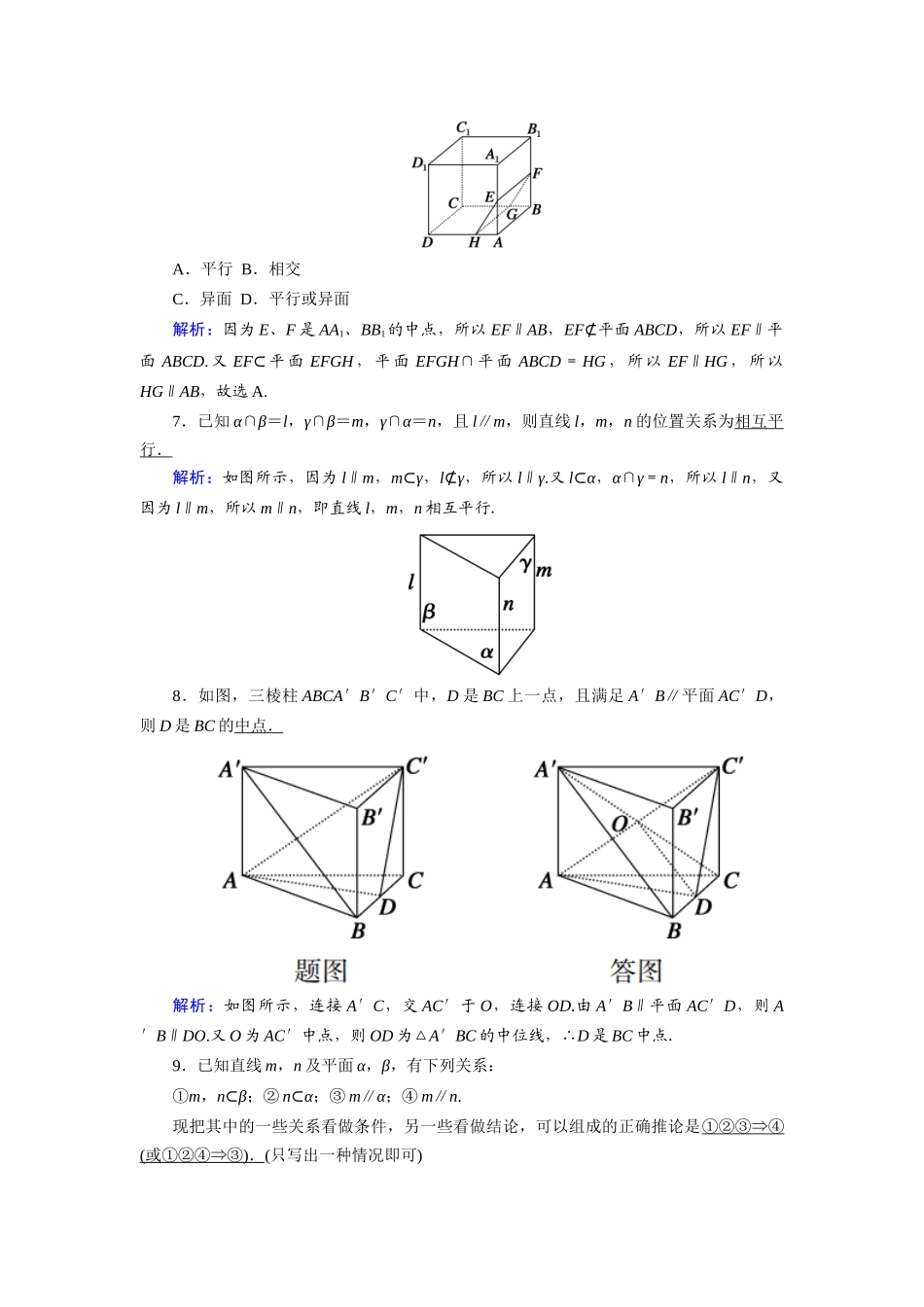
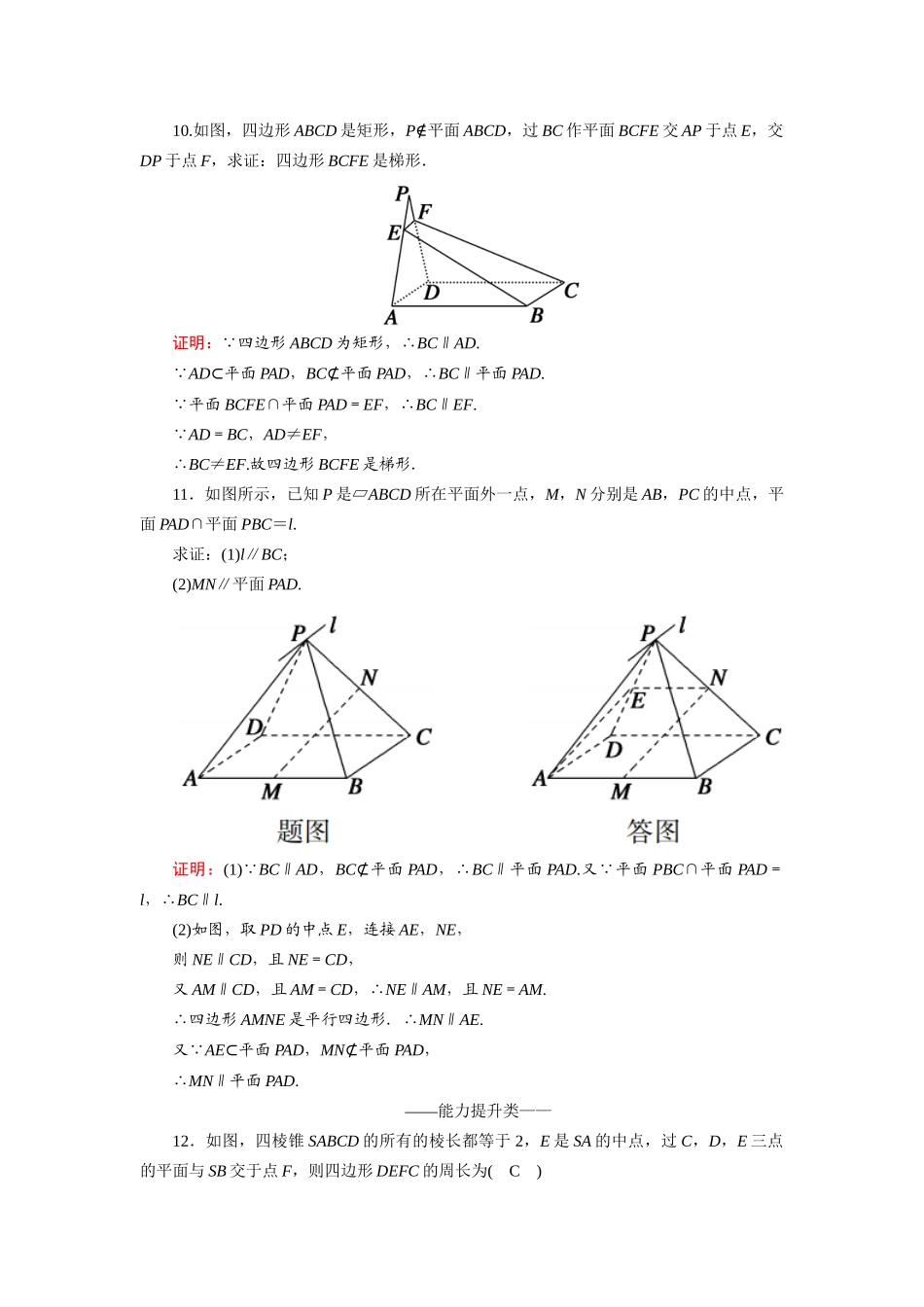
课时作业13直线与平面平行的性质——基础巩固类——1.若直线a不平行于平面α,则下列结论成立的是(D)A.α内的所有直线都与直线a异面B.α内不存在与a平行的直线C.α内的直线都与a相交D.直线a与平面α有公共点解析:a不平行于α,则a与α相交或a在α内,故A,B,C不正确,故选D.2.下列说法正确的是(D)A.若直线a∥平面α,直线b∥平面α,则直线a∥直线bB.若直线a∥平面α,直线a与直线b相交,则直线b与平面α相交C.若直线a∥平面α,直线a∥直线b,则直线b∥平面αD.若直线a∥平面α,则直线a与平面α内的任意一条直线都无公共点解析:A中,直线a与直线b也可能异面、相交,所以不正确;B中,直线b也可能与平面α平行,所以不正确;C中,直线b也可能在平面α内,所以不正确;根据直线与平面平行的定义可知D正确.3.已知直线a∥平面α,P∈α,那么过点P且平行于a的直线(C)A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,且在平面α内D.有无数条,一定在平面α内解析:根据线面平行的性质定理可知C正确.4.设a,b是两条直线,α,β是两个平面,若a∥α,a⊂β,α∩β=b,则α内与b相交的直线与a的位置关系是(C)A.平行B.相交C.异面D.平行或异面解析:条件即为线面平行的性质定理,所以a∥b,又a与α无公共点,故选C.5.与两个相交平面的交线平行的直线和这两个平面的位置关系是(D)A.都平行B.都相交C.在两个平面内D.至少和其中一个平行解析:它可以在一个平面内与另一个平面平行,也可以和两个平面都平行.6.如图所示,长方体ABCDA1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG和AB的位置关系是(A)A.平行B.相交C.异面D.平行或异面解析:因为E、F是AA1、BB1的中点,所以EF∥AB,EF⊄平面ABCD,所以EF∥平面ABCD.又EF⊂平面EFGH,平面EFGH∩平面ABCD=HG,所以EF∥HG,所以HG∥AB,故选A.7.已知α∩β=l,γ∩β=m,γ∩α=n,且l∥m,则直线l,m,n的位置关系为相互平行.解析:如图所示,因为l∥m,m⊂γ,l⊄γ,所以l∥γ.又l⊂α,α∩γ=n,所以l∥n,又因为l∥m,所以m∥n,即直线l,m,n相互平行.8.如图,三棱柱ABCA′B′C′中,D是BC上一点,且满足A′B∥平面AC′D,则D是BC的中点.解析:如图所示,连接A′C,交AC′于O,连接OD.由A′B∥平面AC′D,则A′B∥DO.又O为AC′中点,则OD为△A′BC的中位线,∴D是BC中点.9.已知直线m,n及平面α,β,有下列关系:①m,n⊂β;②n⊂α;③m∥α;④m∥n.现把其中的一些关系看做条件,另一些看做结论,可以组成的正确推论是①②③⇒④(或①②④⇒③).(只写出一种情况即可)10.如图,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE是梯形.证明: 四边形ABCD为矩形,∴BC∥AD. AD⊂平面PAD,BC⊄平面PAD,∴BC∥平面PAD. 平面BCFE∩平面PAD=EF,∴BC∥EF. AD=BC,AD≠EF,∴BC≠EF.故四边形BCFE是梯形.11.如图所示,已知P是▱ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.求证:(1)l∥BC;(2)MN∥平面PAD.证明:(1) BC∥AD,BC⊄平面PAD,∴BC∥平面PAD.又 平面PBC∩平面PAD=l,∴BC∥l.(2)如图,取PD的中点E,连接AE,NE,则NE∥CD,且NE=CD,又AM∥CD,且AM=CD,∴NE∥AM,且NE=AM.∴四边形AMNE是平行四边形.∴MN∥AE.又 AE⊂平面PAD,MN⊄平面PAD,∴MN∥平面PAD.——能力提升类——12.如图,四棱锥SABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为(C)A.2+B.3+C.3+2D.2+2解析:因为CD∥AB,AB⊂平面SAB,CD⊄平面SAB,所以CD∥平面SAB.又CD⊂平面CDEF,平面SAB∩平面CDEF=EF,所以CD∥EF,所以四边形CDEF为等腰梯形,且CD=2,EF=1,DE=CF=,所以四边形CDEF的周长为3+2,选C.13.如图,已知正方体AC1的棱长为1,点P是平面A1ADD1的中心,点Q是平面A1B1C1D1的对角线B1D1上一点,且PQ∥平面AA1B1B,则线段PQ的长为.解析:当Q是平面A1B1C1D1的中心时,PQ∥C1D∥AB1,满足条件PQ∥平面AA1B1B....