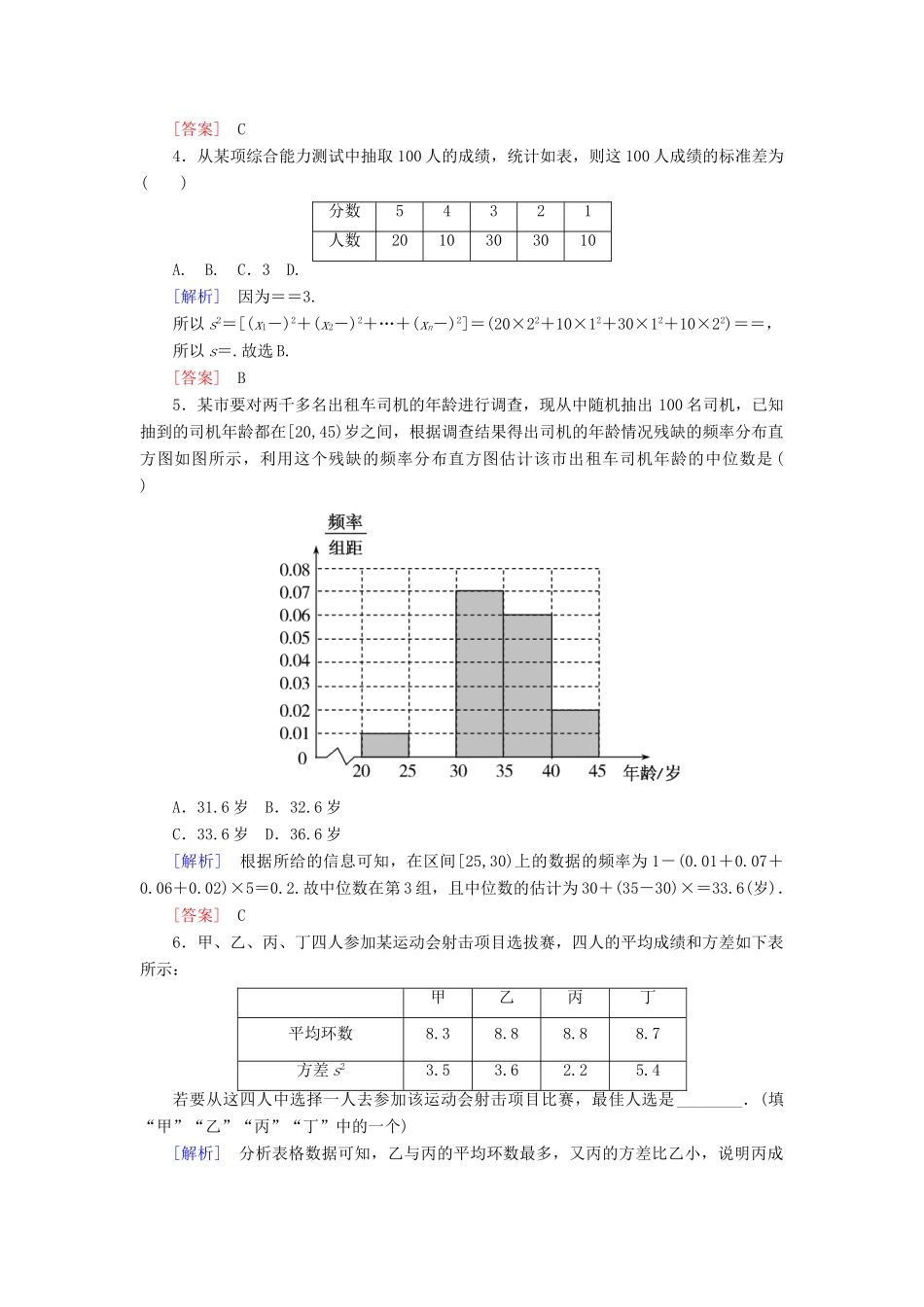
课后作业(十四)(时间45分钟)学业水平合格练(时间25分钟)1.为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是()A.x1,x2,…,xn的平均数B.x1,x2,…,xn的标准差C.x1,x2,…,xn的最大值D.x1,x2,…,xn的中位数[解析]标准差衡量样本的稳定程度,故选B.[答案]B2.如图,茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为()A.2,6B.2,7C.3,6D.3,7[解析]由题可知=17,所以x=3,由乙组数据的中位数为17可得y=7,选D.[答案]D3.为了了解某同学的数学学习情况,对他的6次数学测试成绩进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是()A.中位数为83B.众数为85C.平均数为85D.方差为19[解析]由茎叶图可知,该同学的6次数学测试成绩分别是78,83,83,85,91,90,由这些数据可求得该同学数学成绩的众数为83,中位数为84,平均数为==85,方差为s2=[(78-85)2+(83-85)2+(83-85)2+(85-85)2+(91-85)2+(90-85)2]≈19.7,故选C.[答案]C4.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为()分数54321人数2010303010A.B.C.3D.[解析]因为==3.所以s2=[(x1-)2+(x2-)2+…+(xn-)2]=(20×22+10×12+30×12+10×22)==,所以s=.故选B.[答案]B5.某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数是()A.31.6岁B.32.6岁C.33.6岁D.36.6岁[解析]根据所给的信息可知,在区间[25,30)上的数据的频率为1-(0.01+0.07+0.06+0.02)×5=0.2.故中位数在第3组,且中位数的估计为30+(35-30)×=33.6(岁).[答案]C6.甲、乙、丙、丁四人参加某运动会射击项目选拔赛,四人的平均成绩和方差如下表所示:甲乙丙丁平均环数8.38.88.88.7方差s23.53.62.25.4若要从这四人中选择一人去参加该运动会射击项目比赛,最佳人选是________.(填“甲”“乙”“丙”“丁”中的一个)[解析]分析表格数据可知,乙与丙的平均环数最多,又丙的方差比乙小,说明丙成绩发挥得较为稳定,所以最佳人选为丙.[答案]丙7.若a1,a2,…,a20,这20个数据的平均数为,方差为0.20,则数据a1,a2,…,a20,这21个数据的方差约为________.[解析]这21个数的平均数仍为,从而方差为×[20×0.2+(-)2]≈0.19.[答案]0.198.已知样本9,10,11,x,y的平均数是10,标准差是,则xy=________.[解析]由平均数是10,得x+y=20,由标准差是,得=,所以(x-10)2+(y-10)2=8,所以xy=96.[答案]969.甲、乙两种冬小麦实验品种连续5年的平均单位面积产量如下(单位:t/km2):第1年第2年第3年第4年第5年甲9.89.910.11010.2乙9.410.310.89.79.8若某村要从中引进一种冬小麦大量种植,给出你的建议.[解]由题意得甲=乙=10.s=×[(9.8-10)2+(9.9-10)2+(10.1-10)2+(10-10)2+(10.2-10)2]=0.02,s=×[(9.4-10)2+(10.3-10)2+(10.8-10)2+(9.7-10)2+(9.8-10)2]=0.244,甲、乙两种冬小麦的平均产量都等于10,且s