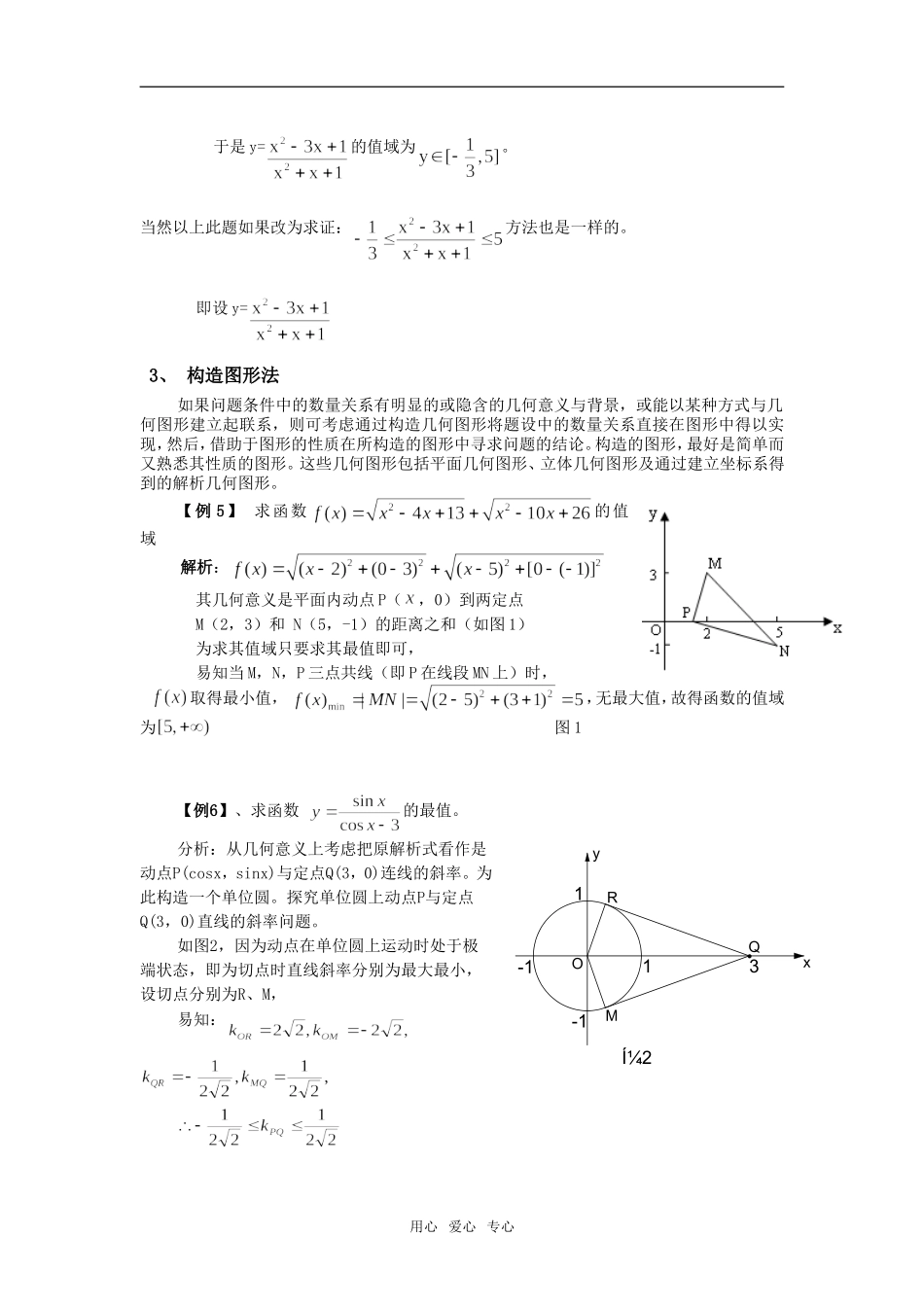
高中数学思想方法专题(五)---构造的思想方法所谓构造的思想方法,就是指在对问题进行透彻地分析,对其实质进行深刻地了解的基础上,借助于逻辑分析或长期积累的经验,发挥高度的想象和创造性,将原来的问题从原来的模式转化为更能反映其本质特征的新模式的思想方法。构造思想是一种很活跃的创造性思想方法,它能沟通数学各个不同的分支,甚至还能沟通数学与其他的学科,实现跨度极大的问题转化,这是一种难度大、规律不易掌握的高层次的思想方法。“构造”是一种重要而灵活的思维方式,它没有固定的模式.要想用好它,需要有敏锐的观察、丰富的联想、灵活的构造、创造性的思维等能力,故有一定的难度.应用好构造思想解题的关键有二:一是要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行逻辑组合构造的方法有很多,其中以构造函数法、构造方程法、构造图形法、构造数列法、构造模型法、构造复数法等最为常见。下面介绍一些常用的构造方法。1.构造函数法在求解某些数学问题时,根据问题的条件,构想组合一种新的函数关系,使问题在新的观念下转化并利用函数的有关性质解决原问题是一种行之有效的解题手段。构造函数证(解)问题是一种创造性思维过程,具有较大的灵活性和技巧性。在运用过程中,应有目的、有意识地进行构造,始终“盯住”要证、要解的目标。【例1】证明:如果,那么证明:构造函数易证在R上是奇函数且单调递增+==lg1=0即:又是增函数即[例2]已知x,y,z∈(0,1),求证:x(1-y)+y(1-z)+z(1-x)分析:此题条件、结论均具有一定的对称性,然而难以直接证明,不妨用构造法一试。证:构造函数f(x)=(y+z-1)x+(yz-y-z+1) y,z∈(0,1),用心爱心专心∴f(0)=yz-y-z+1=(y-1)(z-1)>0f(1)=(y+z-1)+(yz-y-z+1)=yz>0而f(x)是一次函数,其图象是直线,∴由x∈(0,1)恒有f(x)>0即(y+z-1)x+(yz-y-z+1)>0整理可得x(1-y)+y(1-z)+z(1-x)<12、构造方程法有些数学问题,可以根据问题中存在的或隐含的等量关系构造方程,从而将问题转化为方程(组)来解决。构造方程解题体现了方程的观点,运用方程观点解题可归结为3个步骤:(1)将所面临的问题转化为方程问题;(2)解这个方程或讨论这个方程的有关性质(常用判别式与韦达定理),得出相应结论;(3)将方程的相应结论再返回为原问题的结论。【例3】设且,,求的范围解:由得(1)将(1)的两边平方并将代入得(2)由(1)(2)可知,是方程的两个不等的实根于是解得:即:对于较复杂的问题,就需根据条件进行框架的设计。为了运用判别式证明不等式,就需构思一个“一元二次方程”框架。【例4】求y=的值域。分析:求函数的值域的方法很多,判别式法是常用的一种,它的理论依据是将y=f(x)化为关于x的二次方程,那么方程若有实根,判别式0,由此可求得函数的值域,解:将y=变形为关于x的方程-(y+3)x+(1-y)=0当y1时,方程为关于x的二次方程所以-40,解得,当y=1时,x=0,此时。用心爱心专心于是y=的值域为。当然以上此题如果改为求证:方法也是一样的。即设y=3、构造图形法如果问题条件中的数量关系有明显的或隐含的几何意义与背景,或能以某种方式与几何图形建立起联系,则可考虑通过构造几何图形将题设中的数量关系直接在图形中得以实现,然后,借助于图形的性质在所构造的图形中寻求问题的结论。构造的图形,最好是简单而又熟悉其性质的图形。这些几何图形包括平面几何图形、立体几何图形及通过建立坐标系得到的解析几何图形。【例5】求函数的值域解析:其几何意义是平面内动点P(,0)到两定点M(2,3)和N(5,-1)的距离之和(如图1)为求其值域只要求其最值即可,易知当M,N,P三点共线(即P在线段MN上)时,取得最小值,,无最大值,故得函数的值域为图1【例6】、求函数的最值。分析:从几何意义上考虑把原解析式看作是动点P(cosx,sinx)与定点Q(3,0)连线的斜率。为此构造一个单位圆。探究单位圆上动点P与定点Q(3,0)直线的斜率问题。如图2,因为动点在单位圆上运动时处于极端状态,即为切点时直线斜率分别为最大最小,设切点分别为R、M,易知:用心爱心专心ͼ23-1-111RQMyxO即:最小值为,最大值为。4、构造向量法向量是新教...