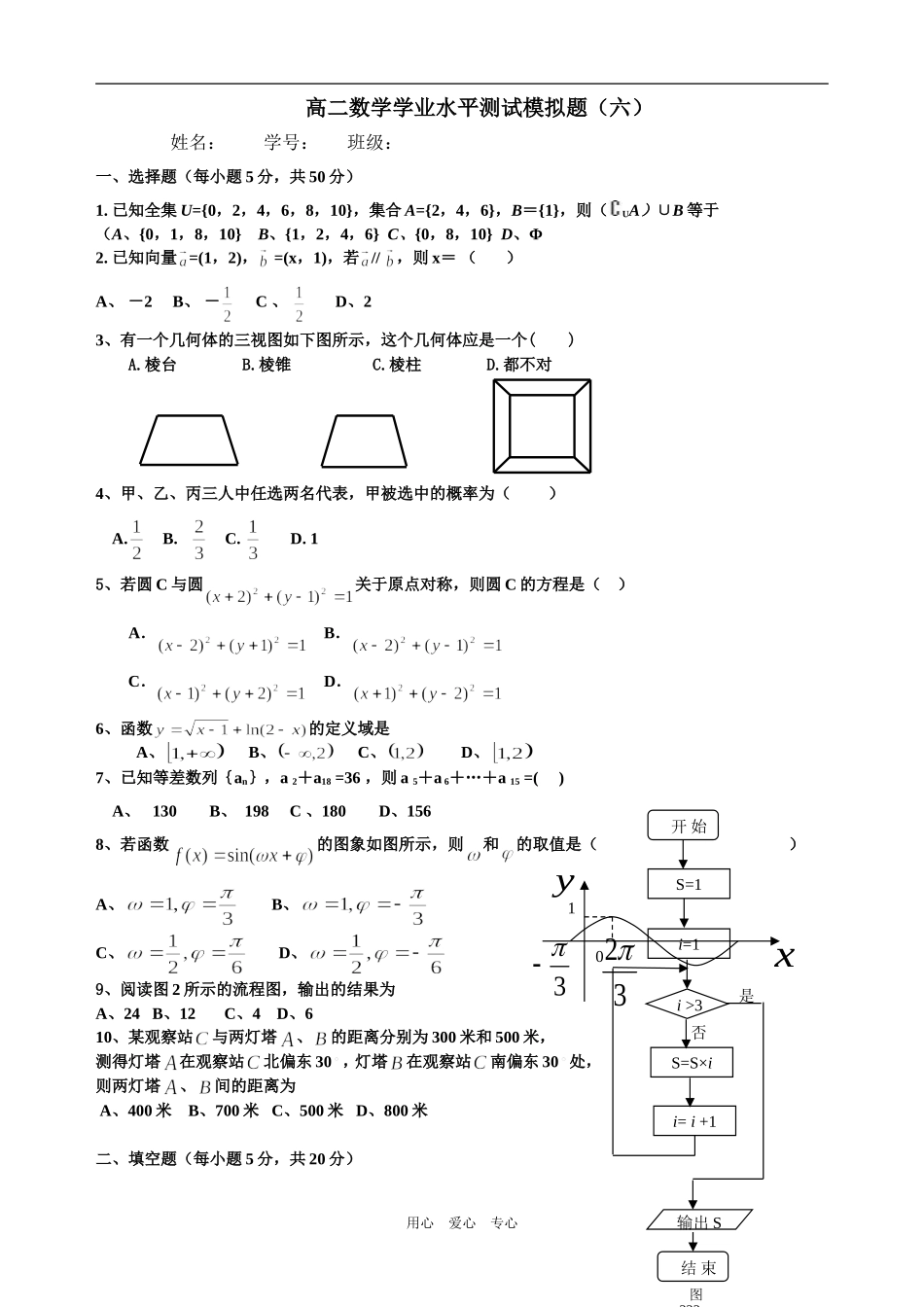
高二数学学业水平测试模拟题(六)姓名:学号:班级:一、选择题(每小题5分,共50分)1.已知全集U={0,2,4,6,8,10},集合A={2,4,6},B={1},则(UA)∪B等于(A、{0,1,8,10}B、{1,2,4,6}C、{0,8,10}D、Φ2.已知向量=(1,2),=(x,1),若//,则x=()A、-2B、-C、D、23、有一个几何体的三视图如下图所示,这个几何体应是一个()A.棱台B.棱锥C.棱柱D.都不对4、甲、乙、丙三人中任选两名代表,甲被选中的概率为()A.B.C.D.15、若圆C与圆关于原点对称,则圆C的方程是()A.B.C.D.6、函数的定义域是A、B、C、D、7、已知等差数列{an},a2+a18=36,则a5+a6+…+a15=()A、130B、198C、180D、1568、若函数的图象如图所示,则和的取值是()A、B、C、D、9、阅读图2所示的流程图,输出的结果为A、24B、12C、4D、610、某观察站与两灯塔、的距离分别为300米和500米,测得灯塔在观察站北偏东30,灯塔在观察站南偏东30处,则两灯塔、间的距离为A、400米B、700米C、500米D、800米二、填空题(每小题5分,共20分)用心爱心专心图222结束开始S=1i=1i>3S=S×ii=i+1输出S是否3023x1y11、sin,则tan=_____________。12、一个正方体棱长为a,则其外接球的体积为_________13、若,则当且仅当=时,函数的最大值为;14、已知x,y满足,则的最大值为.三、解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤)15、(满分10分)在等比数列中,,公比,前项和,求首项和项数.16、(满分12分)已知点A(1,-1),B(5,1),直线经过点A,且斜率为,(1)求直线的方程。(2)求以B为圆心,并且与直线相切的圆的标准方程。17、(满分14分)已知函数(1)求函数的最小正周期(2)求函数的单调递增区间(3)求函数的最大值,并求出对应的X值的取值集合。用心爱心专心18、(满分12分)在正方体ABCD-A1B1C1D1中,O为底面正方形ABCD的中心,M是线段AB的中点,.求证:(1)MO//平面ADD1A1(2)平面平面19、(满分10分)在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。(1)求取出的两个球上标号为相邻整数的概率;(2)求取出的两个球上标号之和能被3整除的概率。20、(满分12分)已知函数满足条件:①;②对一切,都有.(Ⅰ)求、的值;(Ⅱ)是否存在实数,使函数在区间上有最小值-5?若存在,请求出实数的值;若不存在,请说明理由.用心爱心专心MODCBAB1D1A1C12007年番禺区高二数学学业水平测试模拟题(六)参考答案一、选择题(本题共10小题,每小题5分,共60分)二、填空题(本题共4小题,共20分)11.-;12.;13、0;114.14用心爱心专心题号12345678910答案ACCBADBCDB三、解答题(本题共6小题,共80分)15、解:由题意有:把q=3代入,解得:所求的值为2,5。16、解:由直线方程点斜方程:直线过A点:即,整理得:3x+4y+1=0(2)由题意,与圆B相切,则圆心B与直线的距离为圆的半径。则:以B为圆心的圆的标准方程:。17、解(1)(2)即函数的增区间为(3)当时,,函数的最大值为1,此时18、证明:(1) 正方体ABCD-A1B1C1D1中,O为底面正方形ABCD的中心,M是线段AB的中点。∴OM//A1D,而OM平面ADD1A1,A1D平面ADD1A1,∴OM//平面ADD1A1.(2)在正方体ABCD-A1B1C1D1中,AA1⊥平面ABCD,BD平面ABCD,∴BD⊥AA1.在正方体ABCD中,BD⊥AC,且AA1AC=A,AC、AA1平面AA1C1C,∴BD⊥平面AA1C1C,∴BD平面A1BD,平面A1BD⊥平面A1ACC1.19、19.(本小题满分12分)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.(Ⅰ)求取出的两个球上标号为相邻整数的概率;(Ⅱ)求取出的两个球上标号之和能被3整除的概率.解法一:利用树状图可以列出从甲、乙两个盒子中各取出1个球的所有可能结果:用心爱心专心11234212343123441234可以看出,试验的所有可能结果数为16种.……4分(Ⅰ)所取两个小球上的标号为相邻整数的结果有1-2,2-1,2-3,3-2,3-4,4-3,共6种.……6分故所求概率.答:取出的两个小球上的标号为相邻整数的概率为...