3.1.5空间向量运算的坐标表示课时演练·促提升A组1.已知向量=(2,3,4),点A的坐标是(1,2,0),则点B的坐标是()A.(1,1,4)B.(3,5,4)C.(-1,1,-4)D.(3,6,3)解析:设点B的坐标为(x,y,z),由点A的坐标为(1,2,0),则=(x-1,y-2,z)=(2,3,4).即解得故点B的坐标为(3,5,4).答案:B2.向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),下列结论正确的是()A.a∥b,a⊥bB.a∥b,a⊥cC.a∥c,a⊥bD.以上都不对解析:由已知a·b=-2×2-3×0+4=0,∴a⊥b.又∵c=2a,∴a∥c.答案:C3.设A(3,3,1),B(1,0,5),C(0,1,0),则AB的中点M到C的距离|CM|的值为()A.B.C.D.解析:因为AB中点M,且C(0,1,0),所以,故M到C的距离为|CM|=||=.答案:C4.已知a=(1,0,1),b=(x,1,2),且a·b=3,则向量a与b的夹角为()A.B.C.D.解析:∵a·b=x+2=3,∴x=1,∴b=(1,1,2),∴cos
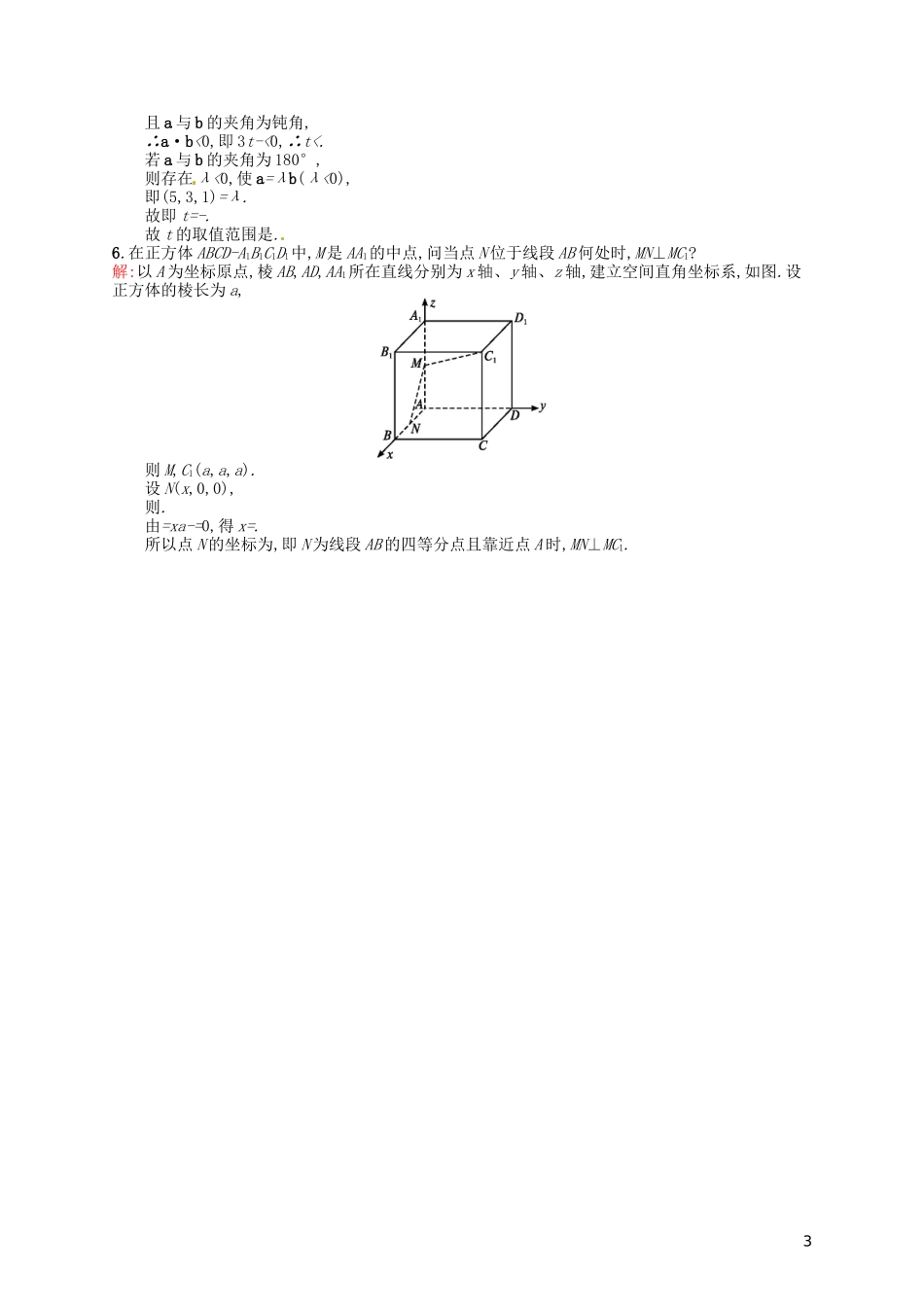
=.∴a与b的夹角为.答案:D5.在△ABC中,∠C=90°,A(1,2,-3k),B(-2,1,0),C(4,0,-2k),则k的值为()A.B.-C.2D.±解析:∵=(-6,1,2k),=(-3,2,-k),∴=(-6)×(-3)+2+2k×(-k)=-2k2+20.∵∠C=90°,∴CA⊥CB,∴=0,即-2k2+20=0,∴k=±.答案:D6.与向量a=(2,-1,2)共线且满足a·x=-18的向量x的坐标是.解析:因为x与a共线,所以可设x=ka,由a·x=-18,得a·ka=k|a|2=k()2=9k,所以9k=-18,k=-2.所以x=-2a=(-4,2,-4).答案:(-4,2,-4)7.已知a=(2,-3,0),b=(k,0,3),若a,b的夹角为120°,则k=.解析:由已知可得cos120°=,解得k=-(k=舍去).答案:-8.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的面积是.解析:∵=(5,1,-7),=(2,-3,1),∴=10-3-7=0.∴,即AC⊥BC.∴S△ABC=|·||=.答案:9.已知a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),a∥b,b⊥c,求:(1)a,b,c;(2)(a+c)与(b+c)所成角的余弦值.解:(1)因为a∥b,所以,解得x=2,y=-4,这时a=(2,4,1),b=(-2,-4,-1).又因为b⊥c,所以b·c=0,即-6+8-z=0,解得z=2,故c=(3,-2,2).(2)由(1)得,(a+c)=(5,2,3),(b+c)=(1,-6,1),因此(a+c)与(b+c)所成角的余弦值cosθ==-.110.在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为D1D,BD的中点,G在棱CD上,且CG=CD,H为C1G的中点.(1)求EF与C1G所成角的余弦值;(2)求FH的长.解:如图,以D为坐标原点,建立空间直角坐标系Dxyz,则有E,F,C(0,1,0),C1(0,1,1),B1(1,1,1),G.(1)∵-(0,1,1)=,∴||=.又∵,∴||=.∴×0+×(-1)=.∴cos<>=.(2)∵F,H,∴.∴||=.B组1.若△ABC的顶点分别为A(1,-1,2),B(5,-6,2),C(1,3,-1),则AC边上的高BD等于()A.5B.C.4D.2解析:设=λ,又=(0,4,-3),则=(0,4λ,-3λ).又∵=(-4,5,0),∴=(-4,4λ+5,-3λ).由=0,得4(4λ+5)+9λ=0,解得λ=-,∴,∴||=5.答案:A2.已知a=(1-t,1-t,t),b=(2,t,t),则|b-a|的最小值是()A.B.C.D.解析:由已知,得b-a=(2,t,t)-(1-t,1-t,t)=(1+t,2t-1,0),∴|b-a|==,∴当t=时,|b-a|取得最小值,最小值为.答案:C3.若a=(2,3,-1),b=(-2,1,3),则以a,b为邻边的平行四边形的面积是.解析:|a|=,|b|=.设θ为a与b的夹角,则cosθ==-,所以sinθ=.所以S平行四边形=|a||b|sinθ=14×=6.答案:64.已知A(1,0,0),B(0,1,0),C(0,0,2).(1)若,求点D的坐标;(2)问是否存在实数α,β,使得=α+β成立?若存在,求出α,β的值;若不存在,说明理由.解:(1)设D(x,y,z),则=(-x,1-y,-z),=(-1,0,2),=(-x,-y,2-z),=(-1,1,0),因为,所以解得即D(-1,1,2).(2)依题意=(-1,1,0),=(-1,0,2),=(0,-1,2),假设存在实数α,β,使得=α+β成立,则有(-1,0,2)=α(-1,1,0)+β(0,-1,2)=(-α,α-β,2β),所以故存在α=β=1,使得=α+β成立.5.已知a=(5,3,1),b=,若a与b的夹角为钝角,求实数t的取值范围.解:∵a·b=5×(-2)+3t+1×=3t-,2且a与b的夹角为钝角,∴a·b<0,即3t-<0,∴t<.若a与b的夹角为180°,则存在λ<0,使a=λb(λ<0),即(5,3,1)=λ.故即t=-.故t的取值范围是.6.在正方体ABCD-A1B1C1D1中,M是AA1的中点,问当点N位于线段AB何处时,MN⊥MC1?解:以A为坐标原点,棱AB,AD,AA1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图.设正方体的棱长为a,则M,C1(a,a,a).设N(x,0,0),则.由=xa-=0,得x=.所以点N的坐标为,即N为线段AB的四等分点且靠近点A时,MN⊥MC1.3