高中数学 课后作业7 直线与平面平行的判定 北师大版必修2-北师大版高一必修2数学试题VIP免费

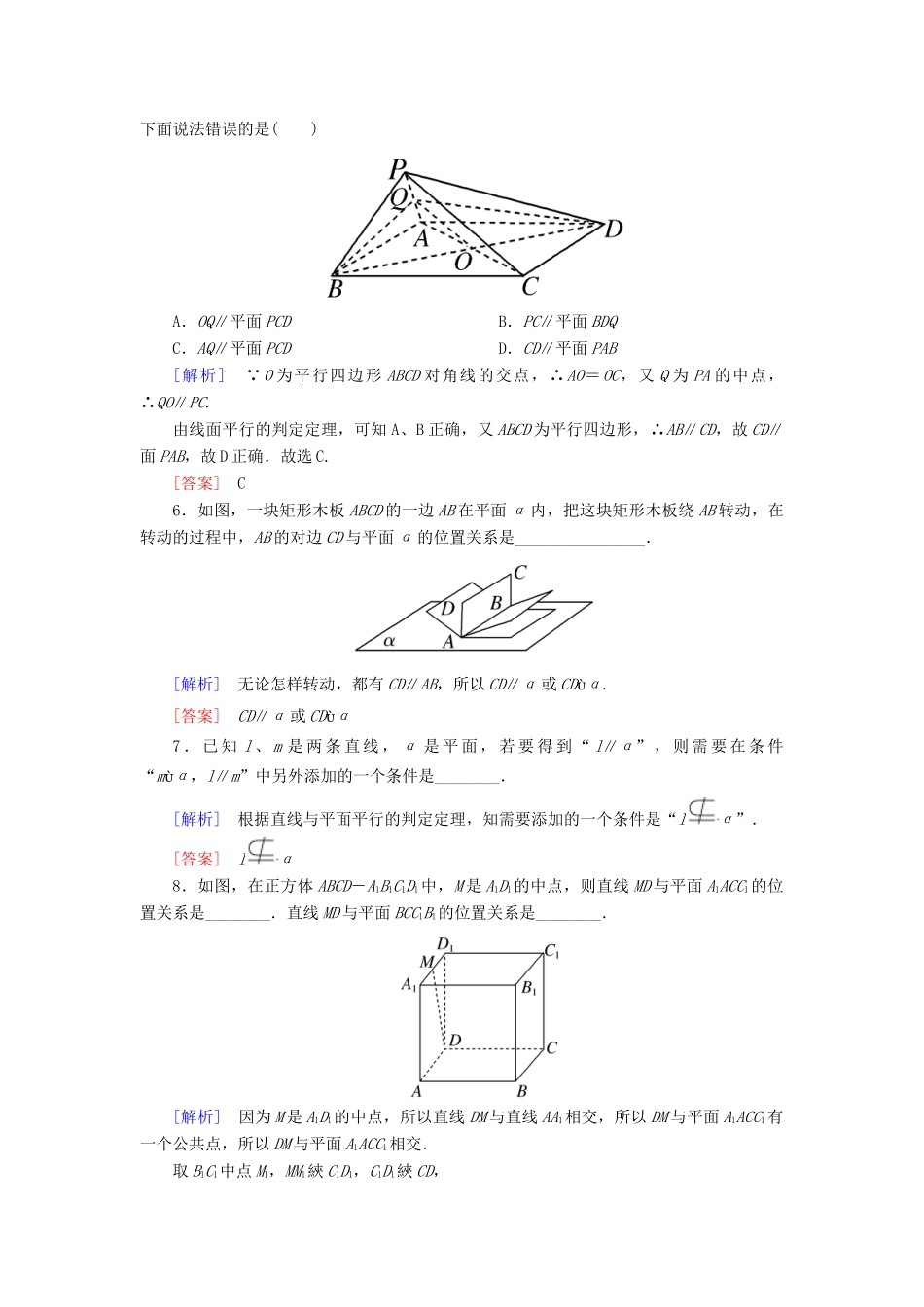
课后作业(七)(时间45分钟)学业水平合格练(时间20分钟)1．已知a，b是两条相交直线，a∥α，则b与α的位置关系是()A．b∥αB．b与α相交C．bαD．b∥α或b与α相交[解析]可能平行，此时a与b确定的平面与平面α平行；也可能相交，此时a与b确定的平面与平面α相交．故选D.[答案]D2．直线a，b为异面直线，过直线a与直线b平行的平面()A．有且只有一个B．有无数多个C．有且只有一个或不存在D．不存在[解析]取直线a上任一点A，则点A和直线b确定一个平面记为β，在β内过A点作直线c∥b，由a∩c＝A，则直线a、c确定唯一的平面记为α， c∥b，cα，bα.∴b∥α有且仅有一个．故选A.[答案]A3．若M、N分别是△ABC边AB、AC的中点，MN与过直线BC的平面β的位置关系是()A．MN∥βB．MN与β相交或MNβC．MN∥β或MNβD．MN∥β或MN与β相交或MNβ[解析] MN是△ABC的中位线，∴MN∥BC， 平面β过直线BC，∴若平面β过直线MN，符合要求；若平面β不过直线MN，由线线平行的判定定理知MN∥β.故选C.[答案]C4．如果直线l、m与平面α、β、γ满足：β∩γ＝l，m∥l，mα，则必有()A．l∥αB．lαC．m∥β且m∥γD．m∥β或m∥γ[解析]当平面α与β，γ都相交或者与一个相交时， β∩γ＝l，m∥l，mα且mβ，mγ，∴m∥β，m∥γ；当平面α与平面β或者γ相交于m时，则m∥β或者m∥γ；故选D.[答案]D5．如图P为平行四边形ABCD所在平面外一点，Q为PA的中点，O为AC与BD的交点，下面说法错误的是()A．OQ∥平面PCDB．PC∥平面BDQC．AQ∥平面PCDD．CD∥平面PAB[解析] O为平行四边形ABCD对角线的交点，∴AO＝OC，又Q为PA的中点，∴QO∥PC.由线面平行的判定定理，可知A、B正确，又ABCD为平行四边形，∴AB∥CD，故CD∥面PAB，故D正确．故选C.[答案]C6．如图，一块矩形木板ABCD的一边AB在平面α内，把这块矩形木板绕AB转动，在转动的过程中，AB的对边CD与平面α的位置关系是________________．[解析]无论怎样转动，都有CD∥AB，所以CD∥α或CDα.[答案]CD∥α或CDα7．已知l、m是两条直线，α是平面，若要得到“l∥α”，则需要在条件“mα，l∥m”中另外添加的一个条件是________．[解析]根据直线与平面平行的判定定理，知需要添加的一个条件是“lα”．[答案]lα8．如图，在正方体ABCD－A1B1C1D1中，M是A1D1的中点，则直线MD与平面A1ACC1的位置关系是________．直线MD与平面BCC1B1的位置关系是________．[解析]因为M是A1D1的中点，所以直线DM与直线AA1相交，所以DM与平面A1ACC1有一个公共点，所以DM与平面A1ACC1相交．取B1C1中点M1，MM1綊C1D1，C1D1綊CD，∴四边形DMM1C为平行四边形，∴DM綊CM1， DM平面BCC1B1，CM1平面BCC1B1，∴DM∥平面BCC1B1.[答案]相交平行9．如图，四边形ABCD是平行四边形，S是平面ABCD外一点，M为SC的中点，求证：SA∥平面MDB.[证明]连接AC交BD于点O，连接OM. M为SC的中点，O为AC的中点，∴OM∥SA， OM平面MDB，SA⃘平面MDB，∴SA∥平面MDB.10.如图所示，空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．求证：(1)EH∥平面BCD；(2)BD∥平面EFGH.[证明](1) EH为△ABD的中位线，∴EH∥BD. EH平面BCD，BD平面BCD，∴EH∥平面BCD.(2) BD∥EH，BD平面EFGH，EH平面EFGH，∴BD∥平面EFGH.应试能力等级练(时间25分钟)11．如图，正方体ABCD－A1B1C1D1中，E，F分别为棱AB，CC1的中点，在平面ADD1A1内且与平面D1EF平行的直线()A．不存在B．有1条C．有2条D．有无数条[解析]由题设知平面ADD1A1与平面D1EF有公共点D1，由平面的基本性质中的公理知必有过该点的公共线l，在平面ADD1A1内与l平行的线有无数条，且它们都不在平面D1EF内，由线面平行的判定定理知它们都与面D1EF平行．故选D.[答案]D12．如果AB、BC、CD是不在同一平面内的三条线段，则经过它们中点的平面和直线AC的位置关系是()A．平行B．相交C．AC在此平面内D．平行或相交[解析]把这三条线段放在正方体内，如图．显然AC∥EF，AC⃘平面EFG.EF平面EFG，故AC∥平面EFG.故选A.[答案]A13．已知直线b，平面α，有以下条件：①b与α内一条直线平行；②b与α内所有直线都没有公共点；③b与α无公共...