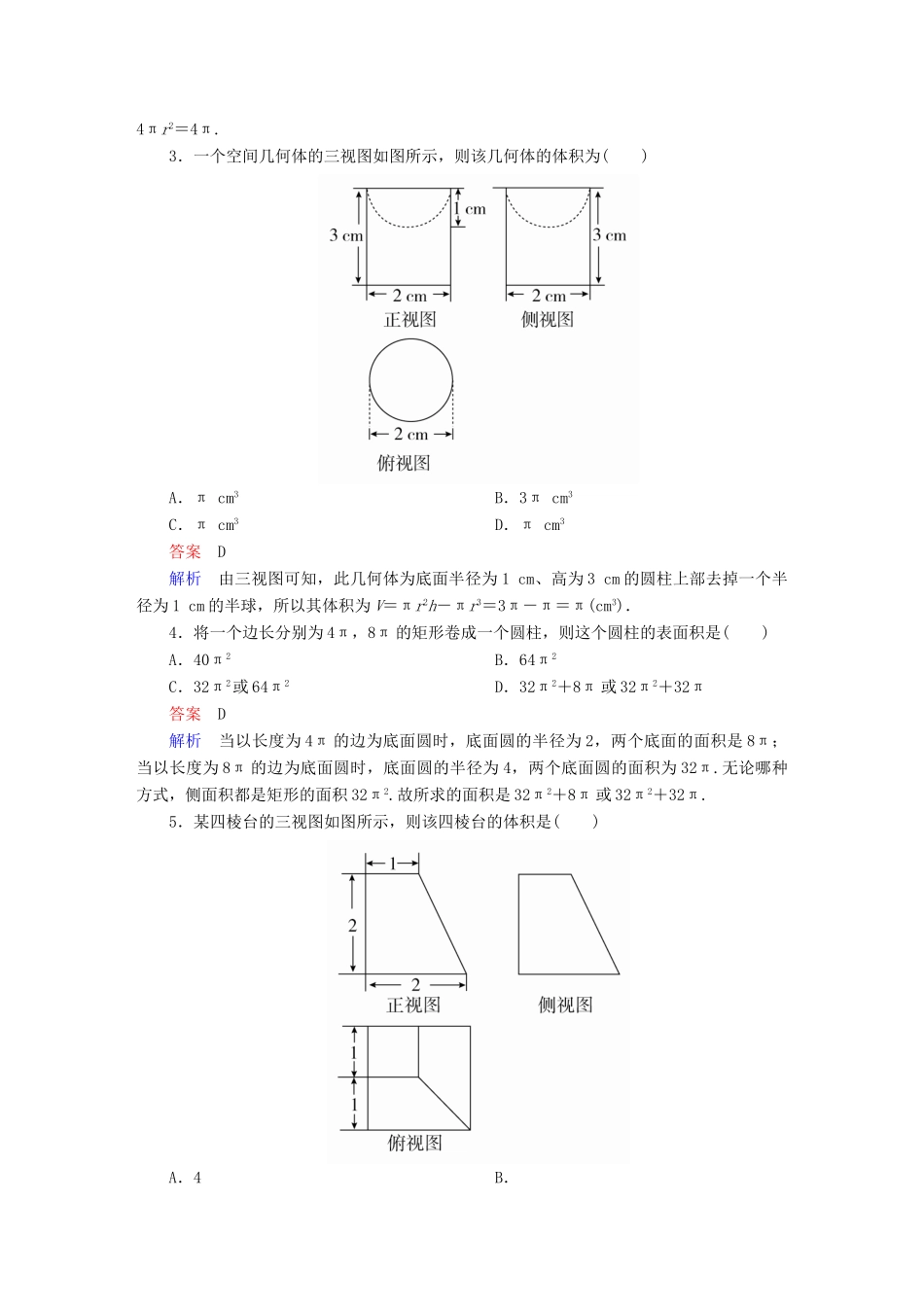
考点测试41空间几何体的表面积和体积一、基础小题1.如图,一个空间几何体的正视图、侧视图都是面积为,一个内角为60°的菱形,俯视图为正方形,那么这个几何体的表面积为()A.2B.4C.8D.4答案D解析由三视图知,原几何体为两个四棱锥的组合体,其中四棱锥的底面边长为1,斜高为1,所以这个几何体的表面积为S=×1×1×8=4.2.一个正方体的体积是8,则这个正方体的内切球的表面积是()A.8πB.6πC.4πD.π答案C解析设正方体的棱长为a,则a3=8,∴a=2.而此正方体的内切球直径为2,∴S表=4πr2=4π.3.一个空间几何体的三视图如图所示,则该几何体的体积为()A.πcm3B.3πcm3C.πcm3D.πcm3答案D解析由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=πr2h-πr3=3π-π=π(cm3).4.将一个边长分别为4π,8π的矩形卷成一个圆柱,则这个圆柱的表面积是()A.40π2B.64π2C.32π2或64π2D.32π2+8π或32π2+32π答案D解析当以长度为4π的边为底面圆时,底面圆的半径为2,两个底面的面积是8π;当以长度为8π的边为底面圆时,底面圆的半径为4,两个底面圆的面积为32π.无论哪种方式,侧面积都是矩形的面积32π2.故所求的面积是32π2+8π或32π2+32π.5.某四棱台的三视图如图所示,则该四棱台的体积是()A.4B.C.D.6答案B解析依题意,所求几何体是一个四棱台,其中上底面是边长为1的正方形、下底面是边长为2的正方形,高是2,因此其体积等于×(12+22+)×2=,故选B.6.某几何体的正(主)视图和侧(左)视图如图所示,则该几何体的体积不可能是()A.B.C.D.1答案D解析寻找两个极限状态,一是底面无面积,此时V=0;二是底面面积最大时,底面为正方形,此时V=×1×1×2=,因此该几何体的体积0