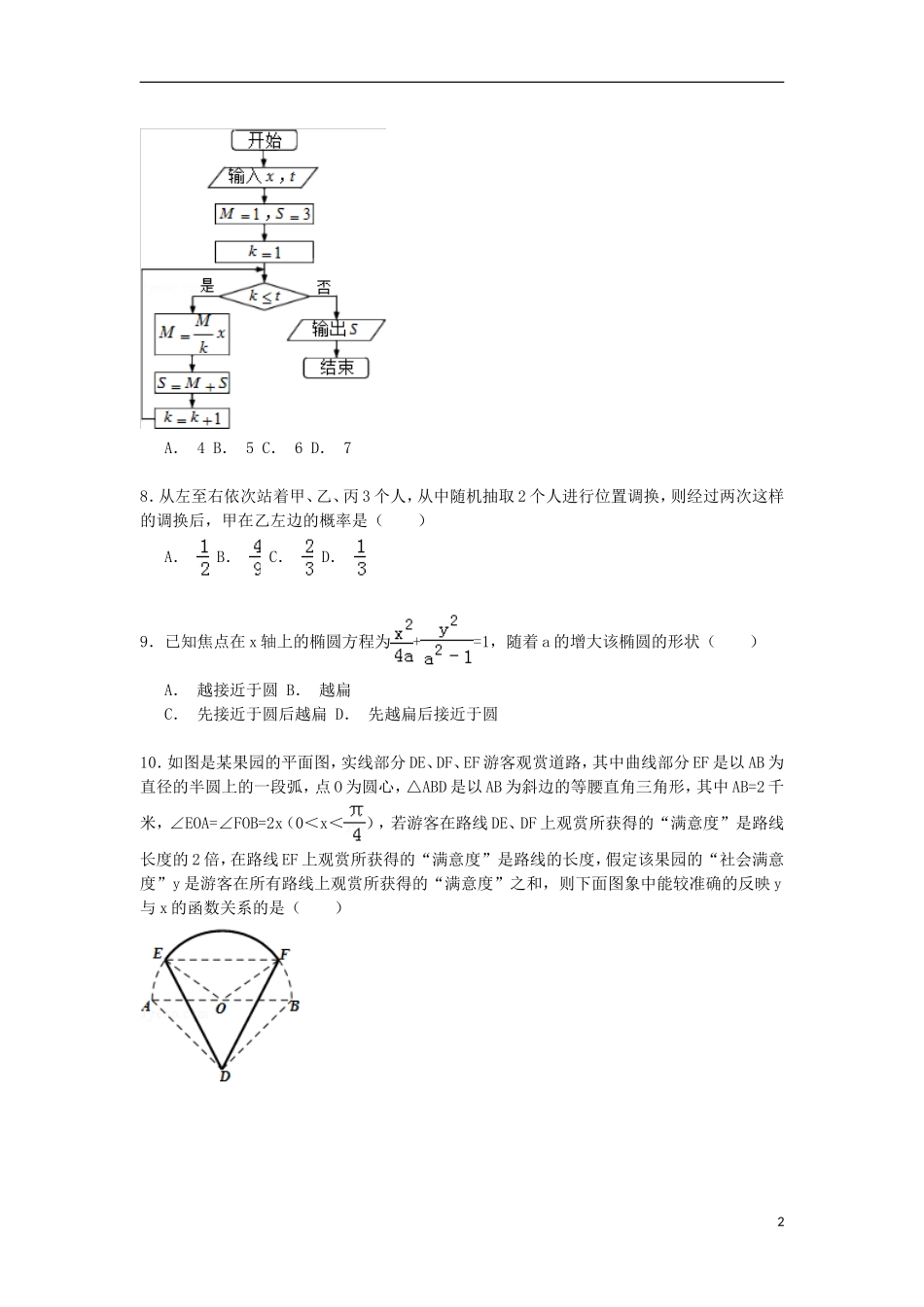
2015年山东省东营市高考数学二模试卷(理科)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.将正确答案填写在答题卷相应位置.1.已知i是虚数单位,则=()A.1﹣2iB.2﹣iC.2+iD.1+2i2.若集合A={x|},B={x|x2<2x},则A∩B=()A.{x|0<x<1}B.{x|0≤x<1}C.{x|0<x≤1}D.{x|0≤x≤1}3.已知α,β角的终边均在第一象限,则“α>β”是“sinα>sinβ”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知函数f(x+1)是偶函数,当x∈(1,+∞)时,函数f(x)=sinx﹣x,设a=f(﹣),b=f(3),c=f(0),则a、b、c的大小关系为()A.b<a<cB.c<a<bC.b<c<aD.a<b<c5.一个几何体的三视图如图所示,该几何体外接球的表面积为()A.9πB.C.8πD.7π6.已知{an}是首项为1的等比数列,Sn是{an}的前n项和,且9S3=S6,则数列的前5项和为()A.或5B.或5C.D.7.执行如图所示的程序框图,若输入的x,t均为2,则输出的S=()1A.4B.5C.6D.78.从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换后,甲在乙左边的概率是()A.B.C.D.9.已知焦点在x轴上的椭圆方程为+=1,随着a的增大该椭圆的形状()A.越接近于圆B.越扁C.先接近于圆后越扁D.先越扁后接近于圆10.如图是某果园的平面图,实线部分DE、DF、EF游客观赏道路,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<),若游客在路线DE、DF上观赏所获得的“满意度”是路线长度的2倍,在路线EF上观赏所获得的“满意度”是路线的长度,假定该果园的“社会满意度”y是游客在所有路线上观赏所获得的“满意度”之和,则下面图象中能较准确的反映y与x的函数关系的是()2A.B.C.D.二.填空题:本大题共5小题,每小题5分,共25分.11.已知9a=3,lgx=a则x=.12.的展开式中的常数项为a,则直线y=ax与曲线y=x2围成图形的面积为.13.已知若f[f(x0)]=3,则x0=.14.设x,t满足约束条件,若目标函数z=4ax+by(a>0,b>0)的最大值为8,则a=时,+取得最小值.15.在平面直角坐标系中,O为原点A(﹣1,0),B(0,),C(3,0),动点D满足||=1,则||的最大值是.三.解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.在△ABC中,三个内角A,B,C的对边分别为a,b,c,其中c=2,且==.(Ⅰ)求a,b,C.(Ⅱ)如右图,设圆O过A,B,C三点,点P位于劣弧上,记∠PAB=θ,求△PAC面积最大值.317.现有两种投资方案,一年后投资盈亏的情况如下:(1)投资股市:投资结果获利40%不赔不赚亏损20%概率(2)购买基金:投资结果获利20%不赔不赚亏损10%概率pq(Ⅰ)当时,求q的值;(Ⅱ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于,求p的取值范围;(Ⅲ)丙要将家中闲置的10万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知,,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?给出结果并说明理由.18.已知正项数列{an},其前n项和Sn满足,且a2是a1和a7的等比中项.(Ⅰ)求数列的通项公式;(Ⅱ)符号[x]表示不超过实数x的最大整数,记,求.19.在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.(Ⅰ)证明:BC⊥AB1;(Ⅱ)若OC=OA,求直线C1D与平面ABC所成角的正弦值.420.设A,B是椭圆W:+=1上不关于坐标轴对称的两个点,直线AB交x轴于点M(与点A,B不重合),O为坐标原点.(Ⅰ)如果点M是椭圆W的右焦点,线段MB的中点在y轴上,求直线AB的方程;(Ⅱ)设N为x轴上一点,且•=4,直线AN与椭圆W的另外一个交点为C,证明:点B与点C关x轴对称.21.已知函数.(Ⅰ)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;(Ⅱ)当x>0时,恒成立,求整数k的最大值;(Ⅲ)试证明:(1...