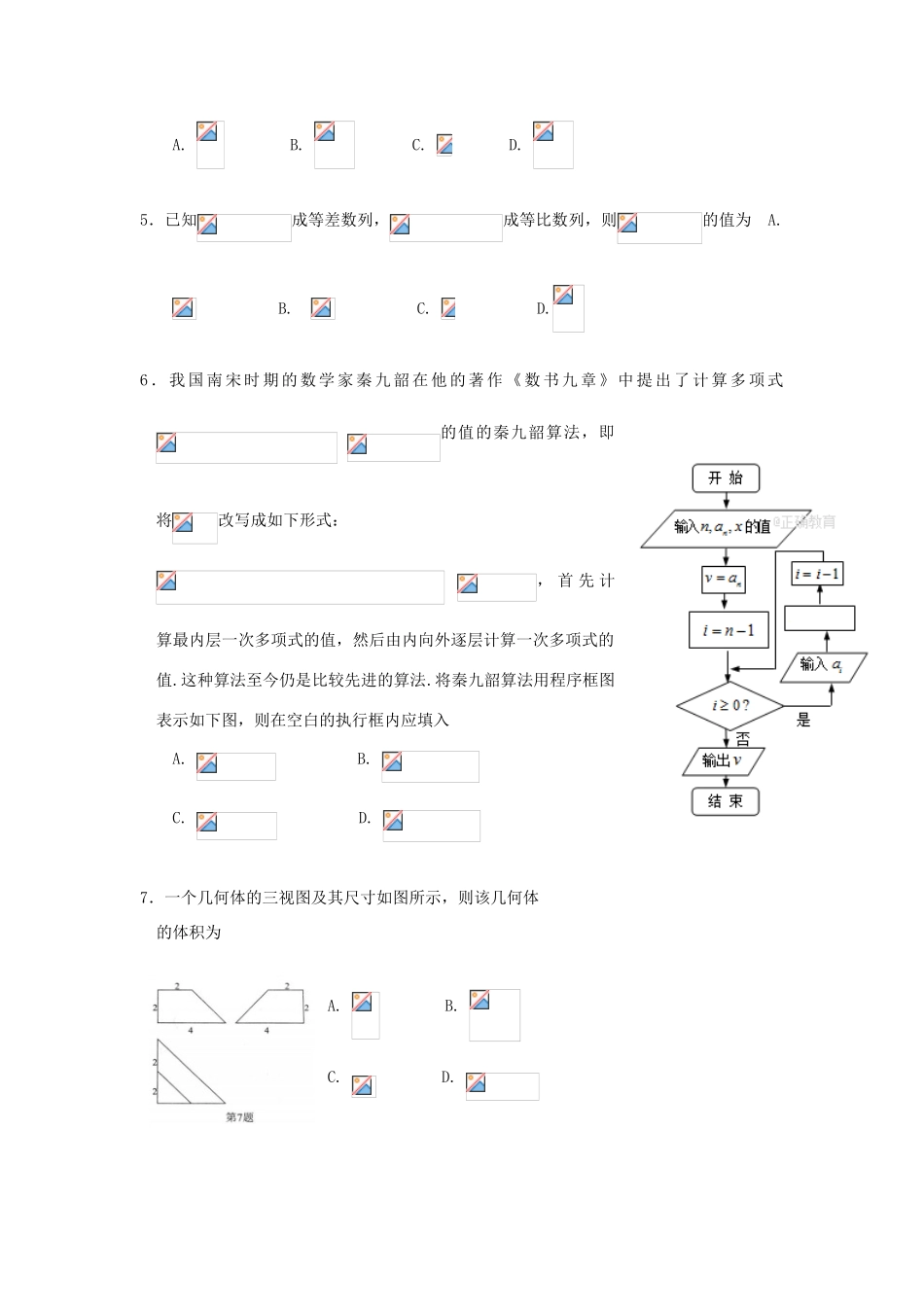
湖北省武汉市蔡甸区2017届高三数学第三次模拟考试试题理考试时间:2017年5月17日15:00——17:00试卷满分:150分注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至6页.2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成,答在本试题上无效.4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数满足,其中为虚数单位,则在复平面内所对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限2.已知集合,,全集,则等于A.B.C.D.3.若的展开式中的系数为30,则的值为A.B.C.D.4.如图,在平面直角坐标系中,角的顶点与坐标原点重合,始边与轴的非负半轴重合,它们的终边分别与单位圆相交于两点,若点的坐标分别为和,则的值为A.B.C.D.5.已知成等差数列,成等比数列,则的值为A.B.C.D.6.我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式的值的秦九韶算法,即将改写成如下形式:,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值.这种算法至今仍是比较先进的算法.将秦九韶算法用程序框图表示如下图,则在空白的执行框内应填入A.B.C.D.7.一个几何体的三视图及其尺寸如图所示,则该几何体的体积为A.B.C.D.8.已知,给出下列四个命题:其中真命题的是A.B.C.D.9.在中,是斜边上一点,且满足:,点在过点的直线上,若,,则的最小值为A.2B.C.3D.10.如图,直三棱柱中,,,,外接球的球心为,点是侧棱上的一个动点.有下列判断:①直线与直线是异面直线;②一定不垂直;③三棱锥的体积为定值;④的最小值为.其中正确的个数是A.1B.2C.3D.411.已知为直角坐标系的坐标原点,双曲线上有一点(),点在轴上的射影恰好是双曲线的右焦点,过点作双曲线两条渐近线的平行线,与两条渐近线的交点分别为,,若平行四边形的面积为1,则双曲线的标准方程是A.B.C.D.12.已知函数是定义在上的奇函数,且当时,,则对任意,函数的零点个数至多有A.3个B.4个C.6个D.9个第II卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.13.在区间上随机地取两个数,则事件“”发生的概率为____________.14.将函数的图象沿轴向右平移个单位长度后得到函数的图象,若函数的图象关于轴对称,则当取最小的值时,__________.15.设抛物线()的焦点为,准线为.过焦点的直线分别交抛物线于两点,分别过作的垂线,垂足.若,且三角形的面积为,则的值为___________.16.设,在上恒成立,则的最大值为.三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤17、(本小题满分12分).已知函数的一段图象如图所示.(1)求函数的解析式;(2)若函数在轴右侧的极小值点的横坐标组成数列,设右侧的第一个极小值点的横坐标为首项,试求数列的前项和.18、(本小题满分12分)已知6只小白鼠有1只被病毒感染,需要通过对其化验病毒来确定是否感染.下面是两种化验方案:方案甲:逐个化验,直到能确定感染为止.方案乙:将6只分为两组,每组三个,并将它们混合在一起化验,若存在病毒,则表明感染在这三只当中,然后逐个化验,直到确定感染为止;若结果不含病毒,则在另外一组中逐个进行化验.(1)求依据方案乙所需化验恰好为2次的概率.(2)首次化验化验费为10元,第二次化验化验费为8元,第三次及其以后每次化验费都是6元,列出方案甲所需化验费用的分布列,并估计用方案甲平均需要体验费多少元?19、(本小题满分12分)如图,三棱柱中,,,分别为棱的中点.(1)在平面内过点作平面交于点,并写出作图步骤,但不要求证明.(2)若侧面侧面,求直线与平面所成角的正弦值.20、(本小题满分12分)已知点,点是直线上的动点,过作直线,,线段的垂直平分线与交于点.(1)求点的轨迹的方程;(2)若点是直线上两个不同的点,且的内切圆方程为,直线的斜率为,求的取值范围.2...