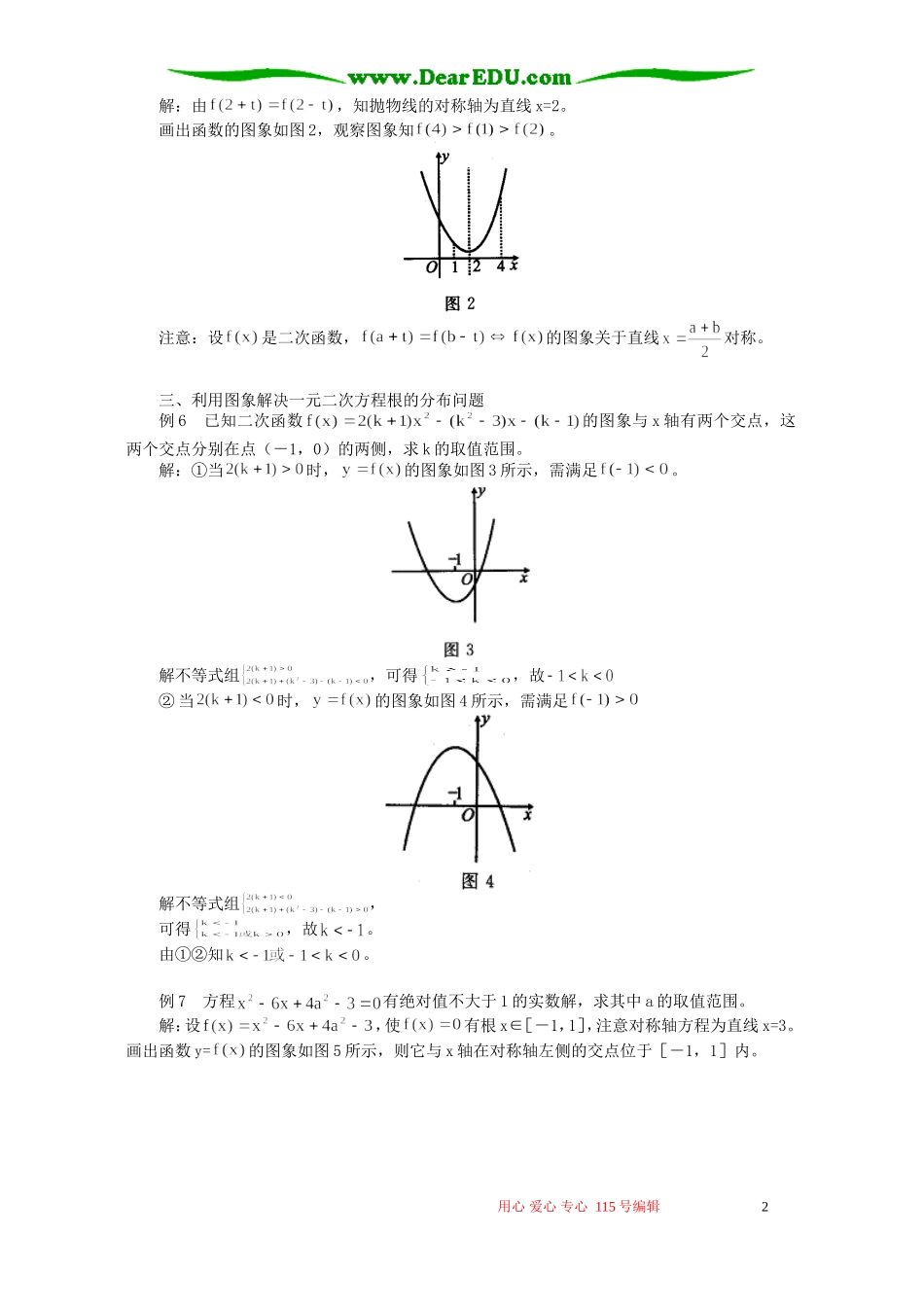
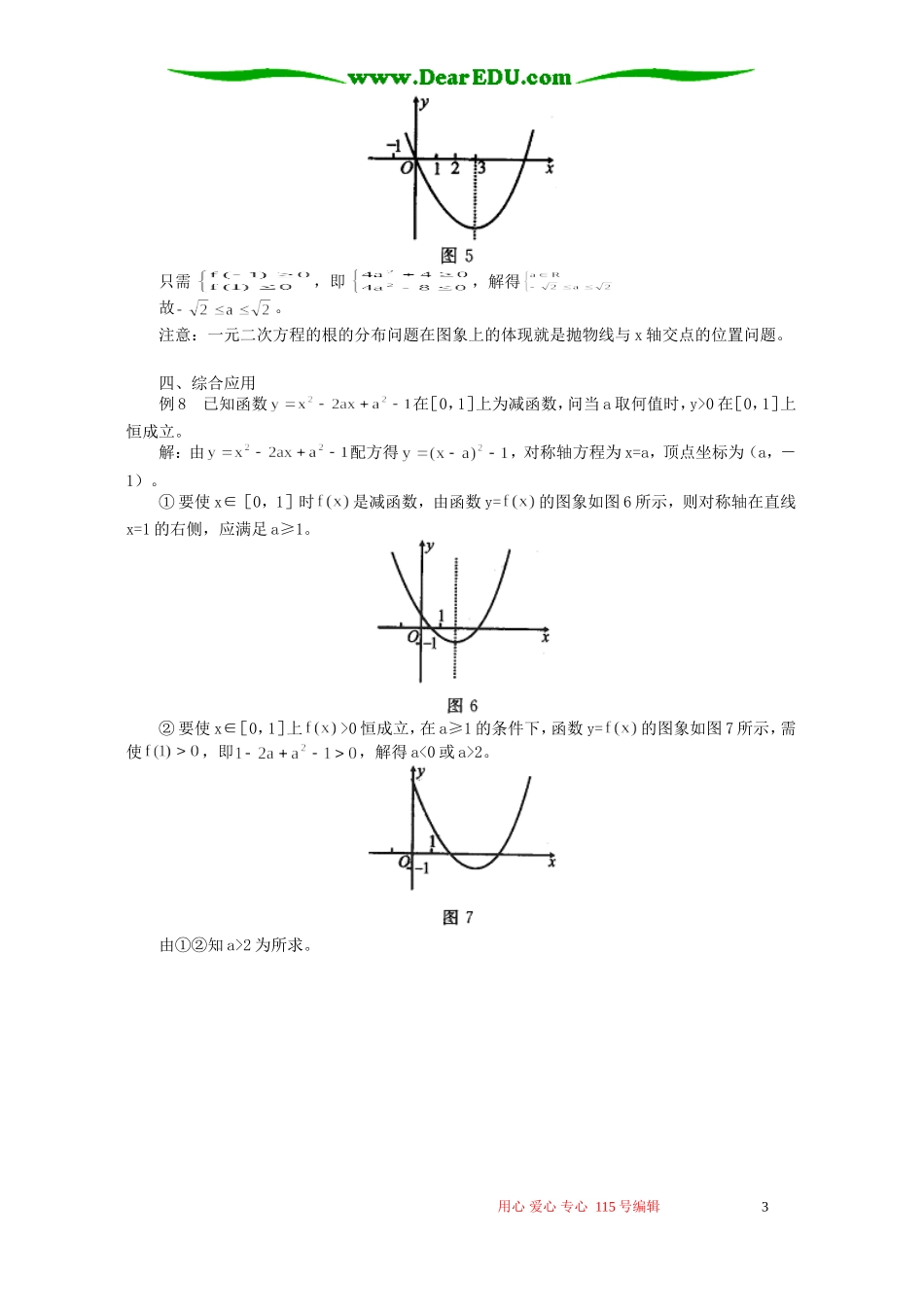
利用图象解决与二次函数相关的问题何乃忠何爽初中已经学习了一元二次方程、二次函数的图象和性质,这些内容是高中学习函数的重要基础。高中数学并没有再安排二次函数的课题。二次函数的内容穿插到各章节之中,遇到的问题比初中复杂,难度变大,同学们感到困难。本文介绍怎样通过数形结合的方法,利用二次函数的图象解决与二次函数相关的问题。一、利用配方法和函数的图象求二次函数的值域及其变式例1已知,求此函数的值域。解:,画出函数的图象如图1。图1当x=0时,f(x)有最大值;当x=2时,有最小值。故此函数的值域为[-8,-4]。注意:解决上述问题的步骤是:①配方,②本着先“虚”(定义域外)后“实”(定义域内)的原则画出图象,③根据“上大下小”的原则确定函数的值域。例2已知二次方程在[0,3]上有解,求实数a的取值范围。错解:由,得即为所求。分析:上述解法只保证方程有解,不保证解在[0,3]内。事实上,原方程在[0,3]上有解时函数的值存在。由例1知a∈[―8,―4]例3已知对任意x∈[0,3],恒成立,求实数a的取值范围。解:由原不等式得设,由例1知t∈[-8,-4]又对任意x∈[0,3],a>t恒成立,故。二、利用图象解决与二次函数性质相关的问题例4函数在区间[1,2]上存在反函数的充要条件是()。A、B、C、D、解:①当抛物线的对称轴x=a在区间[1,2]的左侧,即a≤1时,函数单调递增。②当抛物线的对称轴x=a在区间[1,2]的右侧,即a≥2时,函数单调递减。由①②知在[1,2]上存在反函数的充要条件是,应选D。例5如果函数对任意实数t都有,那么从大到小的排序为_________。用心爱心专心115号编辑1解:由,知抛物线的对称轴为直线x=2。画出函数的图象如图2,观察图象知。注意:设是二次函数,的图象关于直线对称。三、利用图象解决一元二次方程根的分布问题例6已知二次函数的图象与x轴有两个交点,这两个交点分别在点(-1,0)的两侧,求k的取值范围。解:①当时,的图象如图3所示,需满足。解不等式组,可得,故②当时,的图象如图4所示,需满足解不等式组,可得,故。由①②知。例7方程有绝对值不大于1的实数解,求其中a的取值范围。解:设,使有根x∈[-1,1],注意对称轴方程为直线x=3。画出函数y=的图象如图5所示,则它与x轴在对称轴左侧的交点位于[-1,1]内。用心爱心专心115号编辑2只需,即,解得故。注意:一元二次方程的根的分布问题在图象上的体现就是抛物线与x轴交点的位置问题。四、综合应用例8已知函数在[0,1]上为减函数,问当a取何值时,y>0在[0,1]上恒成立。解:由配方得,对称轴方程为x=a,顶点坐标为(a,-1)。①要使x∈[0,1]时是减函数,由函数y=的图象如图6所示,则对称轴在直线x=1的右侧,应满足a≥1。②要使x∈[0,1]上>0恒成立,在a≥1的条件下,函数y=的图象如图7所示,需使,即,解得a<0或a>2。由①②知a>2为所求。用心爱心专心115号编辑3