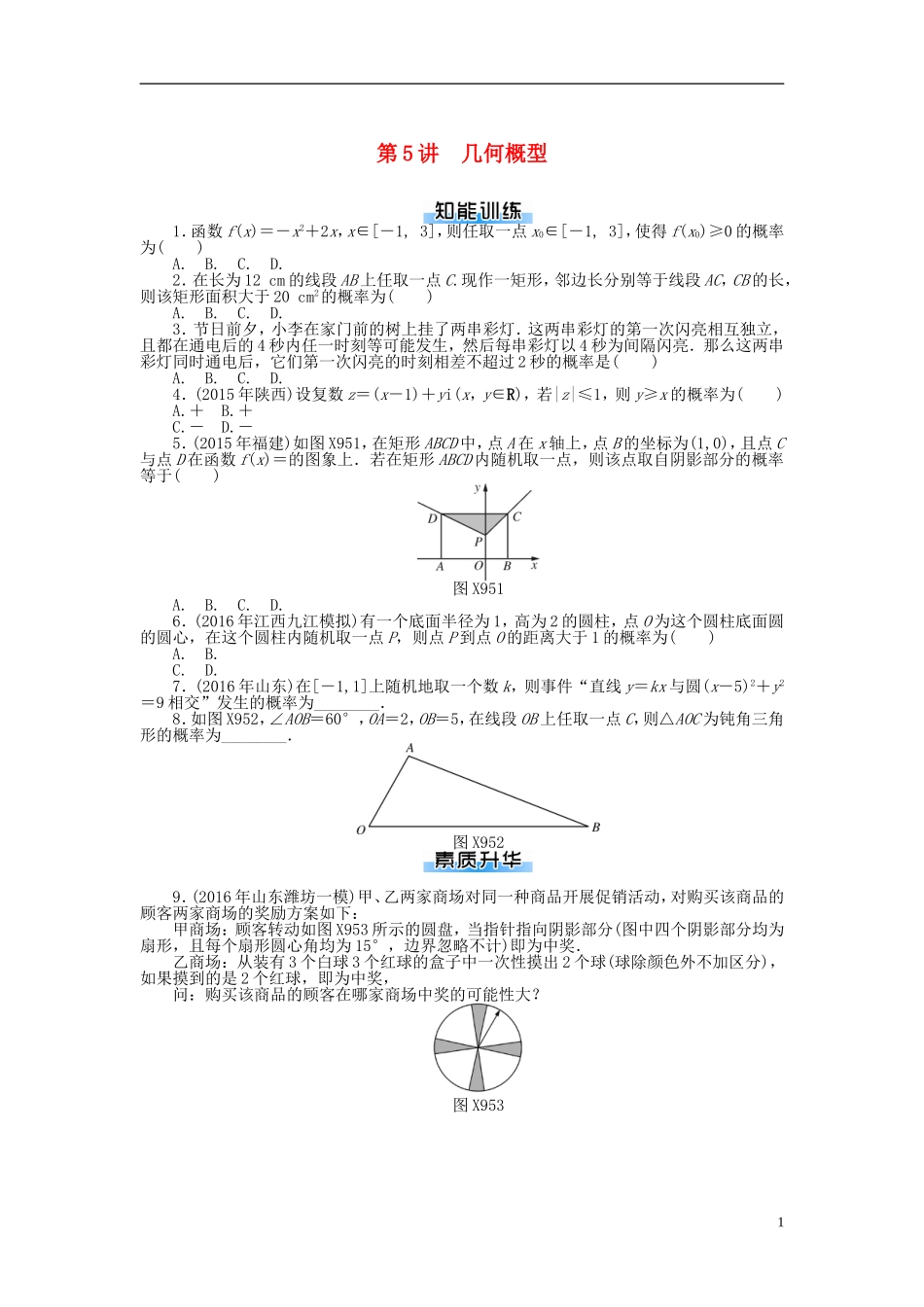
第5讲几何概型1.函数f(x)=-x2+2x,x∈[-1,3],则任取一点x0∈[-1,3],使得f(x0)≥0的概率为()A.B.C.D.2.在长为12cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积大于20cm2的概率为()A.B.C.D.3.节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是()A.B.C.D.4.(2015年陕西)设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为()A.+B.+C.-D.-5.(2015年福建)如图X951,在矩形ABCD中,点A在x轴上,点B的坐标为(1,0),且点C与点D在函数f(x)=的图象上.若在矩形ABCD内随机取一点,则该点取自阴影部分的概率等于()图X951A.B.C.D.6.(2016年江西九江模拟)有一个底面半径为1,高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,则点P到点O的距离大于1的概率为()A.B.C.D.7.(2016年山东)在[-1,1]上随机地取一个数k,则事件“直线y=kx与圆(x-5)2+y2=9相交”发生的概率为________.8.如图X952,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,则△AOC为钝角三角形的概率为________.图X9529.(2016年山东潍坊一模)甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图X953所示的圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.乙商场:从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖,问:购买该商品的顾客在哪家商场中奖的可能性大?图X953110.设事件A表示“关于x的方程x2+2ax+b2=0有实数根”.(1)若a,b∈{1,2,3},求事件A发生的概率P(A);(2)若a,b∈[1,3],求事件A发生的概率P(A).2第5讲几何概型1.C解析:令f(x0)=-x0(x0-2)≥0,得0≤x0≤2,由几何概型的概率公式,得任取一点x0∈[-1,3],使得f(x0)≥0的概率为p==.故选C.2.C3.C解析:设两串彩灯同时通电后,第一次闪亮的时刻分别为x,y,则0≤x≤4,0≤y≤4,而事件A“它们第一次闪亮的时刻相差不超过2秒”,即|x-y|≤2,可行域如图D181所示的阴影部分.由几何概型概率公式得P(A)==.图D181图D1824.C解析:z=(x-1)+yi⇒|z|=≤1⇒(x-1)2+y2≤1,如图D182可求得A(1,1),B(1,0),阴影面积等于π×12-×1×1=-.若|z|≤1,则y≥x的概率为=-.故选C.5.B解析:由已知,得B(1,0),C(1,2),D(-2,2),P(0,1),A(-2,10),则矩形ABCD的面积为3×2=6,阴影部分面积为×3×1=.故该点取自阴影部分的概率等于=.6.C解析:先求点P到点O的距离小于或等于1的概率,圆柱的体积V圆柱=π×12×2=2π,以O为球心,1为半径且在圆柱内部的半球的体积V半球=×π×13=π,则点P到点O的距离小于或等于1的概率为=,故点P到点O的距离大于1的概率为1-=.故选C.7.解析:直线y=kx与圆(x-5)2+y2=9相交,需要满足圆心到直线的距离小于半径,即d=<3.解得-