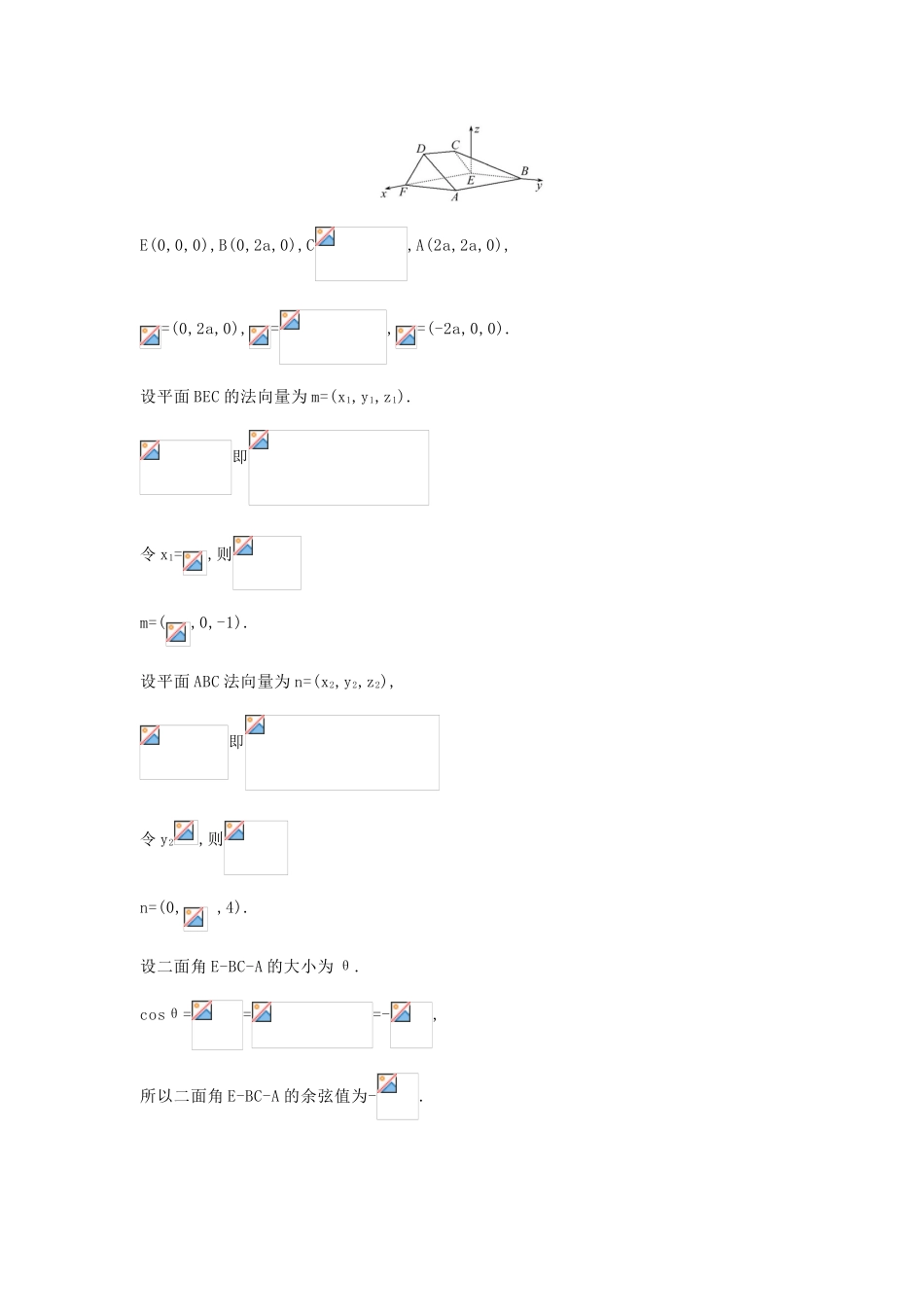
考点30立体几何中的向量方法一、解答题1.(2016·全国卷Ⅰ高考理科·T18)如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.(1)证明:平面ABEF⊥平面EFDC.(2)求二面角E-BC-A的余弦值.【解析】(1)因为ABEF为正方形,所以AF⊥EF.因为∠AFD=90°,所以AF⊥DF.因为DF∩EF=F,所以AF⊥面EFDC,AF⊂面ABEF,所以平面ABEF⊥平面EFDC.(2)由(1)知∠DFE=∠CEF=60°.因为AB∥EF,AB⊄平面EFDC,EF⊂平面EFDC,所以EF∥平面ABCD,AB⊂平面ABCD.因为面ABCD∩面EFDC=CD,所以AB∥CD,所以CD∥EF,所以四边形EFDC为等腰梯形,以E为原点,如图建立坐标系,设FD=a,E(0,0,0),B(0,2a,0),C,A(2a,2a,0),=(0,2a,0),=,=(-2a,0,0).设平面BEC的法向量为m=(x1,y1,z1).即令x1=,则m=(,0,-1).设平面ABC法向量为n=(x2,y2,z2),即令y2,则n=(0,,4).设二面角E-BC-A的大小为θ.cosθ===-,所以二面角E-BC-A的余弦值为-.2.(2016·全国卷Ⅱ理科·T19)如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=,EF交BD于点H.将△DEF沿EF折到△D'EF的位置,OD'=.(1)证明:D'H⊥平面ABCD.(2)求二面角B-D'A-C的正弦值.【解题指南】这是一道折叠问题,注意图形折叠前后变化和不变化的量.(1)要证线面垂直,只需证线线垂直.易证EF⊥HD',只需证明OH⊥HD',利用勾股定理证明即可.(2)由(1)知,D'H⊥平面ABCD,可建立空间直角坐标系求二面角的正弦值.【解析】(1)因为AE=CF=,所以,所以EF∥AC.因为四边形ABCD为菱形,所以AC⊥BD,所以EF⊥BD,所以EF⊥DH,所以EF⊥D'H.因为AC=6,所以AO=3;又AB=5,AO⊥OB,所以OB=4,所以OH=·OD=1,所以DH=D'H=3,所以|OD'|2=|OH|2+|D'H|2,所以D'H⊥OH.又因为OH∩EF=H,所以D'H⊥平面ABCD.(2)建立如图所示的坐标系,设二面角B-D'A-C的平面角为θ.B(5,0,0),C(1,3,0),D'(0,0,3),A(1,-3,0),=(4,3,0),=(-1,3,3),=(0,6,0),设平面ABD'的法向量为n1=(x,y,z),由得取所以n1=(3,-4,5).设平面ACD'的法向量为n2=(a,b,c),由得取所以n2=(3,0,1),所以|cosθ|=,所以sinθ=.3.(2016·全国卷Ⅲ·理科·T19)(本小题满分12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面PAB.(2)求直线AN与平面PMN所成角的正弦值.【解析】(1)由已知得AM=AD=2,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.又AD∥BC,故TN∥AM,TN=AM,四边形AMNT为平行四边形,于是MN∥AT.因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.(2)取BC的中点F,连接AF.由AB=AC得AF⊥BC,从而AF⊥AD且AF=,以A为坐标原点,的方向为x轴的正方向,的方向为y轴的正方向,的方向为z轴的正方向,建立空间直角坐标系,由题意可得P,M,C,N,所以,,,设n=(x,y,z)为平面PMN的法向量,则即可取n=,所以cos=.(3)因为AH=HF,所以,设H,所以,得:即H,所以,.所以直线BH和平面CEF所成角的正弦值为.