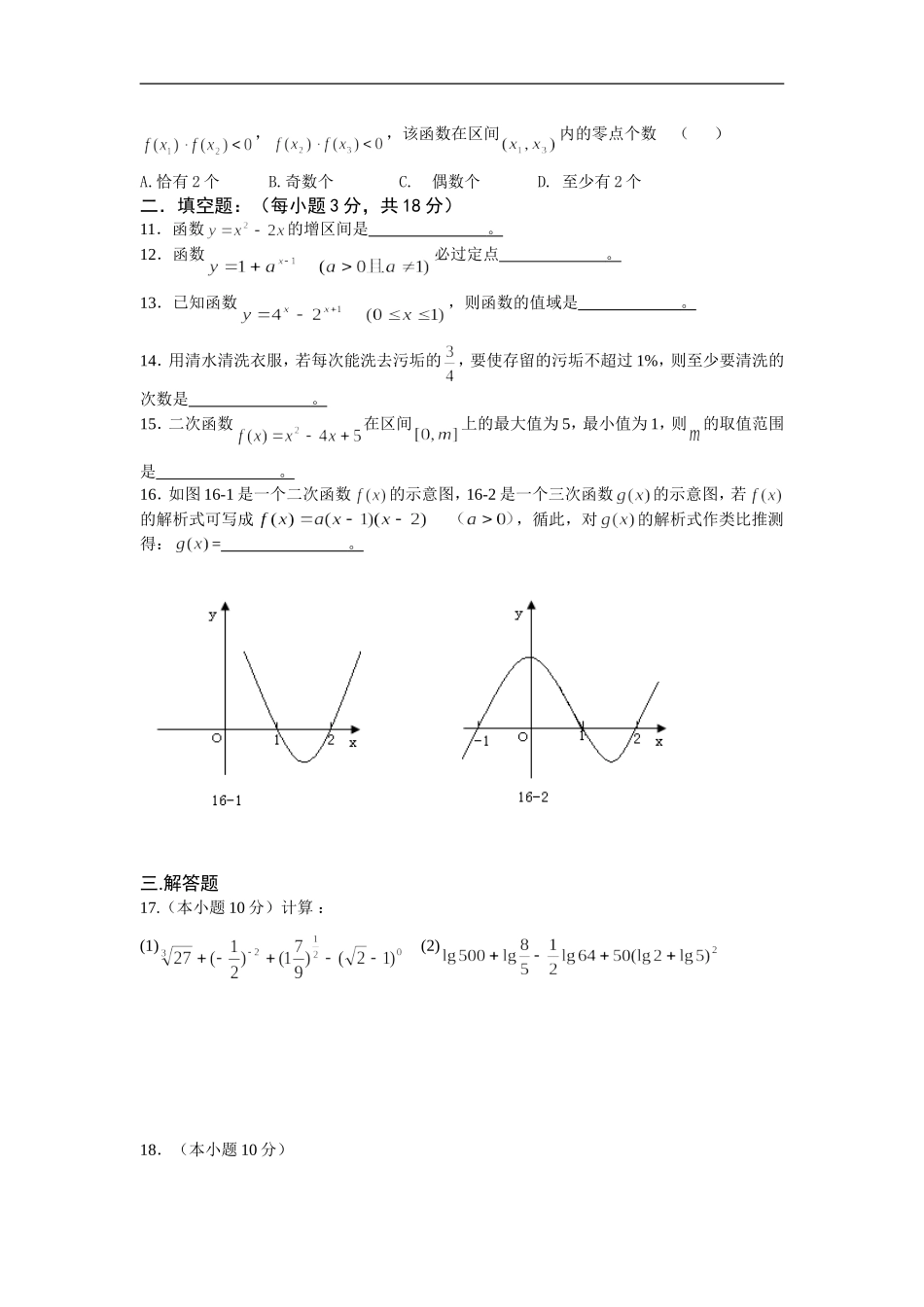
杭州高级中学2007学年第一学期高一期中考试数学试题一.选择题:(每小题3分,共30分)1.已知集合,则等于()A.B.C.D.2.下表表示是的函数,则该函数的值域是()01234A.B.C.D.3.设,从到的映射是“求正弦”,则中元素相对应的中元素应是()A.B.C.D.4.设,使幂函数的定义域为且为奇函数的所有的值是()A.B.C.D.5.设,,,则的大小关系是()A.B.C.D.6.函数是的增函数,则的取值范围是()A.B.C.D.7.已知是定义在上的增函数,且成立,则实数的取值范围是()A.B.C.D.8.设,函数在区间上的最大值与最小值之差为,则=()A.B.C.D.9.函数与在同一坐标系下的图象大致是()10.定义在上的函数,其图象是一条连续不断的曲线,设,且,,该函数在区间内的零点个数()A.恰有2个B.奇数个C.偶数个D.至少有2个二.填空题:(每小题3分,共18分)11.函数的增区间是。12.函数必过定点。13.已知函数,则函数的值域是。14.用清水清洗衣服,若每次能洗去污垢的,要使存留的污垢不超过1%,则至少要清洗的次数是。15.二次函数在区间上的最大值为5,最小值为1,则的取值范围是。16.如图16-1是一个二次函数的示意图,16-2是一个三次函数的示意图,若的解析式可写成,循此,对的解析式作类比推测得:=。三.解答题17.(本小题10分)计算:(1)(2)18.(本小题10分)已知全集,,,而且,,(1)求p+q的值(2)求19.(本小题10分)某学习小组对函数进行单调性及最值研究,先作以下数值估计:x-2-1.5-1-0.5-0.3-0.100.10.30.511.52y-0.4-0.461-0.5-0.4-0.275-0.09900.0990.2750.40.50.4610.4观察上表中随值变化的特点,完成以下问题:(1)函数在区间上递增,在区间及上递减,且在上的最小值与最大值之和;(2)用定义证明函数在区间上递增。20.(本小题10分)已知函数(1)求定义域并判断奇偶性;(2)求证;(3)若,求。21.(本小题10分)某种商品在30天内的销售价格P(元)与时间t天的函数关系用图甲表示,该商品在30天内日销售量Q(件)与时间t天之间的关系如下表所示:(1)根据所提供的图象(图甲)写出该商品每件的销售价格P与时间t的函数关系式;(2)在所给的直角坐标系(图乙)中,根据表中所提供的数据及描出的散点图,确定一个日销售量Q与时间t的函数关系式;(3)求该商品的日销售金额的最大值,并指出日销售金额的最大的一天是30天中的第几天?(日销售金额=每件的销售价格×日销售量)t(天)5152030Q(件)35252010春晖中学2007学年第一学期高一期中考试数学答卷二.填空题:(每小题3分,共18分)11.12.13.14.班级_______________姓名考号__________学号15.16.三.解答题17.(本小题10分)计算:(1)解:(2)解:18.(本小题10分)解:19.(本小题10分)解:(1)函数在区间上递增,在区间及上递减,且在上的最小值与最大值之和;(2)证明:20.(本小题10分)解:班级__________姓名___________考号__________学号21.(本小题12分)解: