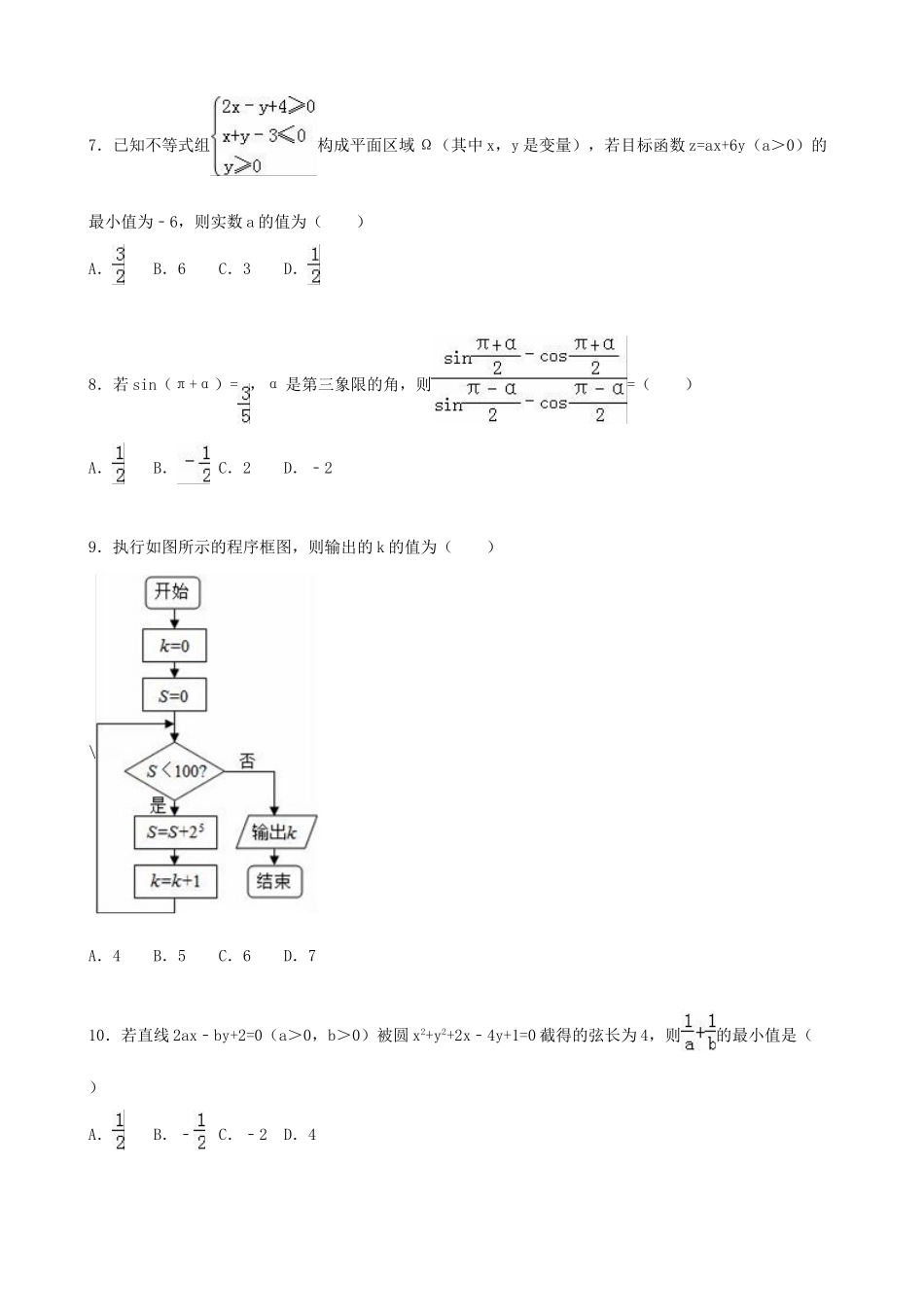
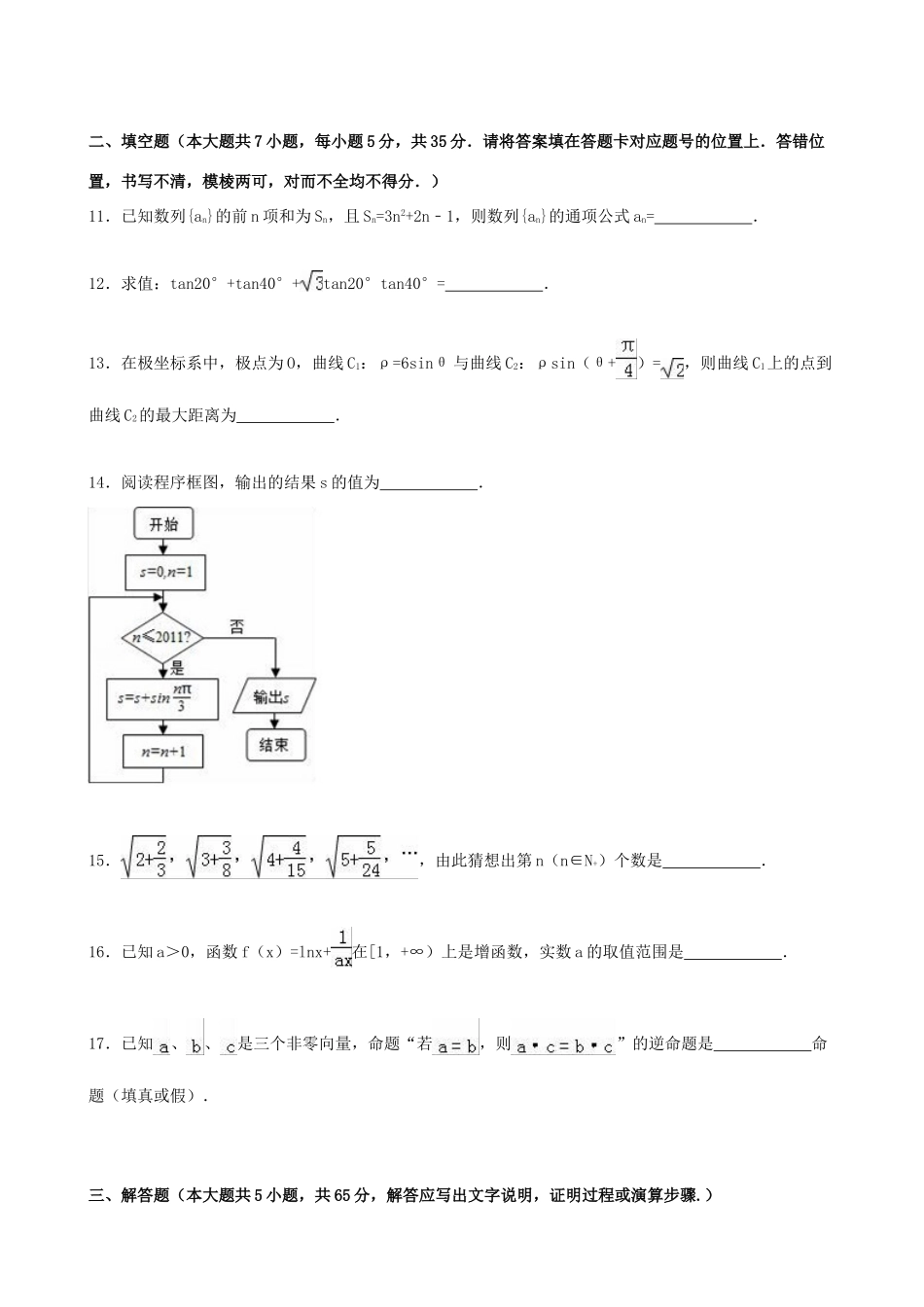
2015-2016学年湖北省襄阳市枣阳市白水高中高三(上)8月月考数学试卷(理科)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.不等式组的解集为()A.(0,)B.(,2)C.(,4)D.(2,4)2.已知全集U=R,A={x|x≤0},B={x|x>﹣1},则集合∁U(A∩B)=()A.{x|﹣1<x≤0}B.{x|﹣1≤x≤0}C.{x|x≤﹣1或x≥0}D.{x|x≤﹣1或x>0}3.已知函数f(x)=,若存在x1,x2,当0≤x1<4≤x2≤6时,f(x1)=f(x2),则x1•f(x2)的取值范围是()A.[0,1)B.[1,4]C.[1,6]D.[0,1]∪[3,8]4.已知双曲线的离心率为,则双曲线的渐近线方程为()A.B.C.y=±2xD.5.已知向量=(λ,1),=(λ+2,1),若|+|=|﹣|,则实数λ的值为()A.1B.2C.﹣1D.﹣26.已知函数,若,则f(﹣a)=()A.B.C.D.7.已知不等式组构成平面区域Ω(其中x,y是变量),若目标函数z=ax+6y(a>0)的最小值为﹣6,则实数a的值为()A.B.6C.3D.8.若sin(π+α)=,α是第三象限的角,则=()A.B.C.2D.﹣29.执行如图所示的程序框图,则输出的k的值为()\A.4B.5C.6D.710.若直线2ax﹣by+2=0(a>0,b>0)被圆x2+y2+2x﹣4y+1=0截得的弦长为4,则的最小值是()A.B.﹣C.﹣2D.4二、填空题(本大题共7小题,每小题5分,共35分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可,对而不全均不得分.)11.已知数列{an}的前n项和为Sn,且Sn=3n2+2n﹣1,则数列{an}的通项公式an=.12.求值:tan20°+tan40°+tan20°tan40°=.13.在极坐标系中,极点为O,曲线C1:ρ=6sinθ与曲线C2:ρsin(θ+)=,则曲线C1上的点到曲线C2的最大距离为.14.阅读程序框图,输出的结果s的值为.15.,由此猜想出第n(n∈N+)个数是.16.已知a>0,函数f(x)=lnx+在[1,+∞)上是增函数,实数a的取值范围是.17.已知、、是三个非零向量,命题“若,则”的逆命题是命题(填真或假).三、解答题(本大题共5小题,共65分,解答应写出文字说明,证明过程或演算步骤.)18.为了了解某市居民的用水量,通过抽样获得了100位居民的月均用水量图是调查结果的频率直方图.(1)估计该样本的平均数和中位数;(结果精确到0.01);(2)由(1)中结果估算该市12万居民的月均用水总量.19.已知函数为常数),数列{an}满足:,an+1=f(an),n∈N*.(1)当α=1时,求数列{an}的通项公式;(2)在(1)的条件下,证明对∀n∈N*有:;(3)若α=2,且对∀n∈N*,有0<an<1,证明:.20.平面内给定三个向量(1)求满足的实数m、n;(2)设满足且,求.21.设函数.(1)求f(x)在上的值域.(2)设A,B,C为△ABC的三个内角,若角C满足且边,求角A.22.在△ABC中,角A,B,C的对边分别是a,b,c,若acosC=csinA.(Ⅰ)求角C的大小;(Ⅱ)若a=3,△ABC的面积为,求的值.2015-2016学年湖北省襄阳市枣阳市白水高中高三(上)8月月考数学试卷(理科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.不等式组的解集为()A.(0,)B.(,2)C.(,4)D.(2,4)【考点】对数函数的单调性与特殊点;绝对值不等式.【专题】计算题;转化思想.【分析】不等式组化简为等价不等式组,分别求解取交集即可.【解答】解:不等式组可化为即:可得所以x∈(,4)故选C.【点评】本题考查对数函数的单调性与特殊点,绝对值不等式,考查计算能力,是基础题.2.已知全集U=R,A={x|x≤0},B={x|x>﹣1},则集合∁U(A∩B)=()A.{x|﹣1<x≤0}B.{x|﹣1≤x≤0}C.{x|x≤﹣1或x≥0}D.{x|x≤﹣1或x>0}【考点】交、并、补集的混合运算.【专题】集合.【分析】根据集合的基本运算进行求解即可.【解答】解: A={x|x≤0},B={x|x>﹣1},∴A∩B={x|﹣1<x≤0},则∁U(A∩B)={x|x≤﹣1或x>0},故选:D.【点评】本题主要考查集合关系的应用,比较基础.3.已知函数f(x)=,若存在x1,x2,当0≤x1<4≤x2≤6时,f(x1)=f(x2),则x1•f(x2)的...