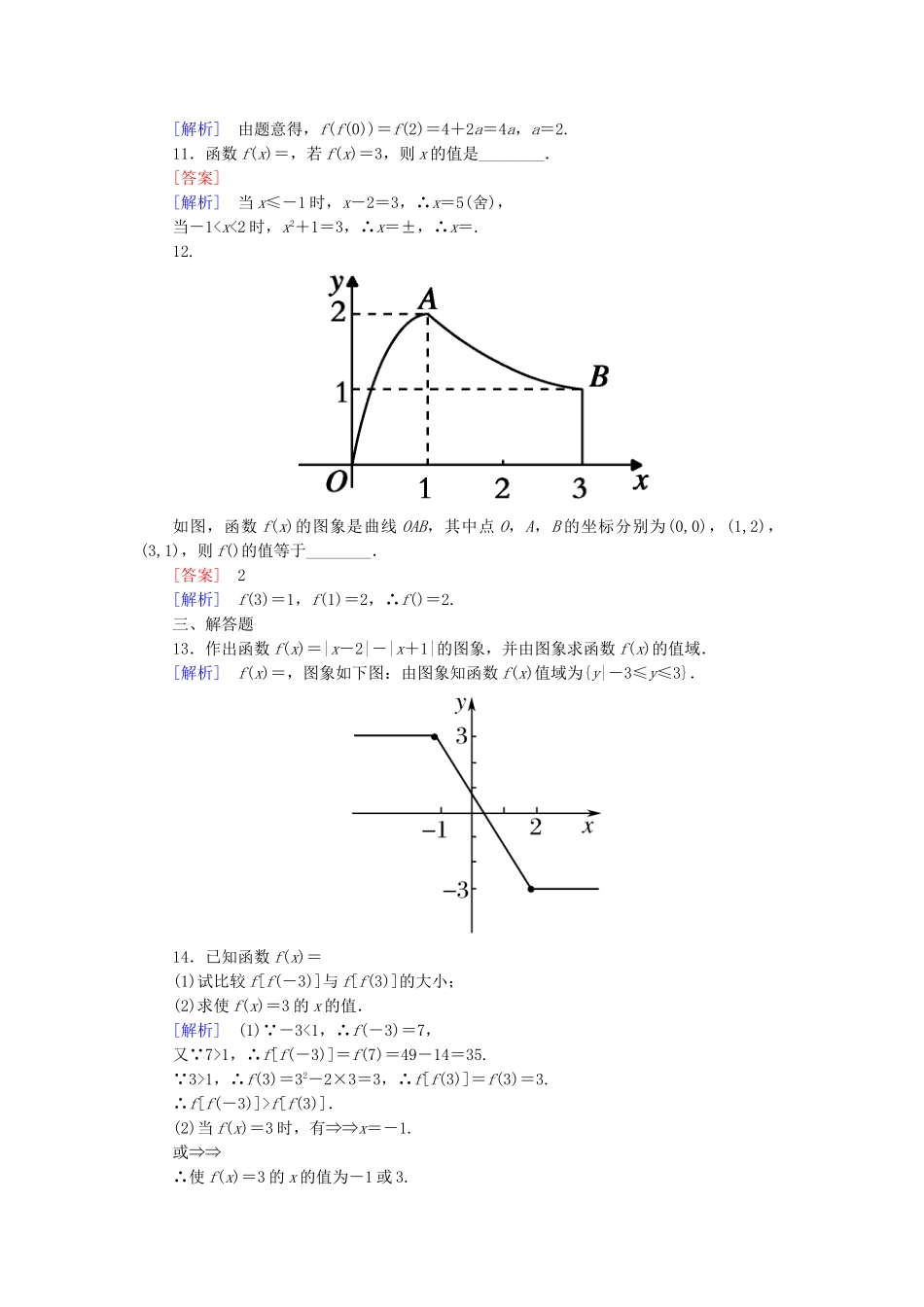
【成才之路】高中数学1-2-2-2分段函数与映射能力强化提升新人教A版必修1一、选择题1.给出下列四个命题:(1)若A={整数},B={正奇数},则一定不能建立从集合A到集合B的映射;(2)若A是无限集,B是有限集,则一定不能建立从集合A到集合B的映射;(3)若A={a},B={1,2},则从集合A到集合B只能建立一个映射;(4)若A={1,2},B={a},则从集合A到集合B只能建立一个映射.其中正确命题的个数是()A.0个B.1个C.2个D.3个[答案]B[解析]对于(1)f:A→B对应法则f:x→2|x|+1故(1)错;(2)f:R→{1},对应法则f:x→1,(2)错;(3)可以建立两个映射,(3)错;(4)正确,故选B.2.(~瓮安一中周测试题)下列从P到Q的各对应关系f中,不是映射的是()A.P=N,Q=N*,f:x→|x-8|B.P={1,2,3,4,5,6},Q={-4,-3,0,5,12},f:x→x(x-4)C.P=N*,Q={-1,1},f:x→(-1)xD.P=Z,Q={有理数},f:x→x2[答案]A[解析]对于选项A,当x=8时,|x-8|=0∉N*,∴不是映射,故选A.3.已知集合M={x|0≤x≤6},P={y|0≤y≤3},则下列对应关系中,不能看作从M到P的映射的是()A.f:x→y=xB.f:x→y=xC.f:x→y=xD.f:x→y=x[答案]C[解析]对于选项C,当x=6时,y=6,当6∉P,故选C.4.集合A={a,b,c},B={d,e}则从A到B可以建立不同的映射个数为()A.5B.6C.8D.9[答案]C[解析]用树状图写出所有的映射为:a→da→e共8个.5.已知f(x)=则f(f(f(-4)))=()A.-4B.4C.3D.-3[答案]B[解析]f(-4)=(-4)+4=0,∴f(f(-4))=f(0)=1,f(f(f(-4)))=f(1)=12+3=4.故选B.6.(~·潍坊一中月考试题)设函数f(x)=则f()的值为()A.B.-C.D.18[答案]A[解析]f(2)=4,=,故f()=f()=1-()2=.7.(河南高中~高一第一次考试)已知映射f:A→B,其中A=B=R,对应为f:x→y=x2-2x+2,若对实数k∈B,在集合中没有元素对应,则k的取值范围是()A.(-∞,1]B.(-∞,1)C.(1,+∞)D.[1,+∞)[答案]B[解析]设k=x2-2x+2即x2-2x+2-k=0,k没有元素对应即上述方程无解Δ<0,(-2)2-4(2-k)<0,∴k<1故选B.8.某市出租车起步价为5元(起步价内行驶里程为3km),以后每1km价为1.8元(不足1km按1km计价),则乘坐出租车的费用y(元)与行驶的里程x(km)之间的函数图象大致为下列图中的()[答案]B[解析]由已知得y==.故选B.二、填空题9.已知M={正整数},N={正奇数},映射f:a→b=2a-1,(a∈M,b∈N),则在映射f下M中的元素11对应N中的元素是________.[答案]21[解析]b=2×11-1=21.10.(~山东泗水一中月考试题)已知函数f(x)=若f(f(0))=4a,则实数a=________.[答案]2[解析]由题意得,f(f(0))=f(2)=4+2a=4a,a=2.11.函数f(x)=,若f(x)=3,则x的值是________.[答案][解析]当x≤-1时,x-2=3,∴x=5(舍),当-11,∴f[f(-3)]=f(7)=49-14=35. 3>1,∴f(3)=32-2×3=3,∴f[f(3)]=f(3)=3.∴f[f(-3)]>f[f(3)].(2)当f(x)=3时,有⇒⇒x=-1.或⇒⇒∴使f(x)=3的x的值为-1或3.15.在国内投寄外埠平信,每封信不超过20g重付邮资80分,超过20g重而不超过40g重付邮资160分.试写出x(0≤x≤40)克重的信应付的邮资y(分)与x(g)的函数关系,并求函数的定义域,然后作出函数的图象.[解析]y=定义域为[0,40],图象如下16.如图所示,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B,C在x轴上,A、D在抛物线上矩形ABCD在抛物线与x轴所围成的图形内.(1)求二次函数解析式;(2)设A(x,y),试求矩形ABCD的周长P关于x的函数关系,并求x的取值范围;(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你...