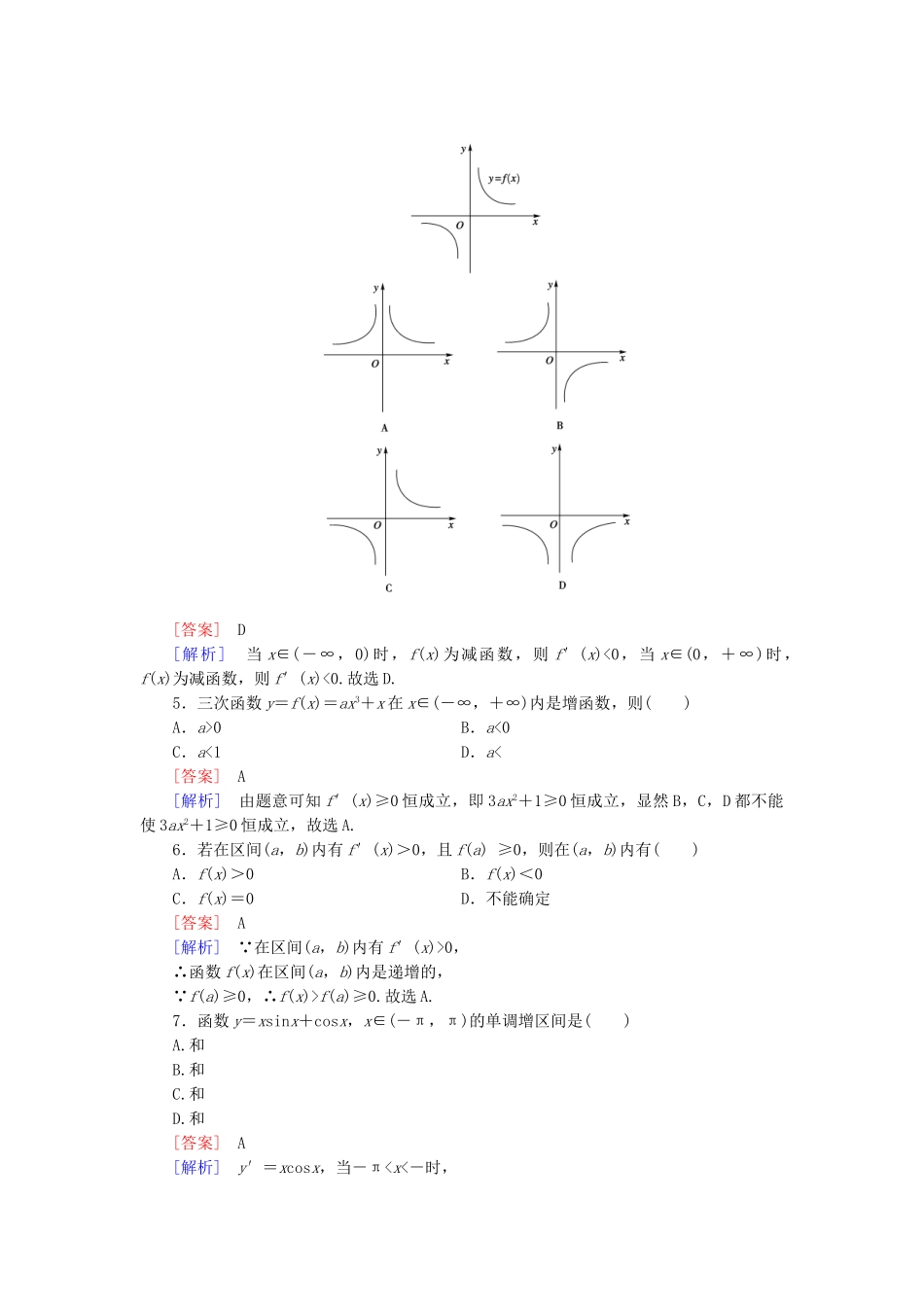
【成才之路】-学年高中数学1.3第1课时利用导数判断函数的单调性同步测试新人教B版选修2-2一、选择题1.函数y=x4-2x2+5的单调减区间为()A.(-∞,-1]和[0,1]B.[-1,0]和[1,+∞)C.[-1,1]D.(-∞,-1]和[1,+∞)[答案]A[解析]y′=4x3-4x,令y′=0,则4x3-4x=0,解x=0或x=±1,列表如下:x(-∞,-1)-1(-1,0)0(0,1)1(1,+∞)y′-+-+y故单调减区间为(-∞,-1]和[0,1].2.函数f(x)=2x-sinx()A.是增函数B.是减函数C.在(0,+∞)上增,在(-∞,0)上减D.在(0,+∞)上减,在(-∞,0)上增[答案]A[解析]f′(x)=2-cosx>0在(-∞,+∞)上恒成立.故选A.3.函数y=xlnx在区间(0,1)上是()A.单调增函数B.单调减函数C.在上是减函数,在上是增函数D.在上是增函数,在上是减函数[答案]C[解析]f′(x)=lnx+1,当00.∴函数在上是减函数,在上是增函数.4.函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是()[答案]D[解析]当x∈(-∞,0)时,f(x)为减函数,则f′(x)<0,当x∈(0,+∞)时,f(x)为减函数,则f′(x)<0.故选D.5.三次函数y=f(x)=ax3+x在x∈(-∞,+∞)内是增函数,则()A.a>0B.a<0C.a<1D.a<[答案]A[解析]由题意可知f′(x)≥0恒成立,即3ax2+1≥0恒成立,显然B,C,D都不能使3ax2+1≥0恒成立,故选A.6.若在区间(a,b)内有f′(x)>0,且f(a)≥0,则在(a,b)内有()A.f(x)>0B.f(x)<0C.f(x)=0D.不能确定[答案]A[解析] 在区间(a,b)内有f′(x)>0,∴函数f(x)在区间(a,b)内是递增的, f(a)≥0,∴f(x)>f(a)≥0.故选A.7.函数y=xsinx+cosx,x∈(-π,π)的单调增区间是()A.和B.和C.和D.和[答案]A[解析]y′=xcosx,当-π0,当00,∴y′=xcosx>0.故选A.8.(·福建省闽侯二中、永泰二中、连江侨中、长乐二中联考)设函数F(x)=是定义在R上的函数,其中f(x)的导函数f′(x)满足f′(x)e2f(0),f()>ef(0)B.f(2)ef(0)C.f(2)e2f(0),f()1在区间(1,+∞)内恒成立,则实数a的取值范围为________.[答案]a≥1[解析]由f(x)>1得ax-lnx-1>0,即a>在(1,+∞)上恒成立.设g(x)=,g′(x)=-. x>1,∴g′(x)<0,∴g(x)单调递减.所以g(x)0得-.∴增区间为;减区间为,.(2)y′=3x2-18x+24=3(x-2)(x-4),由y′>0得x<2或x>4;由y′<0得2