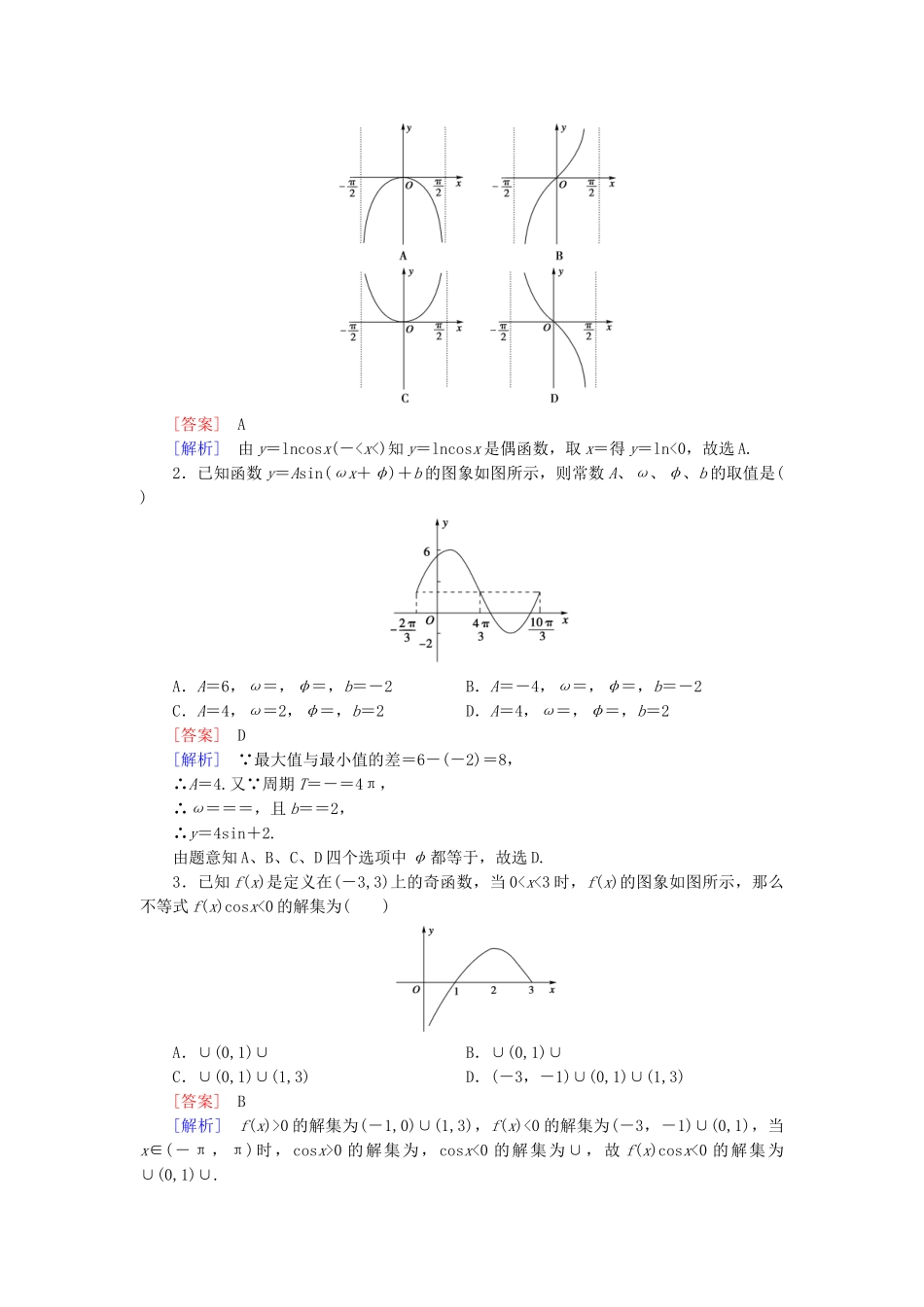
【成才之路】-学年高中数学1.3.2第1课时余弦函数的图象与性质基础巩固新人教B版必修4一、选择题1.函数y=|cosx|的周期为()A.2πB.πC.D.[答案]B[解析]作出函数y=|cosx|的简图,由图象可知,函数y=|cosx|的周期为π.2.(·浙江临海市杜桥中学高一月考)要得到函数g(x)=cosx的图象,只需将f(x)=cos(x-)的图象()A.向右平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向左平移个单位长度[答案]D[解析]将f(x)=cos(x-)的图象向左平移个单位长度得到g(x)=cos[(x+)-]=cosx,故选D.3.(·山东济南一中高一月考)函数y=cos2x的图象()A.关于直线x=-对称B.关于直线x=-对称C.关于直线x=对称D.关于直线x=对称[答案]B[解析]令2x=kπ(k∈Z),则x=,k∈Z.当k=-1时,x=-,故选B.4.已知函数y=cos(ωx+φ)在一个周期内如图所示.设其周期为T,则有()A.T=,φ=B.T=,φ=C.T=3π,φ=-D.T=3π,φ=[答案]A[解析]=-==,T=.5.要得到函数y=cos(2x+1)的图象,只要将函数y=cos2x的图象()A.向左平移1个单位B.向右平移1个单位C.向左平移个单位D.向右平移个单位[答案]C[解析]本题考查三角函数(余弦型函数)图象的平移问题. y=cos(2x+1)=cos2(x+),所以只须将y=cos2x图象向左平移个单位即可得到y=cos(2x+1)的图象.注意图象平移是对“x”而言的.6.设f(x)是定义域为R,最小正周期为的函数,若f(x)=,则f的值等于()A.1B.C.0D.-【答案】B【解析】f=f=f=sin=.二、填空题7.函数y=的定义域为________.[答案](-+2kπ,+2kπ](k∈Z)[解析]由已知得,,结合正、余弦函数图象可知,-+2kπ0时,-b≤-bcosx≤b,∴a-b≤a-bcosx≤a+b.∴,解得.∴y=-4bsinax=-4sinx,最大值为4,最小值为-4,最小正周期为4π.当b<0时,b≤-bcosx≤-b,∴a+b≤a-bcosx≤a-b.∴,解得.∴y=-4bsinax=4sinx,最大值为4,最小值为-4,最小正周期为4π.一、选择题1.函数y=lncosx(-0的解集为(-1,0)∪(1,3),f(x)<0的解集为(-3,-1)∪(0,1),当x∈(-π,π)时,cosx>0的解集为,cosx<0的解集为∪,故f(x)cosx<0的解集为∪(0,1)∪.4.把函数y=cos的图象向右平移φ个单位,所得到的函数图象正好关于y轴对称,则φ的最小值为()A.B.C.D.[答案]C[解析]当φ=时,得y=cos=cos(π+x)=-cosx,所以图象关于y轴对称.二、填空题5.已知f(n)=cos,n∈N*,则f(1)+f(2)+f(3)+…+f(100)=________.[答案]-1[解析]因f(n)=cos的周期T=8,且f(1)+f(2)+…+f(8)=0.所以f(1)+f(2)+…+f(100)=f(1)+f(2)+f(3)+f(4)=cos+cos+cos+cosπ=-1.6.已知函数y=Asin(ωx+φ),在同一周期内当x=时,ymax=2;当x=时,ymin=-2,那么函数的解析式为________.[答案]y=2sin[解析] =-=,∴T=π,ω=2,又A=2,∴y=2sin(2x+φ)过点,∴sin=1,∴φ=+2kπ(k∈Z).三、解答...