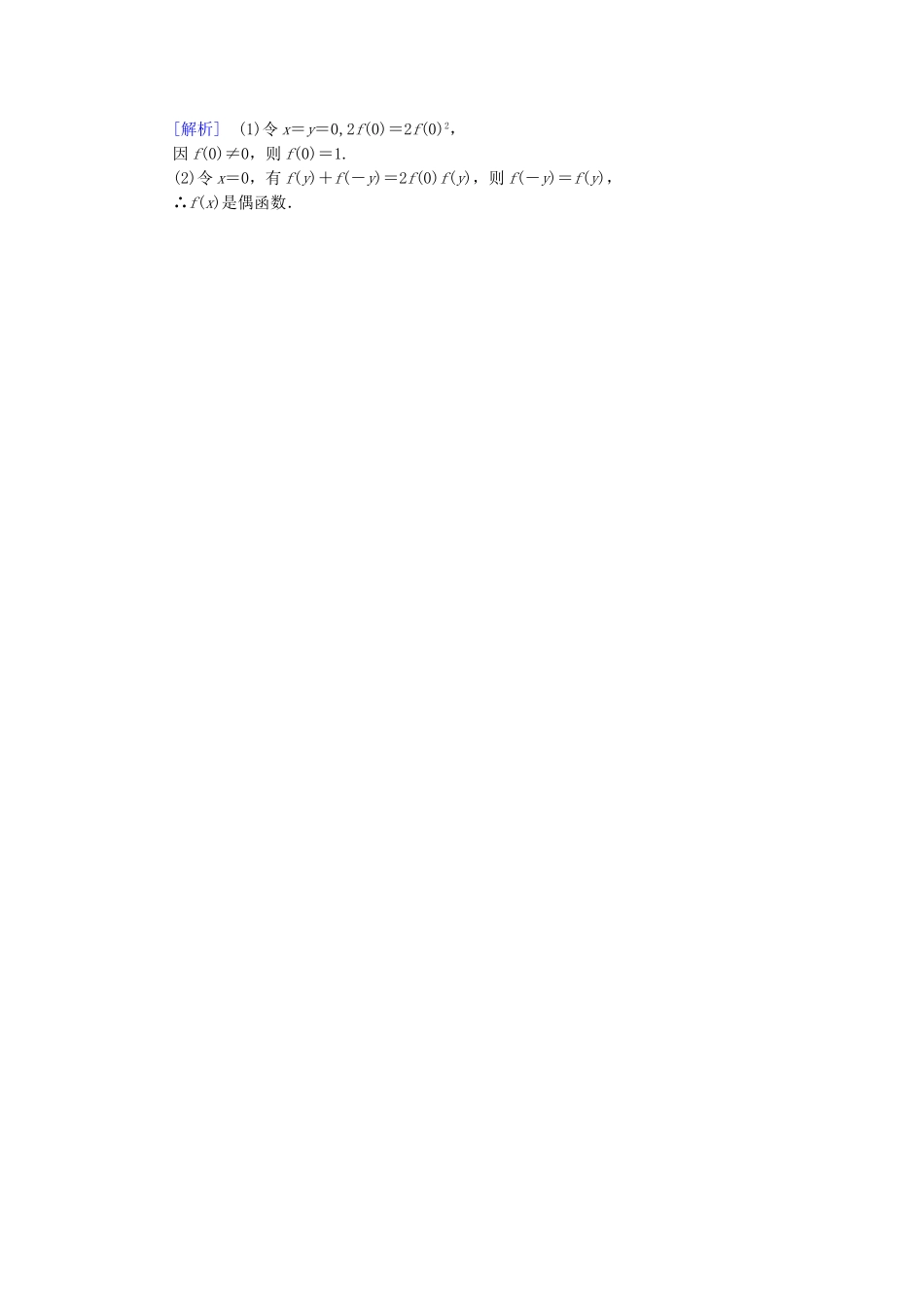
【成才之路】-学年高中数学1.3.2奇偶性第1课时函数的奇偶性课后强化作业新人教A版必修1一、选择题1.下列图象表示的函数具有奇偶性的是()[答案]B2.下列命题中错误的是()①图象关于原点成中心对称的函数一定为奇函数;②奇函数的图象一定过原点;③偶函数的图象与y轴一定相交;④图象关于y轴对称的函数一定为偶函数.A.①②B.③④C.①④D.②③[答案]D[解析]f(x)=为奇函数,其图象不过原点,故②错;y=为偶函数,其图象与y轴不相交,故③错.3.(~山东冠县武训中学月考试题)下列函数中是偶函数的是()A.y=x4-3B.y=x2x∈(-3,3]C.y=-D.y=2(x-1)2+1[答案]A4.若f(x)=ax2+bx+c(c≠0)是偶函数,则g(x)=ax3+bx2+cx()A.是奇函数但不是偶函数B.是偶函数但不是奇函数C.既是奇函数又是偶函数D.既非奇函数又非偶函数[答案]A[解析]∵f(-x)=f(x),∴a(-x)2-bx+c=ax2+bx+c对x∈R恒成立.∴b=0.∴g(x)=ax3+cx.∴g(-x)=-g(x).5.已知f(x)=x7+ax5+bx-5,且f(-3)=5,则f(3)=()A.-15B.15C.10D.-10[答案]A[解析]解法1:f(-3)=(-3)7+a(-3)5+(-3)b-5=-(37+a·35+3b-5)-10=-f(3)-10=5,∴f(3)=-15.解法2:设g(x)=x7+ax5+bx,则g(x)为奇函数,∵f(-3)=g(-3)-5=-g(3)-5=5,∴g(3)=-10,∴f(3)=g(3)-5=-15.6.(·辽宁)若函数f(x)=为奇函数,则a=()A.B.C.D.1[答案]A[分析]因为已知函数为奇函数,所以其定义域应关于原点对称,由此求a.[解析]要使函数式有意义,则x≠-,x≠a,而函数为奇函数,所以其定义域应关于原点对称,由此得a=.经验证当a=时,函数f(x)是奇函数.二、填空题7.若函数f(x)是奇函数,则f(1+)+f()=________.[答案]0[解析]=-(1+),∴f(1+)+f()=f(1+)-f(1+)=0.8.已知f(x)为奇函数,g(x)=f(x)+9,g(-2)=3,则f(2)=________.[答案]6[分析]将x=-2代入g(x)=f(x)+9,利用f(-2)=-f(2)求f(2).[解析]根据已知条件,得g(-2)=f(-2)+9,又f(x)为奇函数,所以f(-2)=-f(2),则3=-f(2)+9,即f(2)=6.9.(~河南安阳一中月考试题)若函数f(x)=(x+a)(bx+2a)(常数a,b)是偶函数,它的值域为(-∞,4],则该函数的解析式f(x)=________.[答案]-2x2+4[解析]由于f(x)=(x+a)(bx+2a)=bx2+(ab+2a)x+2a2,所以f(-x)=bx2-(ab+2a)x+2a2,∴ab+2a=0,∴a=0或b=-2.又f(x)最大值4.所以b=-2,且f(0)=2a2=4,∴a=±,∴f(x)=-2x2+4.三、解答题10.函数f(x)=是定义在(-1,1)上的奇函数,且f=,求函数f(x)的解析式.[解析]因为f(x)是奇函数且定义域为(-1,1),所以f(0)=0,即b=0.又f=,所以=,所以a=1,所以f(x)=.11.已知f(x)是偶函数,g(x)是奇函数,且f(x)+g(x)=x2+x-2,求f(x),g(x)的表达式.[解析]f(-x)+g(-x)=x2-x-2,由f(x)是偶函数,g(x)是奇函数得,f(x)-g(x)=x2-x-2又f(x)+g(x)=x2+x-2,两式联立得:f(x)=x2-2,g(x)=x.12.已知f(x)是定义在R上的函数,对任意的x,y∈R都有f(x+y)+f(x-y)=2f(x)f(y),且f(0)≠0.(1)求证:f(0)=1.(2)判断函数的奇偶性.[解析](1)令x=y=0,2f(0)=2f(0)2,因f(0)≠0,则f(0)=1.(2)令x=0,有f(y)+f(-y)=2f(0)f(y),则f(-y)=f(y),∴f(x)是偶函数.