高中数学 3-2-3 直线方程的一般式能力强化提升 新人教A版必修2VIP免费

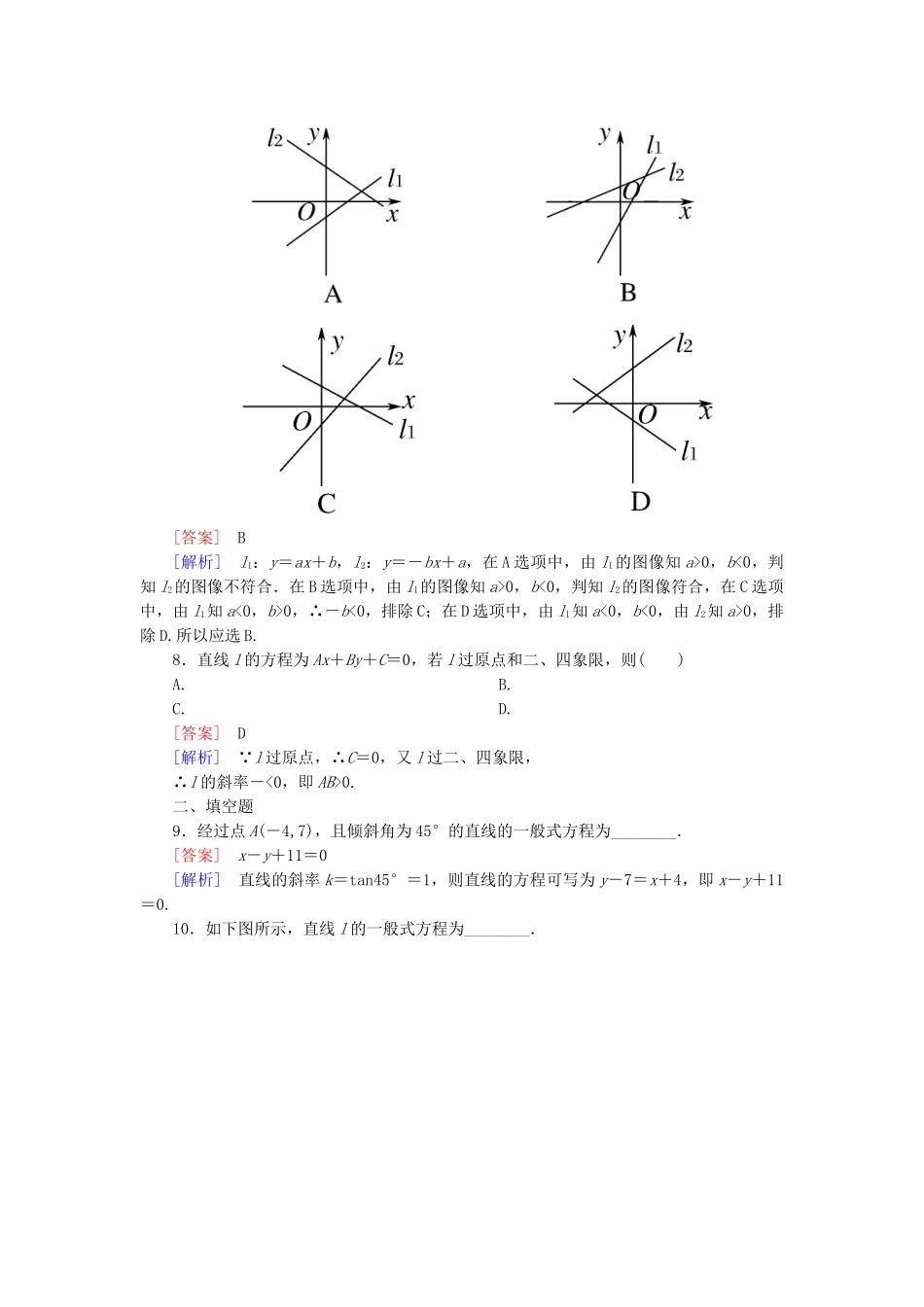
【成才之路】高中数学3-2-3直线方程的一般式能力强化提升新人教A版必修2一、选择题1．在x轴与y轴上的截距分别是－2与3的直线方程是()A．2x－3y－6＝0B．3x－2y－6＝0C．3x－2y＋6＝0D．2x－3y＋6＝0[答案]C[解析]因为直线在x轴，y轴上的截距分别为－2,3，由直线方程的截距式得直线方程为＋＝1，即3x－2y＋6＝0.2．若直线l的一般式方程为2x－y＋1＝0，则直线l不经过()A．第一象限B．第二象限C．第三象限D．第四象限[答案]D3．下列各组中的两条直线平行的有()(1)2x＋y－11＝0，x＋3y－18＝0(2)2x－3y－4＝0,4x－6y－8＝0(3)3x－4y－7＝0,12x－16y－7＝0A．0组B．1组C．2组D．3组[答案]B[解析]第一组相交，第二组重合，第三组平行，故选B.4．若直线x＋2ay－1＝0与(a－1)x－ay＋1＝0平行，则a的值为()A.B.或0C．0D．－2[答案]B[解析]由已知得1×(－a)－2a(a－1)＝0，即2a2－a＝0，解得a＝0或，故选B.5．直线(3－a)x＋(2a－1)y＋7＝0与直线(2a＋1)x＋(a＋5)y－6＝0互相垂直，则a值是()A．－B.C.D.[答案]B[解析]由(3－a)(2a＋1)＋(2a－1)(a＋5)＝0得a＝.6．直线l过点(－1,2)且与直线2x－3y＋4＝0垂直，则l的方程是()A．3x＋2y－1＝0B．3x＋2y＋7＝0C．2x－3y＋5＝0D．2x－3y＋8＝0[答案]A[解析]由直线l与直线2x－3y＋4＝0垂直，可知直线l的斜率是－，由点斜式可得直线l的方程为y－2＝－(x＋1)，即3x＋2y－1＝0.7．直线l1ax－y＋b＝0，l2bx＋y－a＝0(ab≠0)的图像只可能是下图中的()[答案]B[解析]l1：y＝ax＋b，l2：y＝－bx＋a，在A选项中，由l1的图像知a>0，b<0，判知l2的图像不符合．在B选项中，由l1的图像知a>0，b<0，判知l2的图像符合，在C选项中，由l1知a<0，b>0，∴－b<0，排除C；在D选项中，由l1知a<0，b<0，由l2知a>0，排除D.所以应选B.8．直线l的方程为Ax＋By＋C＝0，若l过原点和二、四象限，则()A.B.C.D.[答案]D[解析] l过原点，∴C＝0，又l过二、四象限，∴l的斜率－<0，即AB>0.二、填空题9．经过点A(－4,7)，且倾斜角为45°的直线的一般式方程为________．[答案]x－y＋11＝0[解析]直线的斜率k＝tan45°＝1，则直线的方程可写为y－7＝x＋4，即x－y＋11＝0.10．如下图所示，直线l的一般式方程为________．[答案]2x＋y＋2＝0[解析]由图知，直线l在x轴，y轴上的截距分别为－1，－2，则直线l的截距式方程为＋＝1，即2x＋y＋2＝0.11．若直线(a＋2)x＋(a2－2a－3)y－2a＝0在x轴上的截距为3，则实数a的值为________．[答案]－6[解析]把x＝3，y＝0代入方程(a＋2)x＋(a2－2a－3)y－2a＝0中得3(a＋2)－2a＝0，a＝－6.12．已知直线的斜率为，且和坐标轴围成面积为3的三角形，该直线的方程为________．[答案]x－6y＋6＝0或x－6y－6＝0[解析]设直线的方程为＋＝1， 直线的斜率k＝，∴－＝，又 |ab|＝3，∴或∴所求直线方程为：x－6y＋6＝0或x－6y－6＝0.三、解答题13．把直线l的一般式方程2x－3y－6＝0化成斜截式，求出直线l的斜率以及它在x轴与y轴上的截距，并画出图形．[分析]求l在x轴上的截距，即求直线l与x轴交点的横坐标．在l的方程中令y＝0，解出x值，即为x轴上的截距，令x＝0，解出y值，即为y轴上的截距．[解析]由2x－3y－6＝0得3y＝2x－6，∴y＝x－2，即直线l的一般式方程化成斜截式为y＝x－2，斜率为.在l的方程2x－3y－6＝0中，令y＝0，得x＝3；令x＝0，得y＝－2.即直线l在x轴与y轴上的截距分别是3，－2.则直线l与x轴，y轴交点分别为A(3,0)，B(0，－2)，过点A，B作直线，就得直线l的图形，如右图所示．[点评]已知一般式方程讨论直线的性质：①令x＝0，解得y值，即为直线在y轴上的截距，令y＝0，解得x值，即为直线在x轴上的截距，从而确定直线与两坐标轴的交点坐标，从而画出图形．当然也可将一般式方程化为截距式来解决；②化为斜截式可讨论斜率与倾斜角，以及在y轴上的截距．14．(1)已知三直线l12x－4y＋7＝0，l2x－2y＋5＝0，l34x＋2y－1＝0，求证：l1∥l2，l1⊥l3；(2)求过点A(2,2)且分别满足下列条件的直线方程：与直线l：3x＋4y－20＝0平行；与直线l：3x＋4y－20＝0垂直．[解析](1)把l1、l2、l3的方程写成斜截式得l1y＝x＋；l2y＝x＋；l3y＝－2x＋， ...