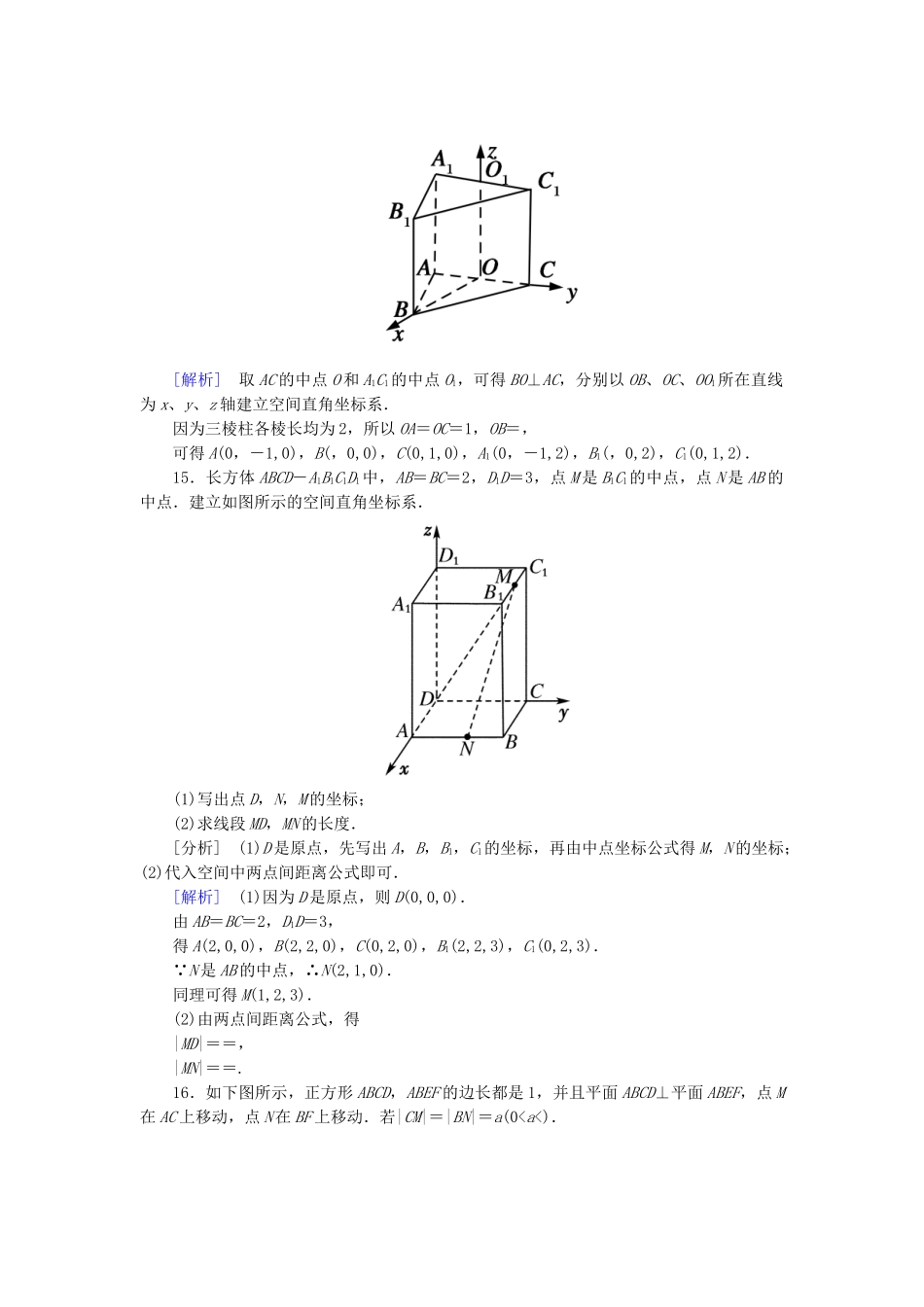
【成才之路】高中数学4-3-1、2空间直角坐标系空间两点间的距离公式能力强化提升新人教A版必修2一、选择题1.在空间直角坐标系中,在z轴上的点的坐标可记为()A.(0,b,0)B.(a,0,0)C.(0,0,c)D.(0,b,c)[答案]C2.已知点A(1,-3,4),则点A关于y轴的对称点的坐标为()A.(-1,-3,-4)B.(-4,1,-3)C.(3,-1,-4)D.(4,-1,3)[答案]A3.点P(-1,2,3)关于xOz平面对称的点的坐标是()A.(1,2,3)B.(-1,-2,3)C.(-1,2,-3)D.(1,-2,-3)[答案]B4.已知点A(-3,1,5)与点B(4,3,1),则AB的中点坐标是()A.(,1,-2)B.(,2,3)C.(-12,3,5)D.(,,2)[答案]B5.点P(0,1,4)位于()A.y轴上B.x轴上C.xOz平面内D.yOz平面内[答案]D[解析]由于点P的横坐标是0,则点P在yOz平面内.6.点A在z轴上,它到点(3,2,1)的距离是,则点A的坐标是()A.(0,0,-1)B.(0,1,1)C.(0,0,1)D.(0,0,13)[答案]C[解析]设A(0,0,c),则=,解得c=1.所以点A的坐标为(0,0,1).7.△ABC的顶点坐标是A(3,1,1),B(-5,2,1),C(-,2,3),则它在yOz平面上射影图形的面积是()A.4B.3C.2D.1[答案]D[解析]△ABC的顶点在yOz平面上的射影点的坐标分别为A′(0,1,1),B′(0,2,1),C′(0,2,3),△ABC在yOz平面上的射影是一个直角三角形A′B′C′,容易求出它的面积为1.8.空间直角坐标系中,点A(3,2,-5)到x轴的距离d等于()A.B.C.D.[答案]B[解析]过A作AB⊥x轴于B,则B(3,0,0),则点A到x轴的距离d=|AB|=.二、填空题9.点M(1,-4,3)关于点P(4,0,-3)的对称点M′的坐标是________.[答案](7,4,-9)[解析]线段MM′的中点是点P,则M′(7,4,-9).10.在空间直角坐标系中,点M的坐标是(4,5,6),则点M关于y轴的对称点在坐标平面xOz上的射影的坐标为________.[答案](-4,0,-6)[解析]点M关于y轴的对称点是M′(-4,5,-6),则点M′在坐标平面xOz上的射影是(-4,0,-6).11.在△ABC中,已知A(-1,2,3),B(2,-2,3),C(,,3),则AB边上的中线CD的长是________.[答案][解析]由题可知AB的中点D的坐标是D(,0,3),由距离公式可得|CD|==.12.在空间直角坐标系中,正方体ABCD—A1B1C1D1的顶点A(3,-1,2),其中心M的坐标为(0,1,2),则该正方体的棱长为________.[答案][解析]|AM|==,∴对角线|AC1|=2,设棱长x,则3x2=(2)2,∴x=.三、解答题13.已知点A(1,-2,11),B(4,2,3),C(6,-1,4),试判断△ABC的形状.[分析]求出三角形边长,利用三边的关系来判断其形状.[解析]由题意得:|AB|==,|BC|==,|AC|==.∵|BC|2+|AC|2=|AB|2,∴△ABC为直角三角形.14.如图,三棱柱ABC-A1B1C1中,所有棱长都为2,侧棱AA1⊥底面ABC,建立适当坐标系写出各顶点的坐标.[分析]题中给出了三棱柱的棱长,要求各顶点的坐标,可以作出两两垂直的三条线分别为x、y、z轴建立空间直角坐标系,然后确定各点坐标.[解析]取AC的中点O和A1C1的中点O1,可得BO⊥AC,分别以OB、OC、OO1所在直线为x、y、z轴建立空间直角坐标系.因为三棱柱各棱长均为2,所以OA=OC=1,OB=,可得A(0,-1,0),B(,0,0),C(0,1,0),A1(0,-1,2),B1(,0,2),C1(0,1,2).15.长方体ABCD-A1B1C1D1中,AB=BC=2,D1D=3,点M是B1C1的中点,点N是AB的中点.建立如图所示的空间直角坐标系.(1)写出点D,N,M的坐标;(2)求线段MD,MN的长度.[分析](1)D是原点,先写出A,B,B1,C1的坐标,再由中点坐标公式得M,N的坐标;(2)代入空间中两点间距离公式即可.[解析](1)因为D是原点,则D(0,0,0).由AB=BC=2,D1D=3,得A(2,0,0),B(2,2,0),C(0,2,0),B1(2,2,3),C1(0,2,3).∵N是AB的中点,∴N(2,1,0).同理可得M(1,2,3).(2)由两点间距离公式,得|MD|==,|MN|==.16.如下图所示,正方形ABCD,ABEF的边长都是1,并且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动.若|CM|=|BN|=a(0