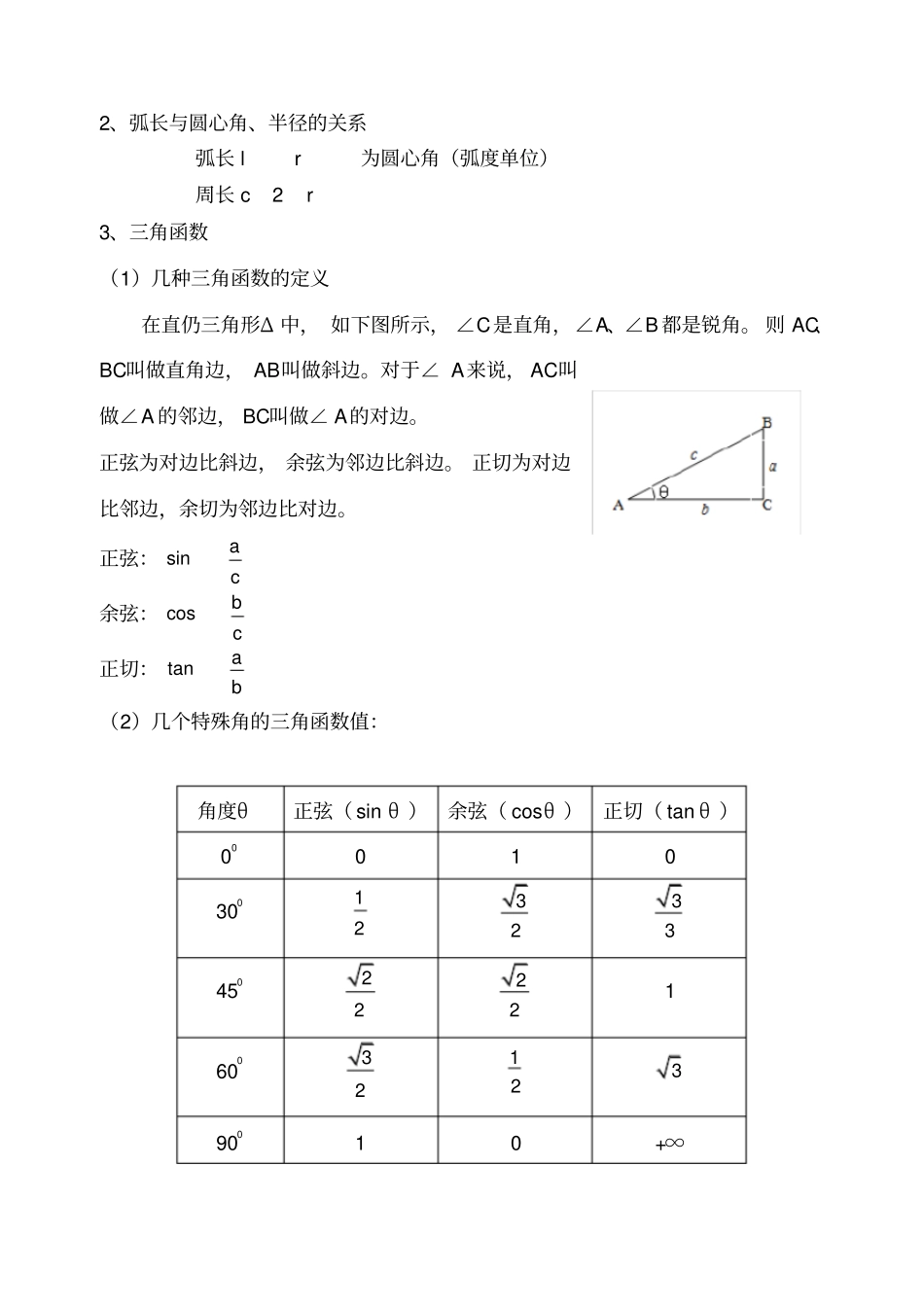
高中物理数学知识准备一、乘法公式1、我们在初中已经学习过了下列一些乘法公式:(1)平方差公式22()()ababab(2)完全平方公式222()2abaabb2222()222abcabcabacbc2、我们还可以通过证明得到下列一些乘法公式:(1)立方和公式2233()()abaabbab(2)立方差公式2233()()abaabbab(3)两数和立方公式33223()33abaababb(4)两数差立方公式33223()33abaababb对上面列出的五个公式,有兴趣的同学可以自己去证明.【课堂例题1】已知4abc,4abbcac,求222abc的值.解:2222()2()8abcabcabbcac.二、直角三角形1、弧度与角度的转换关系1度=π/180弧度(≈弧度)1弧度=180°/π(≈°)【课堂例题3】360°=360×π/180=2π弧度4π/3弧度=4π/3×180°/π=240°2、弧长与圆心角、半径的关系弧长rl为圆心角(弧度单位)周长rc23、三角函数(1)几种三角函数的定义在直仍三角形Δ中,如下图所示,∠C是直角,∠A、∠B都是锐角。则AC、BC叫做直角边,AB叫做斜边。对于∠A来说,AC叫做∠A的邻边,BC叫做∠A的对边。正弦为对边比斜边,余弦为邻边比斜边。正切为对边比邻边,余切为邻边比对边。正弦:sinac余弦:cosbc正切:tanab(2)几个特殊角的三角函数值:角度θ正弦(sinθ)余弦(cosθ)正切(tanθ)00010300123233450222216003212390010+∞180001+∞初中很少遇到的370和530角,在高中物理试题中经常要用到它们。其实这两个角也是大家很熟悉的,还记得“勾3股4弦必5”吧在这个直角三角形中,长为5的边所对的是直角,长为3的边所对的锐角就是370,长为4的边对的角就是530。Sin370=53cos370=54sin530=54cos530=53(3)、当0<α<90°时,正弦与正切函数为增函数,余弦与余切函数为减函数。(4)平方和关系:1cossin22cossintansincoscot(5)正弦、余弦的诱导公式诱导公式一:cos)2sin(sin)2cos(cot)2(tan诱导公式二:cos)2sin(cos-)2sin(cot-)2(tan诱导公式三:sin(+α)=-sinαcos(+α)=-cosαtan(+α)=tanα诱导公式四:sin(-α)=sinαcos(-α)=-cosαtan(-α)=-tanα诱导公式五(k∈Z):sin(2k·+α)=sinαcos(2k·+α)=cosαtan(2k·+α)=tanα诱导公式六:sin(2-α)=sin(-α)=-sinαcos(2-α)=cos(-α)=cosαtan(2-α)=tan(-α)=-tanα【课堂例题4】(2009全国卷Ⅰ文)o585sin的值为(A)22(B)22(C)32(D)32解析:本小题考查诱导公式、特殊角的三角函数值,基础题。2245sin)45180sin()225360sin(585sinoooooo,故选择A.【课堂例题5】(2010年全国理科)记cos(80)k,那么tan100A.21kkB.-21kkC.21kkD.-21kk命题意图:本小题主要考查诱导公式、同角三角函数关系式等三角函数知识,并突出了弦切互化这一转化思想的应用.解析:222sin801cos801cos(80)1k,所以tan100tan802sin801.cos80kk故选择B4、三角形的“四心”三角形是最重要的基本平面图形,很多较复杂的图形问题可以化归为三角形的问题.在三角形中,角平分线、中线、高是三角形中的三种重要线段.重心:三角形的三条中线相交于一点,这个交点称为三角形的重心(如图)。三角形的重心在三角形的内部,恰好是每条中线的三等分点.图图垂心:三角形的三条高所在直线相交于一点,该点称为三角形的垂心。锐角三角形的垂心一定在三角形的内部,直角三角形的垂心为它的直角顶点,钝角三角形的垂心在三角形的外部.(如图)外心:过不共线的三点A、B、C有且只有一个圆,该圆是三角形ABC的外接圆,圆心O为三角形的外心(如图)。三角形的外心到三个顶点的距离相等,是各边的垂直平分线的交点.内心:三角形的三条角平分线相交于一点,是三角形的内心.三角形的内心在三角形的内部,它到三角形的三边的距离相等.(如图)图图【选用例题2】已知ABC的三边长分别为,,BCaACbABc,I为ABC的内心,且I在ABC的边BCACAB、、上的射影分别为D、E、F,求证:2bcaAEAF.证明作ABC的内切圆,则DEF、、分别为内切圆在三边上的切点,,AEAF为圆的从同一点作的两条切线,AEAF,同理,BD=BF,CD=CE.22bcaAFBFAECEBDCDAFAEAFAE即2bcaAEAF.【选用例题3】若三角形的内心与重心为同一点,求证:这个三角形为正...