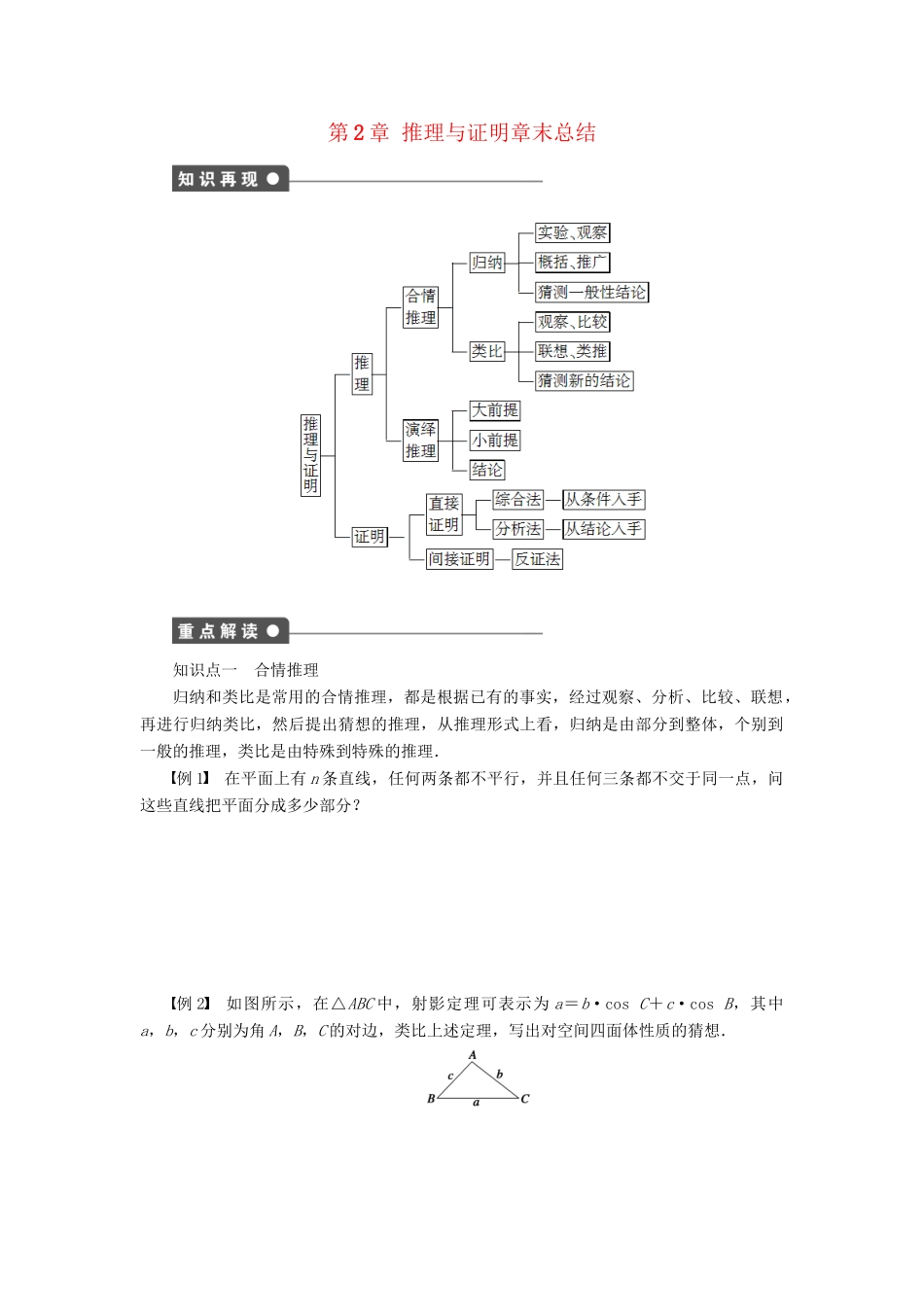
第2章推理与证明章末总结知识点一合情推理归纳和类比是常用的合情推理,都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳类比,然后提出猜想的推理,从推理形式上看,归纳是由部分到整体,个别到一般的推理,类比是由特殊到特殊的推理.例1在平面上有n条直线,任何两条都不平行,并且任何三条都不交于同一点,问这些直线把平面分成多少部分?例2如图所示,在△ABC中,射影定理可表示为a=b·cosC+c·cosB,其中a,b,c分别为角A,B,C的对边,类比上述定理,写出对空间四面体性质的猜想.知识点二演绎推理合情推理的结论不一定正确,有待进一步证明;演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确.从二者在认识事物的过程中所发挥作用的角度考虑,它们又是紧密联系,相辅相成的.合情推理的结论需要演绎推理的验证,而演绎推理的内容一般是通过合情推理获得,合情推理可以为演绎推理提供方向和思路.“”演绎推理的一般模式是三段论.例3已知函数f(x)=+bx,其中a>0,b>0,x∈(0∞,+),确定f(x)的单调区间,并证明在每个单调区间上的增减性.知识点三综合法与分析法综合法和分析法是直接证明中的两种最基本的证明方法,但两种证明方法思路截然相反,分析法既可用于寻找解题思路,也可以是完整的证明过程,分析法和综合法可相互转换,相互渗透,充分利用这一辩证关系,在解题中综合法和分析法联合运用,转换解题思路,增加解题途径.例4已知a,b,c均为正实数,且a+b+c=1,≥求证:8.知识点四反证法反证法是间接证明的一种基本方法,它不去直接证明结论,而是先否定结论,在否定结论的基础上,运用正确的推理,导出矛盾,从而肯定结论的真实性.在证明一些否定性“”“”命题、唯一性命题或含有至多、至少等字句的命题时,正面证明较难,可考虑反证法“”即正难则反.例5已知a,b,c∈(0,1).求证:(1-a)b,(1-b)c,(1-c)a不可能都大于.例6如图所示,已知两直线l∩m=O,l⊂α,m⊂α,l⊄β,m⊄β,α∩β=a.求证:l与m中至少有一条与β相交.章末总结答案重点解读例1解设n条直线分平面为Sn部分,先实验观察特例有如下结果:n123456…Sn247111622…n与Sn之间的关系不太明显,但Sn-Sn-1有如下关系:n123456…Sn247111622…Sn-Sn-123456…观察上表发现如下规律:Sn-Sn-1=n(n=2,3…,).这是因为在n-1条直线后添加第n条直线被原(n-1)条直线截得的n段中的任何一段都将它所在的原平面一分为二,相应地增加n部分,所以Sn=Sn-1+n,即Sn-Sn-1=n.从而S2-S1=2,S3-S2=3,S4-S3=4…,,Sn-Sn-1=n.将上面各式相加有Sn-S1=2+3…++n,∴Sn=S1+2+3…++n=2+2+3…++n=1+.例2解如图所示,在四面体P—ABC中,设S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.我们猜想射影定理类比推理到三维空间,其形式应为:S=S1·cosα+S2·cosβ+S3·cosγ.例3解f(x)的单调区间为和,证明如下:设0
0,0b,∴f(x1)-f(x2)>0,即f(x1)>f(x2),∴f(x)在上是减函数.当x2>x1≥时,则x2-x1>0,x1x2>,,(1-b)c>,(1-c)a>,三式相乘得:(1-a)·a·(1-b)·b·(1-c)·c>,①又因为0