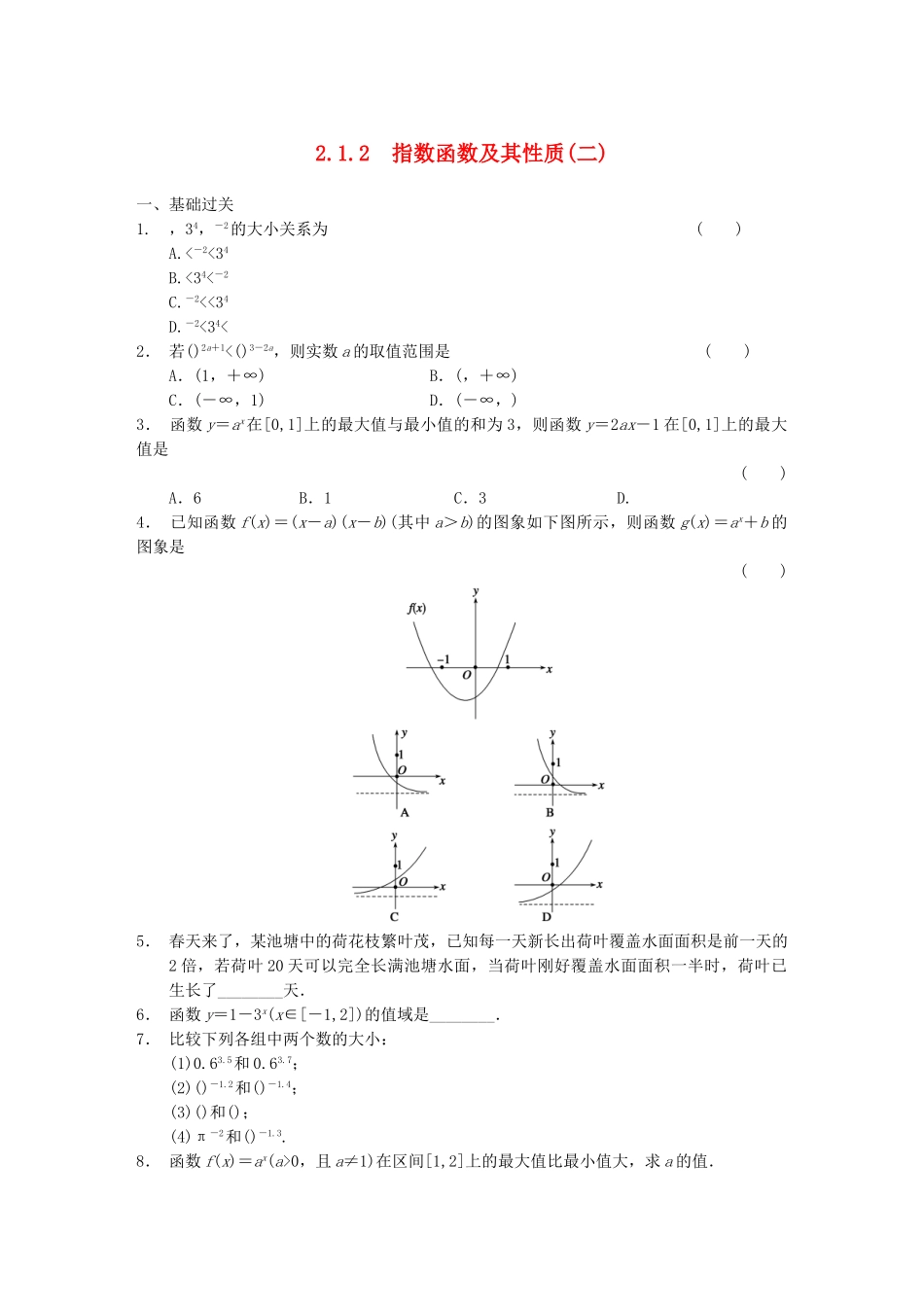
2.1.2指数函数及其性质(二)一、基础过关1.,34,-2的大小关系为()A.<-2<34B.<34<-2C.-2<<34D.-2<34<2.若()2a+1<()3-2a,则实数a的取值范围是()A.(1,+∞)B.(,+∞)C.(-∞,1)D.(-∞,)3.函数y=ax在[0,1]上的最大值与最小值的和为3,则函数y=2ax-1在[0,1]上的最大值是()A.6B.1C.3D.4.已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如下图所示,则函数g(x)=ax+b的图象是()5.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.6.函数y=1-3x(x∈[-1,2])的值域是________.7.比较下列各组中两个数的大小:(1)0.63.5和0.63.7;(2)()-1.2和()-1.4;(3)()和();(4)π-2和()-1.3.8.函数f(x)=ax(a>0,且a≠1)在区间[1,2]上的最大值比最小值大,求a的值.二、能力提升9.已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax-a-x+2(a>0,且a≠1).若g(2)=a,则f(2)等于()A.2B.C.D.a210.设<()b<()a<1,则()A.aa<ab<baB.aa<ba<abC.ab<aa<baD.ab<ba<aa11.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<-的解集是________.12.已知f(x)=(ax-a-x)(a>0且a≠1),讨论f(x)的单调性.三、探究与拓展13.已知定义域为R的函数f(x)=是奇函数.(1)求a,b的值;(2)用定义证明f(x)在(-∞,+∞)上为减函数.(3)若对于任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的范围.答案1.A2.B3.C4.A5.196.[-8,]7.解(1)考查函数y=0.6x.因为0<0.6<1,所以函数y=0.6x在实数集R上是单调递减函数.又因为3.5<3.7,所以0.63.5>0.63.7.(2)考查函数y=()x.因为>1,所以函数y=()x在实数集R上是单调递增函数.又因为-1.2>-1.4,所以()-1.2>()-1.4.(3)考查函数y=()x.因为>1,所以函数y=()x在实数集R上是单调递增函数.又因为<,所以()<().(4)∵π-2=()2<1,()-1.3=31.3>1,∴π-2<()-1.3.8.解(1)若a>1,则f(x)在[1,2]上递增,∴a2-a=,即a=或a=0(舍去).(2)若0
0,∴当a>1时,ax10,∴f(x1)-f(x2)<0,f(x1)ax2,<0,∴f(x1)-f(x2)<0,f(x1)