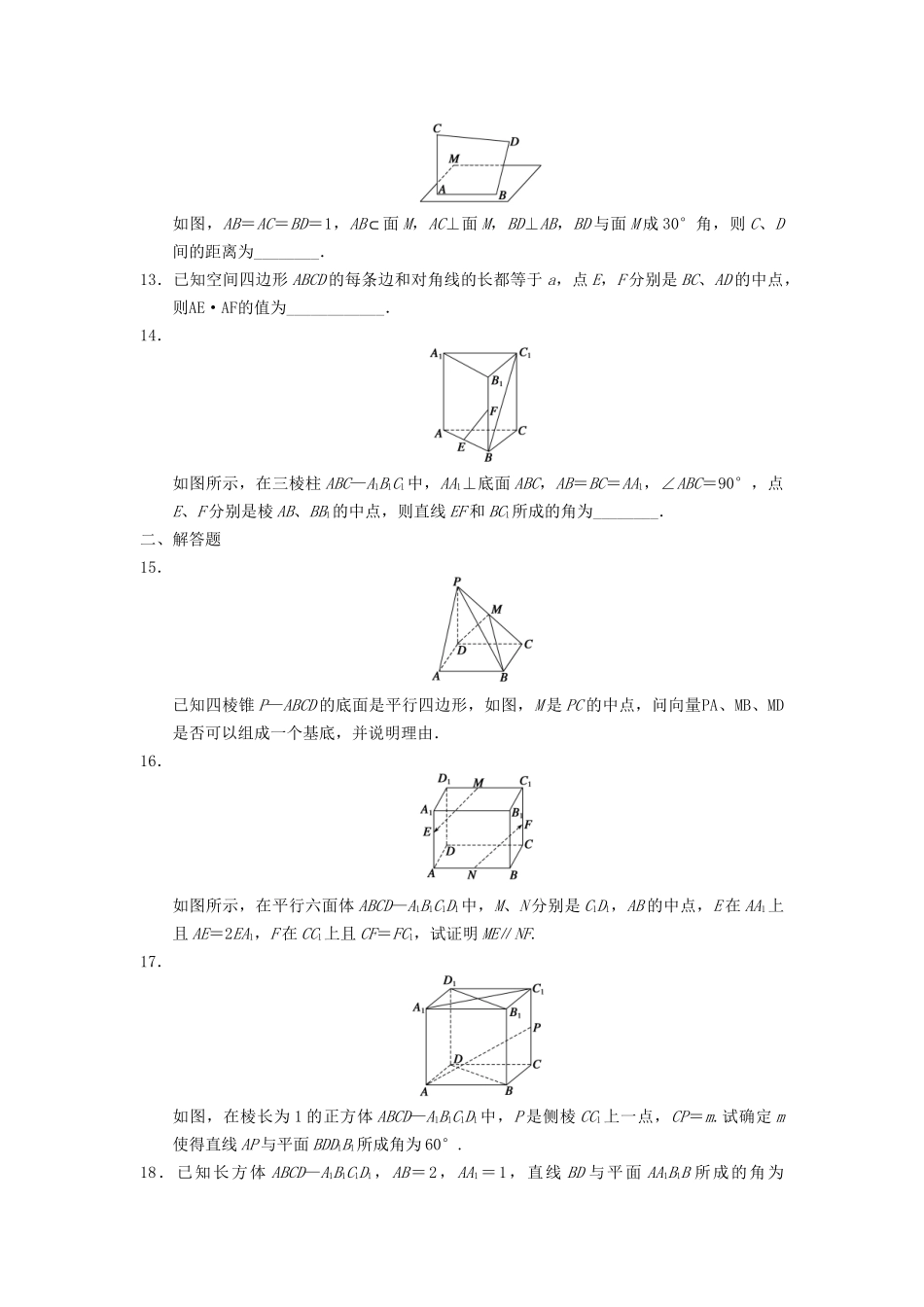
章末检测一、填空题1.已知平面α和平面β的法向量分别为m=(3,1,-5),n=(-6,-2,10),则平面α、β的位置关系为________.2.已知向量a=(0,2,1),b=(-1,1,-2),则a与b的夹角为________.3.如图,在平行六面体ABCD—A1B1C1D1中,已知AB=a,AD=b,AA1=c,则用向量a,b,c可表示向量BD1=______________.4.已知P和不共线三点A,B,C四点共面且对于空间任一点O,都有OP=2OA+OB+λOC,则λ=________.5.已知A(2,1,0),点B在平面xOz内,若直线AB的方向向量是(3,-1,2),则点B的坐标是________.6.平面α的法向量为m=(1,0,-1),平面β的法向量为n=(0,-1,1),则平面α与平面β所成二面角的大小为______.7.若平面α的法向量为n,直线l的方向向量为a,直线l与平面α的夹角为θ,则下列关系式成立的是________.(填序号)①cosθ=②cosθ=③sinθ=④sinθ=8.设A、B、C、D是空间不共面的四点,且满足AB·AC=0,AC·AD=0,AB·AD=0,则△BCD是________三角形.(“”“”“”填锐角、直角、钝角)9.在以下命题中,不正确的个数为________.①|a|-|b|=|a+b|是a,b共线的充要条件;②对a∥b,则存在唯一的实数λ,使a=λb;③对空间任意一点O和不共线的三点A,B,C,若OP=2OA-2OB-OC,则P,A,B,C四点共面;④|(a·b)·c|=|a|·|b|·|c|.10.法向量为n=(1,-1,1)的平面α过点M(1,2,-1),则平面α上任意一点P的坐标(x,y,z)满足的方程为____________.11.设E,F是正方体AC1的棱AB和D1C1的中点,在正方体的12条面对角线中,与截面A1ECF成60°角的对角线的数目是________.12.如图,AB=AC=BD=1,AB⊂面M,AC⊥面M,BD⊥AB,BD与面M成30°角,则C、D间的距离为________.13.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC、AD的中点,则AE·AF的值为____________.14.如图所示,在三棱柱ABC—A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角为________.二、解答题15.已知四棱锥P—ABCD的底面是平行四边形,如图,M是PC的中点,问向量PA、MB、MD是否可以组成一个基底,并说明理由.16.如图所示,在平行六面体ABCD—A1B1C1D1中,M、N分别是C1D1,AB的中点,E在AA1上且AE=2EA1,F在CC1上且CF=FC1,试证明ME∥NF.17.如图,在棱长为1的正方体ABCD—A1B1C1D1中,P是侧棱CC1上一点,CP=m.试确定m使得直线AP与平面BDD1B1所成角为60°.18.已知长方体ABCD—A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,F为A1B1的中点.求二面角A—BF—D的余弦值.19.如图,在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2,M,N分别为PB,PD的中点.(1)证明:MN∥平面ABCD;(2)过点A作AQ⊥PC,垂足为点Q,求二面角A-MN-Q的平面角的余弦值.20.如图所示,在正方体ABCD—A1B1C1D1中,E是棱DD1的中点.(1)求直线BE和平面ABB1A1所成的角的正弦值;(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.答案1.α∥β2.90°3.-a+b+c4.-25.(5,0,2)6.60°或120°7.④8.锐角9.410.x-y+z+2=011.412.13.a214.60°15.解PA、MB、MD不可以组成一个基底,理由如下:连结AC、BD相交于点O, ABCD是平行四边形,∴O是AC、BD的中点,在△BDM中,MO=(MD+MB),在△PAC中,M是PC的中点,O是AC的中点,则MO=PA,即PA=MD+MB,即PA与MD、MB共面.∴PA、MB、MD不可以组成一个基底.16.证明由平行六面体的性质ME=MD1+D1A1+A1E=C1D1-AD+A1A=-AB-AD-AA1,NF=NB+BC+CF=AB+AD+CC1=AB+AD+AA1,∴ME=-NF,又M,E,N,F不共线,∴ME∥NF.17.解建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1).则BD=(-1,-1,0),BB1=(0,0,1),AP=(-1,1,m),AC=(-1,1,0).又由AC·BD=0,AC·BB1=0知,AC为平面BB1D1D的一个法向量.设AP与平面BB1D1D所成的角为θ,则sinθ=|cos〈AP,AC〉|==依题意得=sin60°=,解得m=.故当m=时,直线AP与...