函数及其表示VIP免费

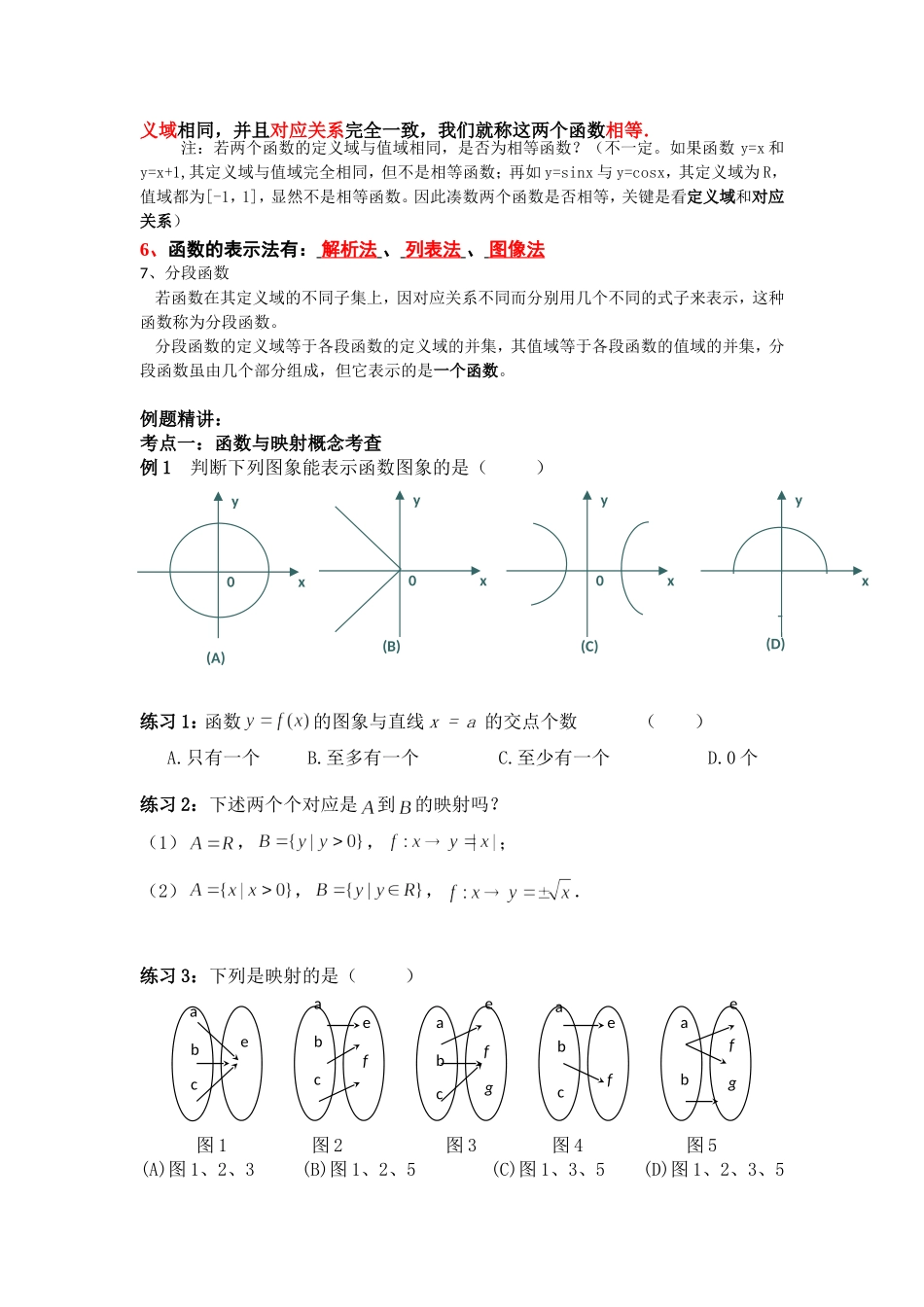
函数及其表示基础知识1、函数与映射的概念函数映射两集合设AB、是两个非空数集设AB、是两个非空集合对应关系:fAB如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数()fx和它对应。如果按某一个确定的对应关系f，使对于集合A中的任意一个元素x，在集合B中都有唯一确定的元素y与之对应。名称称:fAB为从集合A到集合B的一个函数称:fAB为从集合A到集合B的一个映射记法()yfx，xA对应:fAB是一个映射注：函数与映射的区别：函数是特殊的映射，二者区别在于映射定义中的两个集合是非空集合，可以不是数集，而函数中的两个集合必须是非空数集。2.函数的定义域与值域在函数Axxfy),(中，x叫做自变量，x的取值范围A叫做)(xfy的定义域；与x的值相对应的y值叫做函数值，函数值的集合Axxf)(称为函数)(xfy的值域.显然，值域是集合B的子集。温馨提示：(1)A、B都是非空数集，因此定义域(或值域)为空集的函数不存在．(2)函数关系的判断要注意“每一个”、“都有”、“唯一”等关键词．(3)注意f(x)与f(a)的区别，f(a)表示当x＝a时的函数值，是一个常量；而f(x)是关于x的函数，一般情况下是一个变量，f(a)是f(x)的一个特殊值．（4）y=f(x)仅仅是函数符号。3、函数的构成要素：定义域、对应关系和值域4、区间的概念及表示法设是两个实数，且，满足的实数的集合叫做闭区间，记做；满足的实数的集合叫做开区间，记做；满足，或的实数的集合叫做半开半闭区间，分别记做，；满足的实数的集合分别记做。注意：对于集合与区间，前者可以大于或等于，而后者必须。5、相等函数：由于值域是由定义域和对应关系决定的，所以，如果两个函数的定义域相同，并且对应关系完全一致，我们就称这两个函数相等．注：若两个函数的定义域与值域相同，是否为相等函数？（不一定。如果函数y=x和y=x+1,其定义域与值域完全相同，但不是相等函数；再如y=sinx与y=cosx，其定义域为R，值域都为[-1，1]，显然不是相等函数。因此凑数两个函数是否相等，关键是看定义域和对应关系）6、函数的表示法有：解析法、列表法、图像法7、分段函数若函数在其定义域的不同子集上，因对应关系不同而分别用几个不同的式子来表示，这种函数称为分段函数。分段函数的定义域等于各段函数的定义域的并集，其值域等于各段函数的值域的并集，分段函数虽由几个部分组成，但它表示的是一个函数。例题精讲：考点一：函数与映射概念考查例1判断下列图象能表示函数图象的是（）练习1：函数的图象与直线x=a的交点个数（）A.只有一个B.至多有一个C.至少有一个D.0个练习2：下述两个个对应是到的映射吗？（1），，；（2），，．练习3：下列是映射的是（）图1图2图3图4图5(A)图1、2、3(B)图1、2、5(C)图1、3、5(D)图1、2、3、5xy0(A)xy0(B)xy0(D)xy0(C)abceabcefabcefgabcefabefg函数相等：如果两个函数的定义域相同，并且对应关系完全一致.例2指出下列各函数中，哪个与函数是同一个函数：（1）；（2）；（3）．练习1：判定下列各组函数是否为同一个函数：（1），；（2），练习2：试判断以下各组函数是否表示同一函数？（1）2)(xxf，33)(xxg；（2）xxxf)(，;01,01)(xxxg（3）xxf)(1x，xxxg2)(；（4）12)(2xxxf，12)(2tttg（5）1212)(nnxxf，1212)()(nnxxg（n∈N*）；考点二：函数定义域题型1：求有解析式的函数的定义域（1）若f(x)为整式，则其定义域为实数集R（2）若f(x)是分式，则其定义域是使分母不等于0的实数的集合（3）若f(x)是偶次根式，则其定义域是使根号内的式子大于或等于0的实数的集合。（4）若f(x)是由几个部分的数学式子构成的，那么函数定义域是使各部分都有意义的实数的集合，即交集。（5）例１求下列函数的定义域：（１）；（２）．例2设，求，，，．练习1：函数的定义域为（）A．B．C．D．练习2：函数的定义域是（）A.B.C.D.题型2：求复合函数和抽象函数的定义域1、复合函数的定义如果是的函数，又是的函数，即，，那么关于的函数叫做函数（外函数）和（内函数）的复合函数，其中是中间变量，自变量为函数值为。例如：函数是由和...