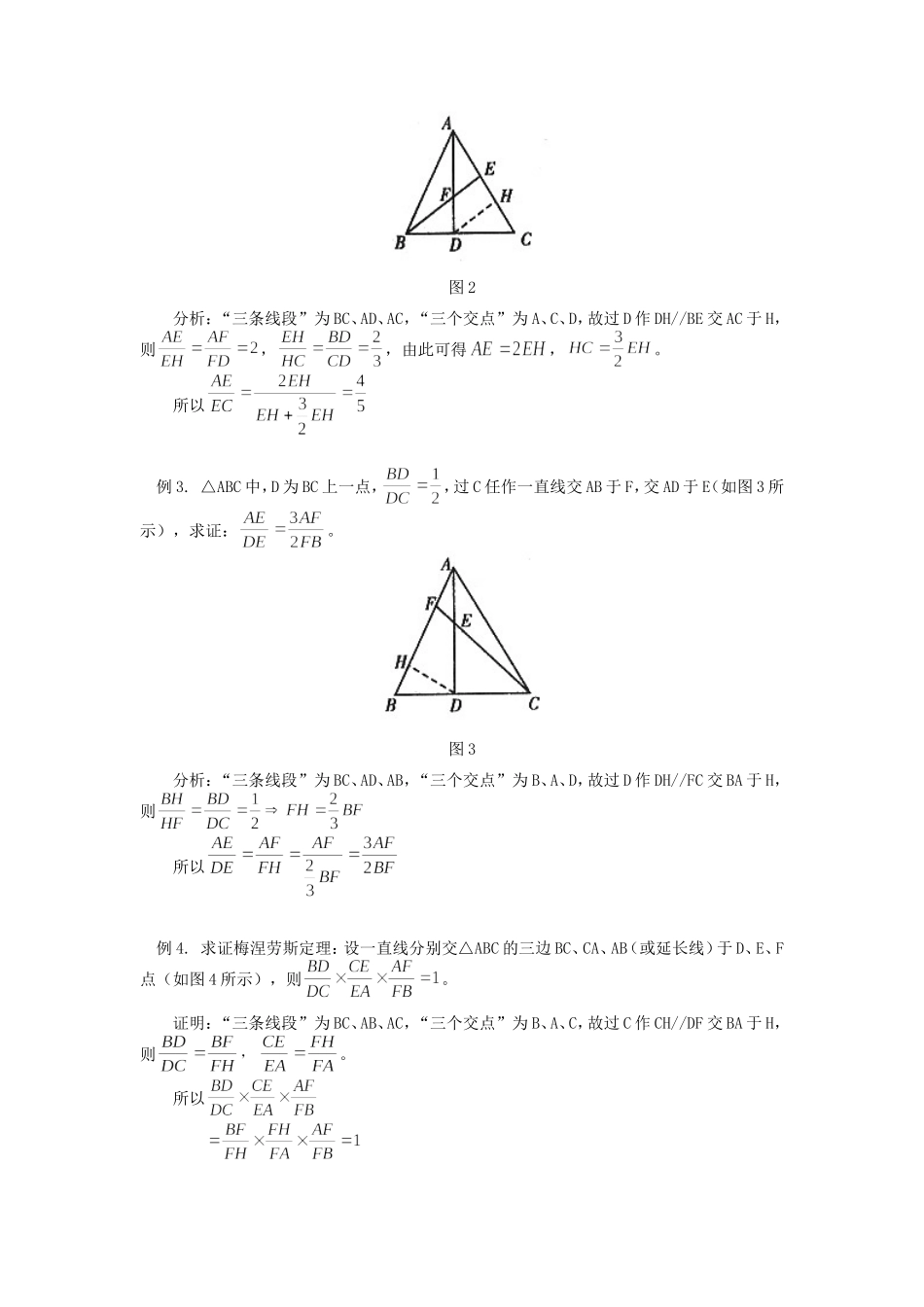
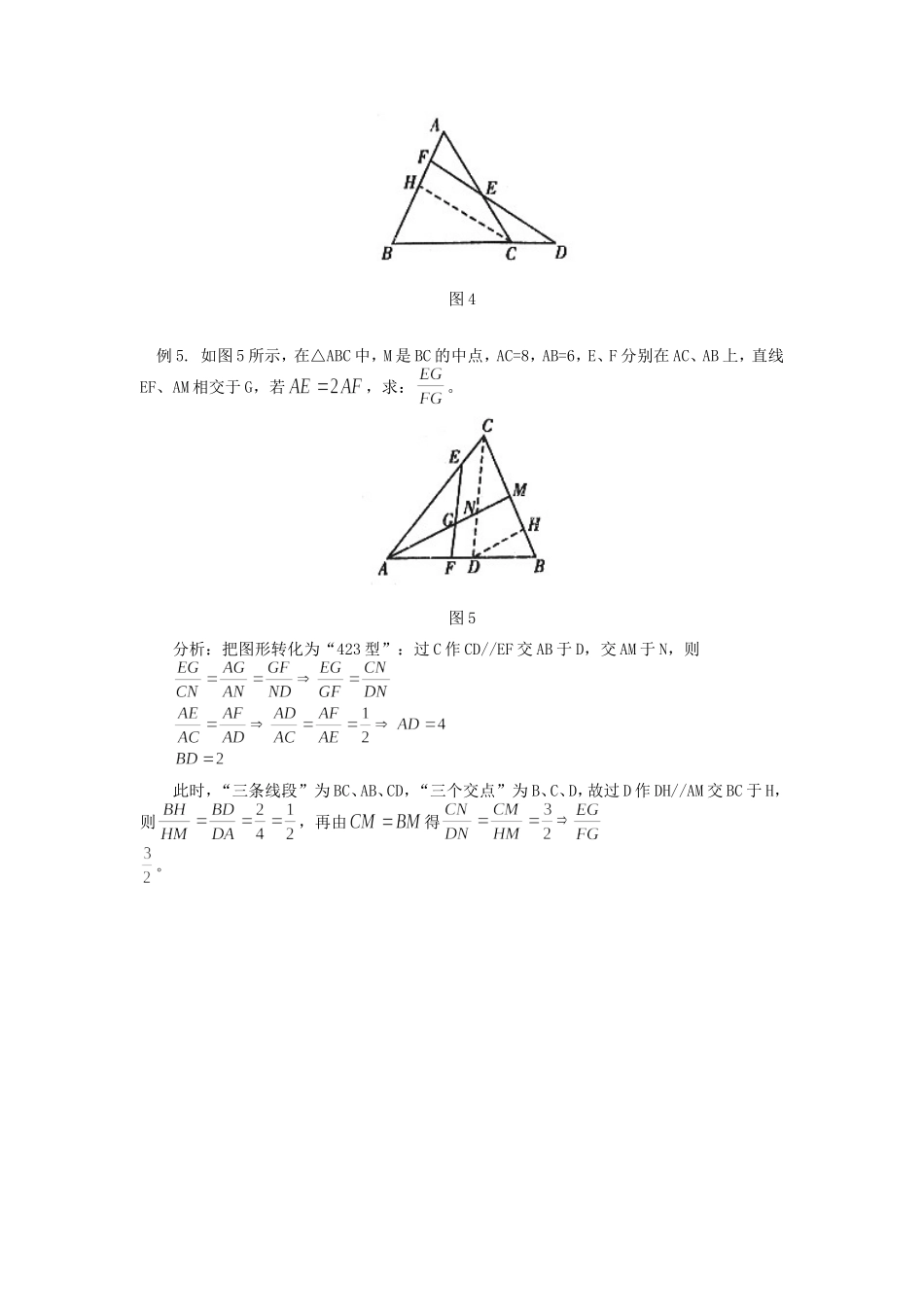
初中数学“423型”题的解题思路高其校如图所示,△ABC中,D在BC上,E在AC上,AD、BE相交于F,则图中有4个独立的比,若已知其中2个比,则必可求出第3个比,在此简称“423型”题。此题型是相似三角形中的常见题型,但很多学生感到难以下手,笔者通过多年教学,总结出一条解题路子,供读者参考。首先找到已知的2个比和要求的第3个比所在的三条线段,此三条线段两两相交,可得三个交点,这三个交点中必有D、E、F之一或之二。若有F,则过F作一线段的平行线,使其与上三条线段之一相交,若没有F,则过D或E作一线段的平行线使其与上三条线段之一相交,然后利用“平行线分线段成比例定理”即可求解。例1.已知:△ABC中,D在BC上,E在AC上,AD、BE相交于F(如图1所示),,求。图1分析:“三条线段”为BC、AD、BE,“三个交点”为B、F、D。故过F作FH//AC交BC于H,则设再由得所以例2.在上例中,若已知不变(如图2所示),求。图2分析:“三条线段”为BC、AD、AC,“三个交点”为A、C、D,故过D作DH//BE交AC于H,则,,由此可得,。所以例3.△ABC中,D为BC上一点,,过C任作一直线交AB于F,交AD于E(如图3所示),求证:。图3分析:“三条线段”为BC、AD、AB,“三个交点”为B、A、D,故过D作DH//FC交BA于H,则所以例4.求证梅涅劳斯定理:设一直线分别交△ABC的三边BC、CA、AB(或延长线)于D、E、F点(如图4所示),则。证明:“三条线段”为BC、AB、AC,“三个交点”为B、A、C,故过C作CH//DF交BA于H,则。所以图4例5.如图5所示,在△ABC中,M是BC的中点,AC=8,AB=6,E、F分别在AC、AB上,直线EF、AM相交于G,若,求:。图5分析:把图形转化为“423型”:过C作CD//EF交AB于D,交AM于N,则此时,“三条线段”为BC、AB、CD,“三个交点”为B、C、D,故过D作DH//AM交BC于H,则,再由得。